
事業価値を計ってみよう その2
それでは引き続きやっていきましょう。前回の記事では
フリーキャッシュフローの考え方を確認しました。
今回は将来のキャッシュフローを現在価値に換算するため、
WACCから見ていきます。
WACCとは
加重平均資本コスト(Weighted Average Cost of Capital)のことで、ワックと読みます。
計算式はこちら。

要素を1つずつ見ていきます。
・負債コスト
企業が行った資金調達のうち、債権者から調達した負債にかかるコストのこと。つまり、借金に対する利息(借入金利)です。
支払利息分は税金の控除が受けられるので、税引き後の値段として計算するために(1 - 実効税率)が掛かっています。
負債コストは、債権者側から見れば債権の利回りです。
・株主資本コスト
負債コストの対として考えると、株主資本コストは株主の期待する利回り(配当+キャピタルゲイン)と考えられます。
株主の利回りが会社から見るとコストとなる部分は少し違和感があるかもしれませんが、一旦これで進めます。
WACCは会社が資本を調達するのにかかるコスト(資本コスト)を、債権と株式の2つの調達方法それぞれで計算して加重平均をしたもの、と理解してもらえればOKです。
負債コスト(借入金利)は調べれば分かりそうですが、株主資本コストはどのように計算すればよいのでしょうか。
CAPMとは
株主資本コストを求める最もポピュラーな理論であるCAPM(Capital Asset Pricing Model)を見てみます。キャップエムと読みます。

株主資本コストは前述した通り、株主が期待する利回りだと考えてください。
リスクフリー・レートは無リスク資産の利回りです。通常は米国の10年債など、限りなくリスクが低い資産の利回りを使用します。
ファイナンス理論では、無リスク資産以上リターンを得るためにはリスクを取る必要があると考えます。ここで言うリスクはリターンのばらつき(ボラティリティ)です。
株式は国債に比べてリスクの高い金融資産と考えられています。
株式などのリスク資産を購入することで得られる追加リターン(無リスク資産とのリターンの差)をリスク・プレミアムと言います。
マーケットリスク・プレミアムとはTOPIXやS&P500のような株価指数のリスク・プレミアムで、これに係数βを掛けることで個別株のリスク・プレミアムを見積もります。
βは過去のデータから統計的に計算される係数で、計算してくれるサイトもあります。

これで将来のキャッシュフローを現在価値で割り引き、会社の事業価値を見積もるための役者は揃いました。
最後に、「現在価値に割り引く」という考え方を確認しておきます。
現在価値に割り引く
年に10万円の利息を永久に受け取れる債権を考えます。安定した収入源として年利回り3%を期待して購入した国債と仮定し、この債権の現在価値を考えます。
1年後に受け取る10万円は、3%の利回りで割り引いて9.7万円(10 ÷ 1.03 = 9.7)です。
2年後に受け取る10万円は、9.4万円(10 ÷ 1.03 ÷ 1.03 = 9.4)です。
このまま将来に受け取る利息の合計は無限等比級数の和の考え方で計算できます。
せっかくなので高校生の気持ちになって計算してみます。

両辺に期待利回り(1.03%)を掛けます。

②から①を引くと、②の右辺の2項以降がキレイに消え、
式を整えると以下になります。

というわけで、この場合の将来受け取れる利息の合計の現在価値は333万円
ということになります。これはそのままこの債権の現在価値と言い換えられます。
現在の資産に期待する利回りを掛けると将来の資産価値を見積もれることは理解できると思います。
現在価値に割り引くとは、その逆の計算をやっていることになります。
事業価値
WACCは会社が資産調達するのにかかるコストであり、資金提供者目線では期待する利回りです。
企業の将来のキャッシュフローが一定の成長率で伸びていくと仮定すると、上記の現在価値の式は以下のように一般化できます。
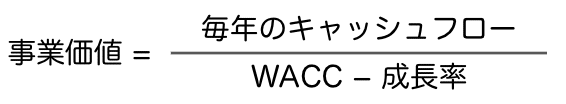
興味ある方は無限等比級数の和の部分に戻って、成長率を公比に組み込んだ上で再度計算をしてみてください。上の式が導かれるはずです。
おわりに
ファイナンス理論における事業価値の計算方法を見ていきました。
マーケットリスク・プレミアムやβ、キャッシュフローの成長率など、かなり不安定な仮定を前提として計算されていることが分かります。
これらの計算で得られる値の正確性については疑問が残ると思いますが、事業価値というざっくりとした概念を一般化し、定量的に比較できるものに落とし込んでいることにファイナンス理論の価値があるように思われます。
次回は実際の企業の事業価値を計算してみます。
疑問点、誤りの指摘などありましたらコメントいただければ幸いです。
