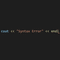ABC256感想など

ABC256に参加した感想と簡単な解説です。
A~Dの４完でした。

A問題

2のN乗を計算します。
ABC256にふさわしい問題でしたね。
2のN乗は1 << Nで求められます。
計算の優先順位に注意しましょう

#include <bits/stdc++.h>
using namespace std;
int main(){
  int N;
  cout << (1 << N) << endl;
}

print(1 << int(input()))

B問題

シミュレーションすればいい問題。
めんどいですが、愚直にやりましょう。

#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<(n);i++)
using namespace std;
int main() {
  int N;
  cin >> N;
  vector<int> A(N);
  rep(i, N) cin >> A[i];
  vector<int> P(4);
  int ans = 0;
  rep(i, N) {
    P[0]++;
    for (int j = 3; j >= 0; j--) {
      if (j + A[i] <= 3) {
        P[j + A[i]] = P[j];
      } else {
        ans += P[j];
      }
      P[j] = 0;
    }
  }
  cout<<ans<<endl;
}

C問題

全探索です！！
僕は初回の参加(ABC241)が全探索だったことで、印象が強かったので方針がすぐに立ちました。
入力≤30なので全探索できそうですよね。
僕は横に2つずつ全探索→残りの一つを出す　を縦に３つやっているので
$${O(N^6)}$$ で解きました。
$${30^6}$$≒$${7 \times 10^8}$$なので、ナイーブなコードでは通りません。
そもそも横の二つを揃えたところでありえない数のところはcontinue;してあげれば定数倍が軽いので通ります。
提出コードはこれで行けるやろ！くらいの気持ちで投げたので無駄が多いです。
ちなみに、左上の４つのみを全探索することで残りが決まるので、そちらを使った方がいいですね。

#include <bits/stdc++.h>
using namespace std;
#define REP(i, a, b) for(int i=a;i<(b);i++)
int main() {
  vector<int> h(3), w(3);
  for (int i = 0; i < 3; i++) cin >> h[i];
  for (int i = 0; i < 3; i++) cin >> w[i];
  int ans{};
  REP(a, 1, h[0]) REP(b, 1, h[0]) {  //横一列目
    int c = h[0] - a - b;
    if (1 > c) continue;
    REP(d, 1, h[1]) REP(e, 1, h[1]) {  //横二列目
      int f = h[1] - d - e;
      if (1 > f) continue;
      REP(g, 1, h[2]) REP(h2, 1, h[2]) {
        int i = h[2] - g - h2;
        if (1 > i) continue;
        if (a + d + g != w[0] || b + e + h2 != w[1] || c + f + i != w[2])
          continue;
        ans++;
      }
    }
  }
  cout << ans << endl;
}

D問題

Cより解きやすい人も多かったかな？
区間の被る部分をごりごりしてもいいですが、区間の始まりと終わりを使っていもす法を使うと簡単です。
+1,-1して累積和を取っておきます。
区間が連続しているかをboolで持って左から順にみていくと0でないときは区間内なので、0→1以上と1以上→0となる部分が求める区間になります

#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<(n);i++)
#define REP(i,a,b) for(int i=a;i<b;i++)
#define ALL(x) x.begin(),x.end()
using namespace std;
int main() {
  int N;
  cin >> N;
  vector<pair<int,int>> S(N);
  ll mx{};
  rep(i, N) {
    cin >> S[i].first >> S[i].second;
    chmax(mx, S[i].second);
  }
  vector<int> B(mx + 1);
  for (auto &[a, b] : S) {
    B[a]++;
    B[b]--;
  }
  vector<pair<int,int>> ans;
  bool a{};
  REP(i, 1, mx + 1) B[i] += B[i - 1];
  int buf{};
  REP(i, 1, mx + 1) {
    if (B[i] > 0) {
      if (!a) {
        buf = i;
        a = 1;
      }
    } else {
      if (a) {
        ans.push_back({buf, i});
        buf = 0;
        a = 0;
      }
    }
  }
  sort(ALL(ans));
  for (auto &[a, b] : ans) cout << a << " " << b << endl;

解けなかったE問題

Dまでが割とすぐ(40分弱)終わったので考察で椅子を温めました。
グラフで考えるといいのはすぐ出ました。
まず考えたこと→最小全域木を作る
クラスカル法もプリム法もやったことがなかったので調べながらやりました。
ただ、０の辺の扱いをどうしてよいのかわからず…
次→閉路のあるところだけでよくない？
解説と同じ方針(？)です。だいぶここまでに時間がかかっていたので通しきれませんでした。
閉路のないところはコスト０でつなげられるので、閉路になっているところのうち、一番不満度の低い人を使ってあげればいいです。
問題は実装で、みんな大好きDFSをしようと思ったのですが、実装が重く、時間が足りませんでした。
解説を読んで、サイクルなら有向グラフなのでぐるぐるしてるだけだから、ufで閉路検出→ぐるぐるしてコストを見る
をすればよかったんですね…

まとめ

今回はいい感じに解けて楽しかった！
Eも練習しなきゃ！
241のCも楽しいから解いてみて！
(コミュ障はどうやったら直りますか？)
次も緑パフォ出す！