
書記が数学やるだけ#856 ホモロジー群の計算
ホモロジー群の具体的な計算をいくつか行う。
問題

解答
まずは木構造のグラフについて,0次ホモロジー群のみZと同型,あとは0である。0次ホモロジー群については,グラフが連結であることからもわかる。

次にブーケ構造のグラフについて,0次ホモロジー群はZと同型,1次ホモロジー群はZの直和と同型,ほかは0である。なお,ブーケの個数が1次ホモロジー群におけるZの直和の個数に対応する。
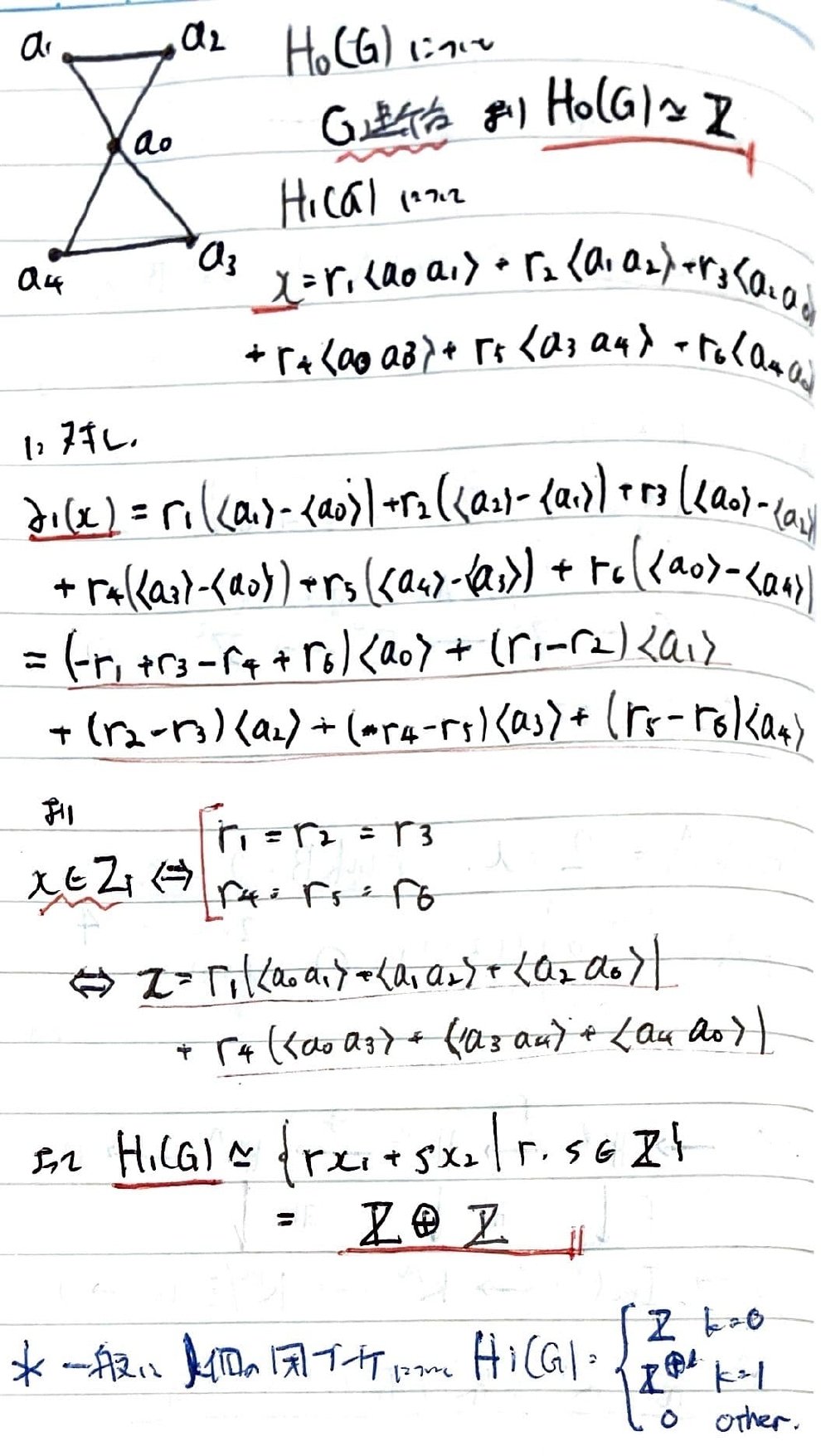
次に連結でないグラフを考える。この場合,0次ホモロジー群は連結要素の個数が直和の個数に対応する。

1次ホモロジー群について,閉路の個数が直和の個数に対応する。

2次元曲面の例として球面を扱う。定義通り計算すると,0次ホモロジー群はZと同型である。

1次ホモロジー群は0と同型となる。

2次ホモロジー群はZと同型となる。

本記事のもくじはこちら:

