
書記が数学やるだけ#675 波動方程式のダランベール解
波動方程式の解法について改めて見ていく。
問題

説明
波動方程式は双曲型偏微分方程式の代表例である。

波動方程式の導出は以前に行った:

解答
波動方程式の解導出は覚えておく必要がある。

初速が0の場合のxt平面を示す。

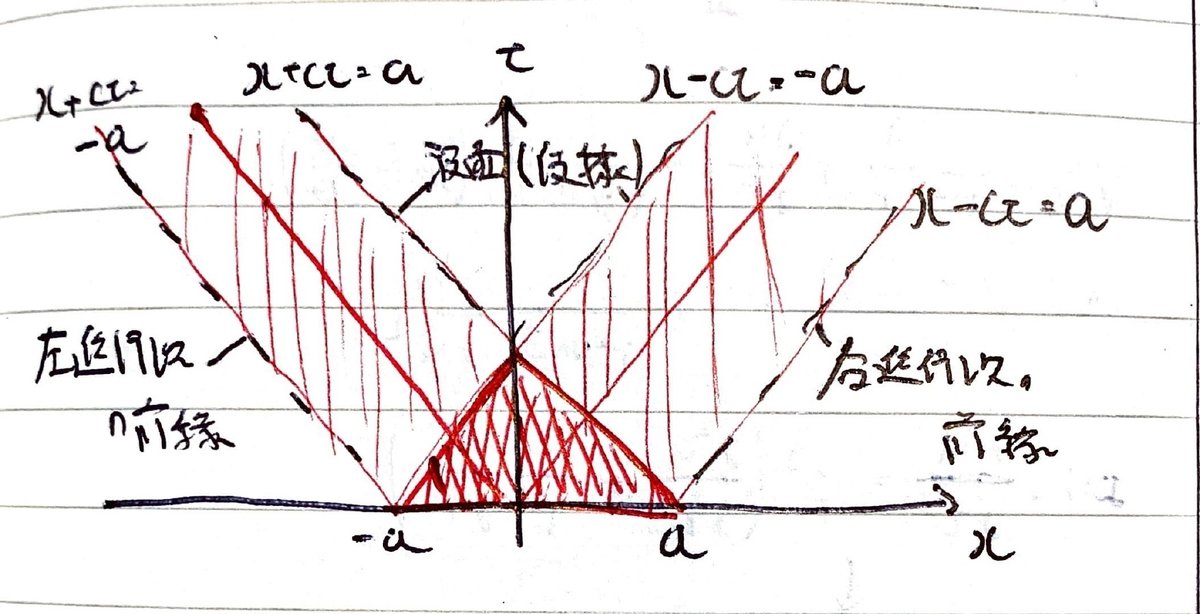
初期位置が0の場合。

本記事のもくじはこちら:

波動方程式の解法について改めて見ていく。

波動方程式は双曲型偏微分方程式の代表例である。

波動方程式の導出は以前に行った:

波動方程式の解導出は覚えておく必要がある。

初速が0の場合のxt平面を示す。


初期位置が0の場合。

本記事のもくじはこちら: