
書記が数学やるだけ#788 自然演繹の規則-1
今回から自然演繹による証明を扱っていく,まずは記法に慣れるところから。
問題
記法の練習は2回に分けて行う。

説明
自然演繹は,主にゲルハルト・ゲンツェンにより定式化された形式で,公理を極力少なくして推論規則で話を進めるのが特徴である。
例えば,ジョン・レモンが開発した体系 L は証明の構文規則に関する以下の9つの基本的規則だけを持つ。

以下,NK(古典論理)の推論規則を紹介する。
自然演繹では,線の上に並んだ前提から線の下にある結論を導くことを図で示していく。
まずモーダスポネンスについて,「P ならば Q である。P である。従って,Q である。」ことを示している。Qが導かれたときには,前提にあった→が結論から除去される。

次に→導入について,ここで…は未完成の証明であり,ここに規則を埋めることで仮定Pまで繋げていく。

論理積の除去について,「PかつQ」からPとQの2つを示すことができる。

論理積の導入について,PとQの両方が示れば「PかつQ」を示すことができる。

論理和の除去は,「PまたはR」が成り立つとき,「P→Q」と「R→Q」の2つの場合が示すことができれば,PとRのどちらかが成り立つかによらずQが成り立つことが言える。

論理和の導入では,PかQのいずれかが示せれば「PまたはQ」が示せる。

解答
証明を書く際はは下から辿っていく。まず「→」が無くなるように,→の導入規則を立てる,ここでAは仮定として上段で示す。次に仮定の右側が出るように→の除去規則を立てる。最後に→の除去規則を立てれば,全ての前提に帰着できる。

本問は→の除去規則のみで構築できる。簡単な命題から複雑な命題へと組み立てるようにするとうまくいく。

次に論理積について,論理積の除去規則により増やしつつも,→の除去規則を用いてAを引き出す。

初手は導入規則により単純化する,その後AとCに分けて個別に「AかつB」が前提となるようにする。

本問は仮定が全て取り除かれたケースで,これを定理という。ここでは論理和と論理積の規則を用いる。

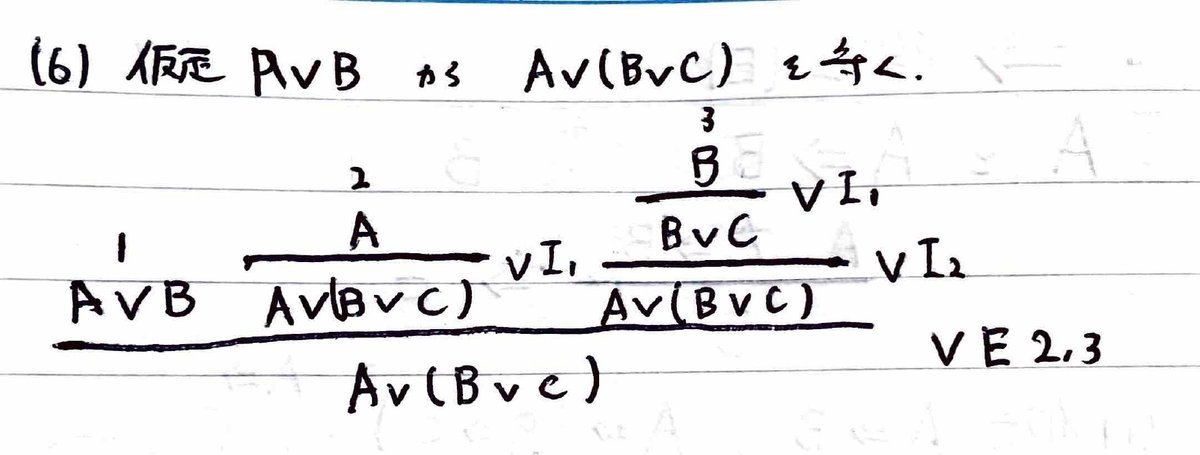
論理和の除去について,仮定より「AまたはB」が成り立ち,場合分けしてAとBの両方が成り立つので,「Aまたは(BまたはC)」を示すことができる。
本記事のもくじはこちら:
学習に必要な本を買います。一覧→ https://www.amazon.co.jp/hz/wishlist/ls/1XI8RCAQIKR94?ref_=wl_share
