書記が数学やるだけ#349 2変数関数のテイラー展開，2重数列の極限の順序

テイラー展開を多変数関数に拡張する。

問題

説明

テイラー展開の多変数への拡張。

中でも2次近似は線形代数とも連携する。

このことから，勾配とヘッセ行列から極値を求めることができる。

数列の多変数への拡張として，2重数列を考える。

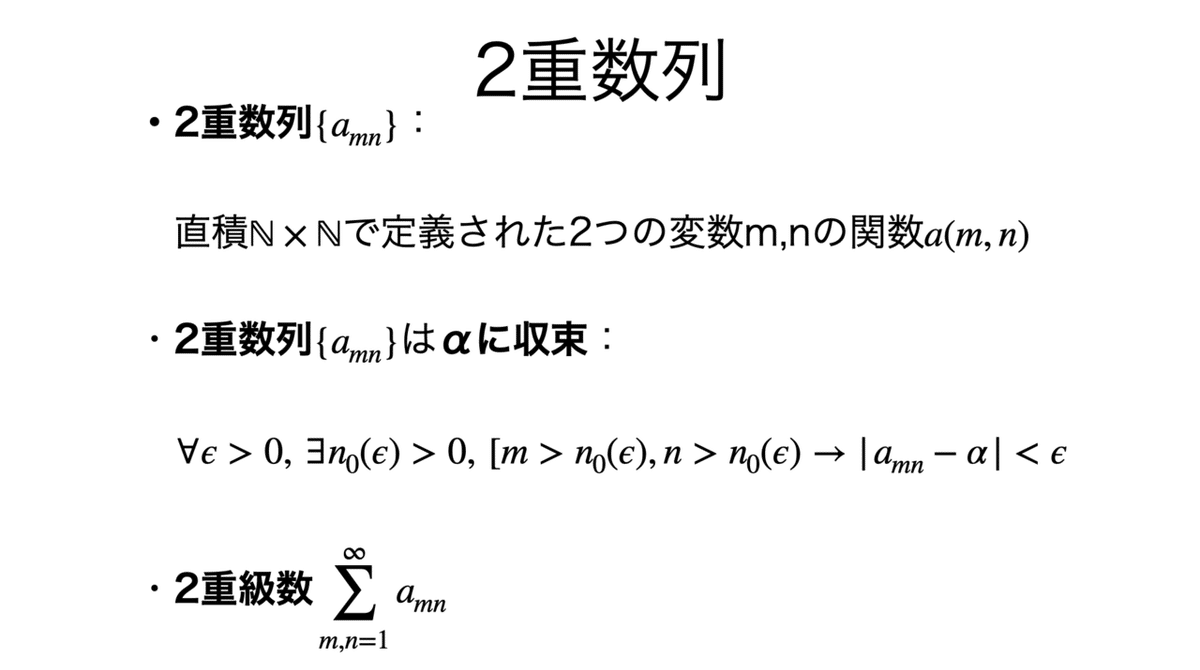
2重数列の極限の順序は，mに対して一様収束であれば入れ替え可能である。

解答

1変数の場合：

このあたりは，線形代数でも出てくる問題である。

2重数列の極限の順序について証明をしておく。

これを積分と極限の順序に適用する。

本記事のもくじはこちら：