書記が数学やるだけ#836 極と極線，調和点列

極と極線および調和点列について一般化を行う。

問題

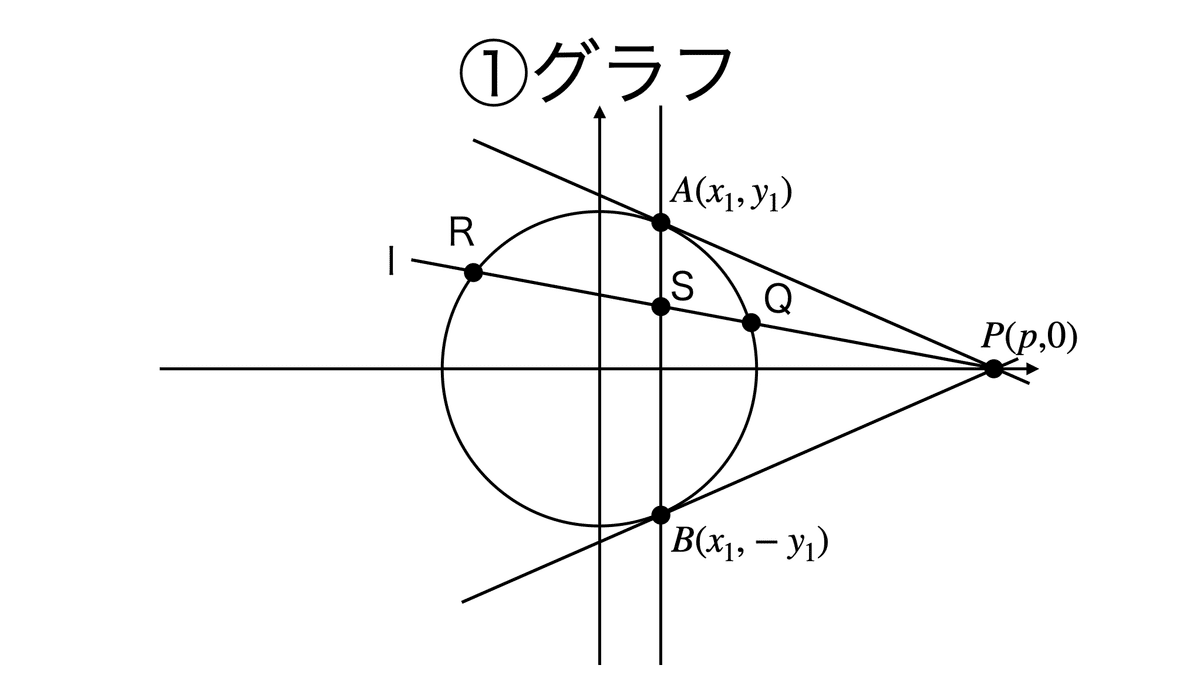
①は円について極と極線および調和点列を考える，2006年の神戸大では放物線が出題された。

説明

二次曲線に2本の接線を引き，接線の交点を極，接点同士を結んだ直線を極線という。

複比が-1の場合を，特に調和共役という。

解答

極線の方程式を導出するには，接線の方程式を考えればよい。

本題は以下の等式で，以下の場合においてベクトル方程式を考える。

式変形により調和点列であることがわかる。

以上のことを二次曲線に一般化するために，接線・極線の式を導出しておく。

交点の斉次座標から複比が-1であることが求められ，調和点列であることが示せた。

本記事のもくじはこちら：