書記が数学やるだけ#758 格子におけるミンコフスキーの定理

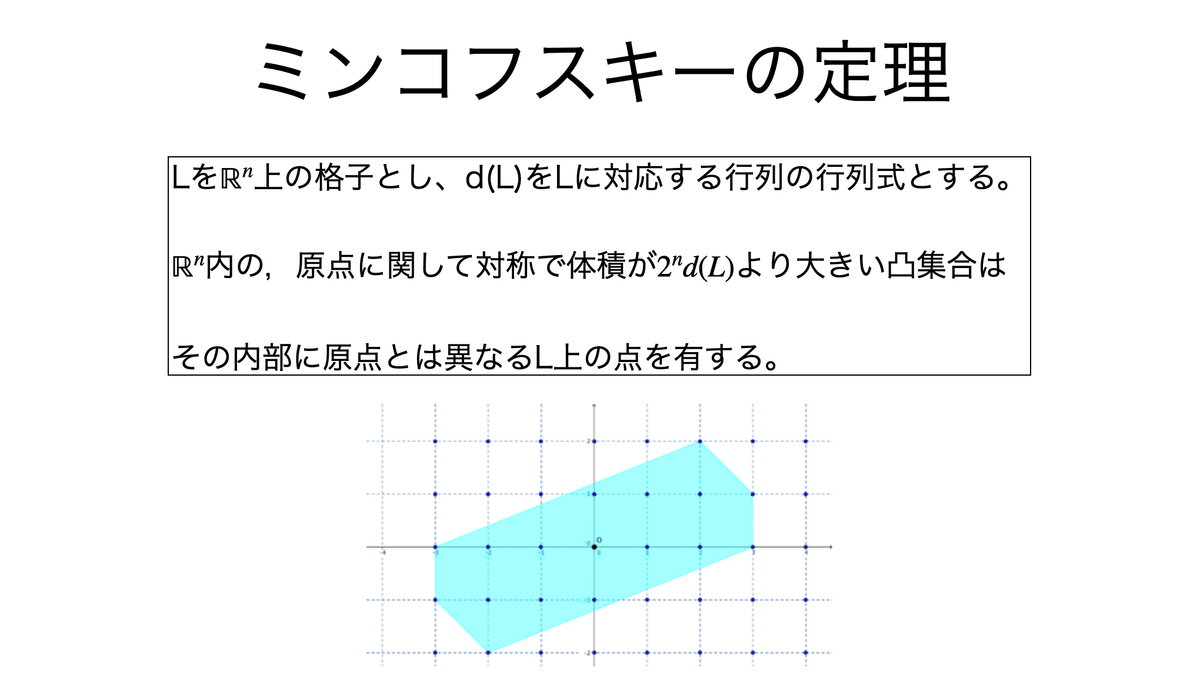
ミンコフスキーの定理は凸体と格子点の関係に関する研究を押し広げた。

問題

格子点にまつわる入試問題は発想力勝負といったところか。

説明

ミンコフスキーの定理は凸体の中の格子点の存在に関する定理で，原点に関して対称な凸集合は体積が十分大きいとき，必ず原点以外の格子点を有することを主張している。

解答

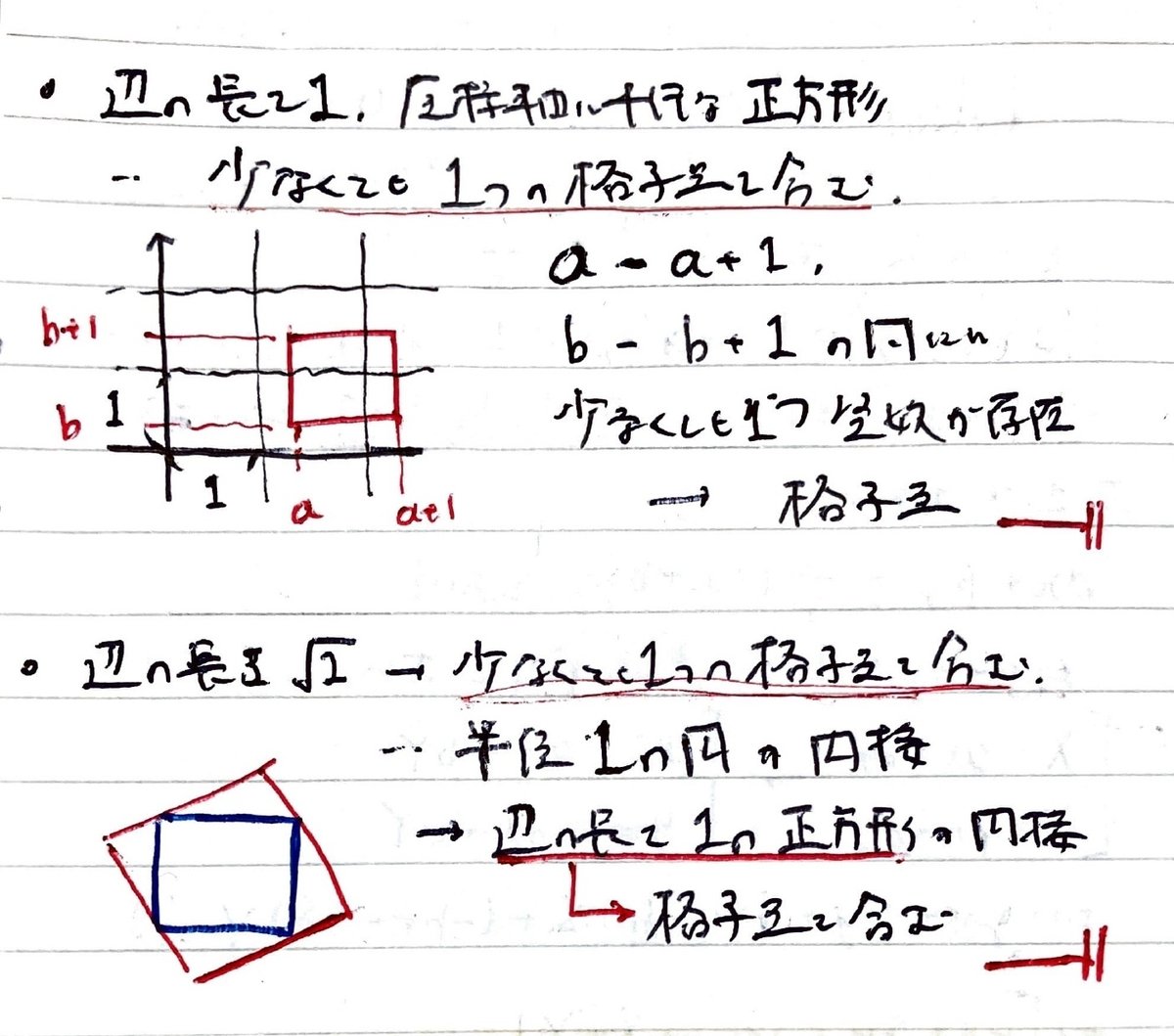
本問はミンコフスキーの定理の簡単な例で，格子点を頂点とした平行四辺形について示していく。

特に面積4の格子平行四辺形には内部または周上に中心以外の格子点が存在する。

まずは京大の問題，(1)は当たり前すぎてどこまで記述すべきか？(2)は(1)を利用することで簡単に示せるが，その場で思いついくかの勝負だっただろう。

次に東大の問題について。まずは格子点を数えやすいように1点を決めておく。ここで辺を傾きの曲線と示すことで個数を考えることができる。(2)は具体例を計算するだけ。ちなみに1992年東大数学理系は大問4の空間図形と展開図がかなりの難問であった。

本記事のもくじはこちら：