書記が数学やるだけ#811 楕円積分を用いた図形の周長

楕円関数を知ることで扱える数学の範囲が広がることを期待し，まずは楕円積分のモチベーションから見ていく。

問題

弧長は微分と積分両方を扱えるので入試問題ではちょうどいいと思われる。しかし，多くの図形の弧長は初等関数で表すことはできない。

説明

以下の定積分をそれぞれ，第一種・第二種・第三種の楕円積分という（標準形は変数変換の違い）。その名は「楕円の弧長」で出てくることに由来する。

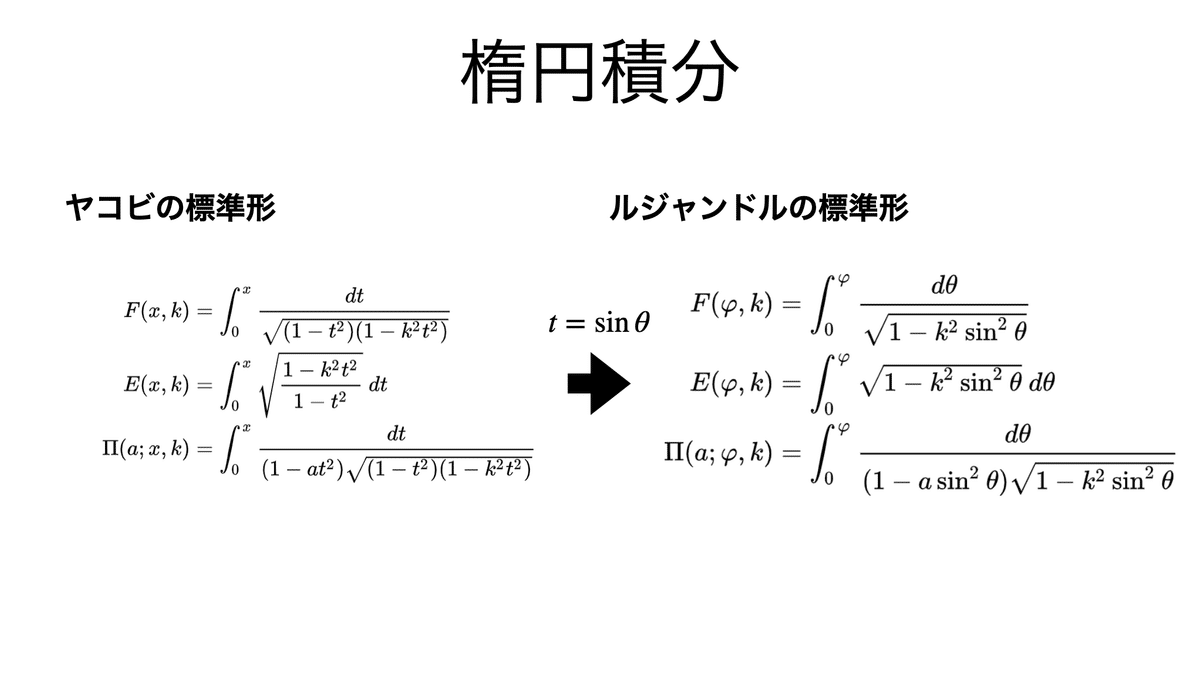
楕円の弧長では第2種楕円積分，レムニスケートの弧長では第1種楕円積分による表示が知られている。

レムニスケートについては以下を参照，このときは弧長の表示にβ関数を用いた：

レムニスケート周率は，直径に対する周長の比である。

解答

放物線の弧長を求める際に√x^2+a^2型の積分は登場する，いろいろ方法はあるが双曲線関数を用いるのがスマートだろう。似たような積分について：

楕円の周長を初等関数で表すことはできず，第2種楕円積分が必要になる。

レムニスケートでは第1種楕円積分が登場する。

レムニスケートの長さを直接求めることはできないが，問題で示した不等式から評価することは可能である。ここで広義積分であることに注意。

本記事のもくじはこちら：