書記が数学やるだけ#16 ニュートン法による近似，最適化のアルゴリズム（2021/01/17追記）

微分積分の応用として重要な最適化問題について，代表的なアルゴリズムであるニュートン法について紹介する。

問題

本問では，ニュートン法における3乗根の近似値の評価について扱っている。

公式

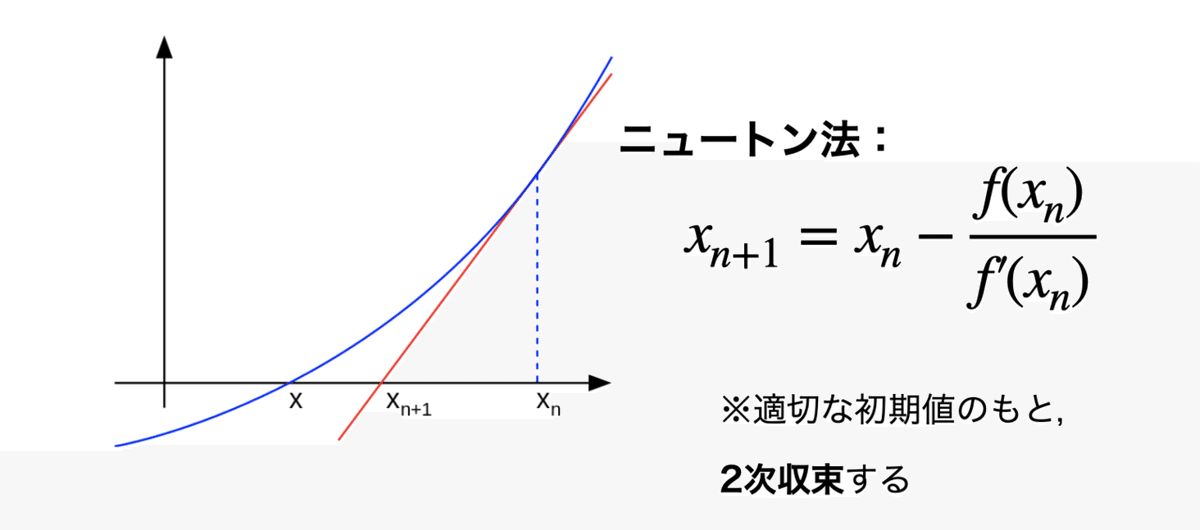
一般に多次元関数についても，行列を定義することにより計算できる。2次収束と収束が速いのが利点，欠点としてヤコビ行列の逆行列を求める必要があることをあげておく。改善策として，ヤコビ行列を必要としない準ニュートン法や，逆行列を求めることを避けられる共役勾配法などがある。

※2021/01/17追記

解法

とにかく面倒な計算が続く。(1)は数列が単調減少であることを示しており，徐々に実際の値に近づくことがわかる。

ここでは，ニュートン法が2次収束することを示す。

第5項における誤差を評価する。漸化式を繰り返し適用して解く。

Pythonによる実装

実際にコードを書いて検証してみる。関数としてルートの近似値を求める想定。

def root(k, c, x0 ,sigma):
    # 関数定義
    f = lambda x: x**k - c
    df = lambda x: k*x**(k-1)
  
  
    # リストのリセット
    rootlist = [x0]
  
    # ニュートン法で解を計算
    while True:
        x = x0 - f(x0) / df(x0)
        if abs(x-x0) < sigma:
            break
        else:
            x0 = x
            rootlist.append(x0)
  
    return x, rootlist

ルート2の近似：

#2の2乗根
a = root(2, 2, 1.5, 10**(-6))

print(a)

結果→(1.4142135623730951, 

[1.5, 1.4166666666666667, 1.4142156862745099, 1.4142135623746899])

問題(3)を検証してみる（プログラムそのものに生じる誤差は考えないことにする）：

#問題(3)
a = root(3, 2, 1.3, (2**(-5)) * (10**(-16)))

print(a)

結果→(1.2599210498948732, 

[1.3, 1.2611439842209073, 1.259922235393885, 1.2599210498959887, 1.2599210498948732])

第5項で計算がストップしており，ここで誤差が右辺以下になったことが確認できる。

本記事のもくじはこちら：