書記が数学やるだけ#809 物理におけるグリーン関数の例

ここまでの知識を用いて，物理におけるグリーン関数の例を挙げていく。

問題

説明

ここでは簡単な例としてポアソン方程式を解説する。これは楕円型偏微分方程式に分類される：

解としてグリーン関数を含む積分を仮定し，代入することでデルタ関数を含む微分方程式を得る。

これをフーリエ変換して係数比較することで，グリーン関数を求めることができる。

静電ポテンシャルは，ポアソン方程式の解の定数倍で得られる：

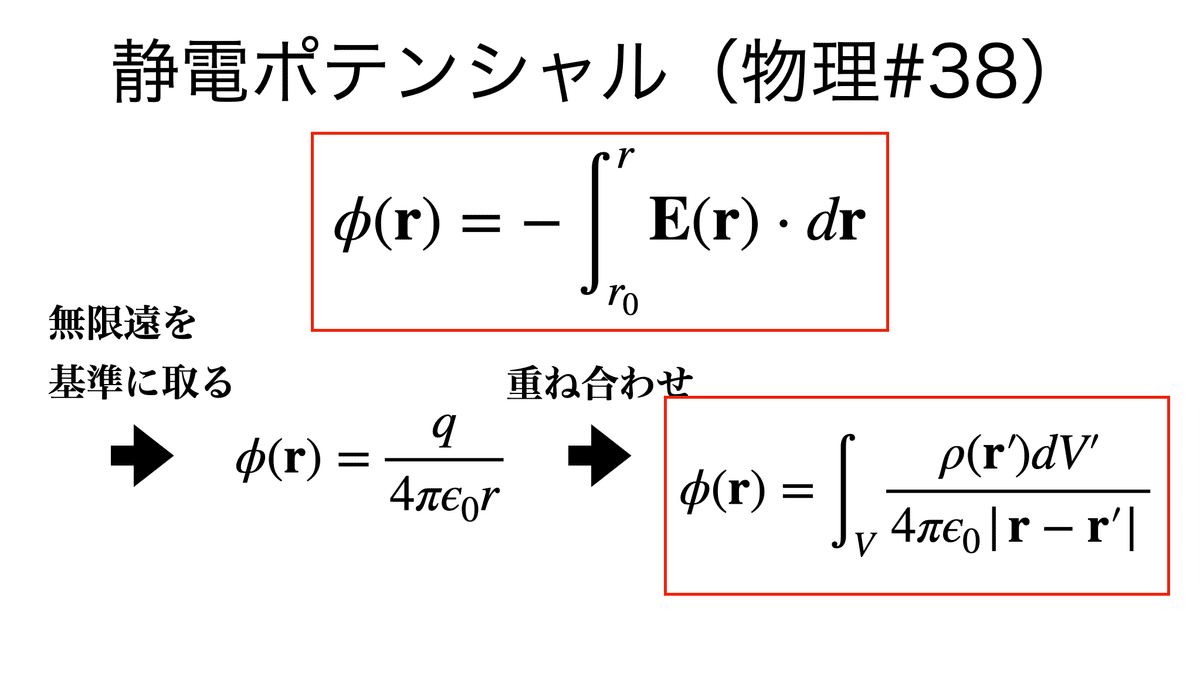
以前はデルタ関数の性質から導出したが，やっていることは本質的には同じである：

次に拡散方程式について，これは放物型偏微分方程式に分類される：

波動方程式は双曲型偏微分方程式に分類され，様々な分野に応用される：

最後に一つまだ物理で扱っていないが，相対論的量子力学で出てくるクライン-ゴルドン方程式について，ここまで来ればグリーン関数を求めるのは難しくない。

解答

拡散方程式では，位置xと時間tの2変数についてグリーン関数を考える。

あとは前回までの知識で導出できる。ここで，解の形が正規分布であることに注目。

波動方程式はヘルムホルツ方程式に変換することができ，得られた微分方程式は前回までとやることは同じなので以後省略する。

静電ポテンシャルからは，極の選び方により遅延グリーン関数・先進グリーン関数の2つが得られる。

クライン-ゴルドン方程式は，相対性理論と量子力学の組み合わせから導出され，これはヘルムホルツ方程式に帰着できる。なお，ここで得られた解は湯川ポテンシャルに対応している。

本記事のもくじはこちら：