書記が数学やるだけ#66 最小二乗法の基本
「最小二乗法」という単語は,最近の機械学習ブーム(?)で知っている人も多いだろう。今回はその方法の基本事項についてザックリ解説する。
問題
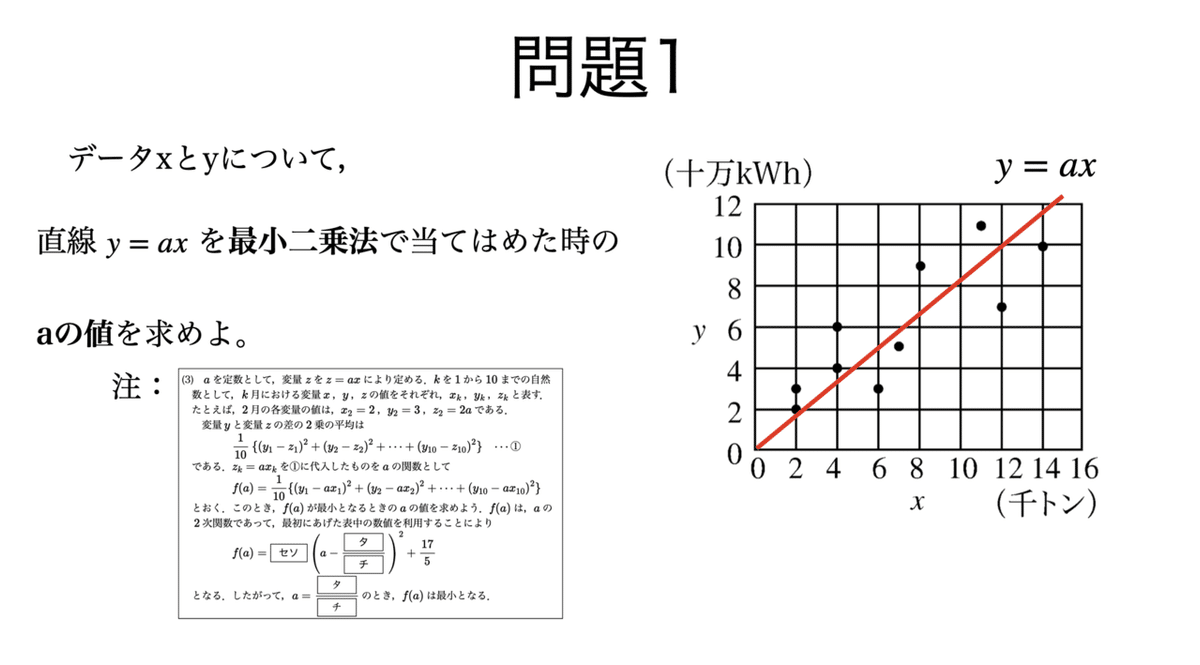
入試問題で最小二乗法に関連したものがないか調べたところ,センター試験追試にその前例があることを見つけた。丁寧な誘導で基本事項について問うものであったが,初見だと混乱したかもしれない。

ついでに,正規方程式に関連した問題も。

説明
最小二乗法について,例えば単回帰問題だとその傾きと切片で尤もらしい値を推定する問題に帰着する。
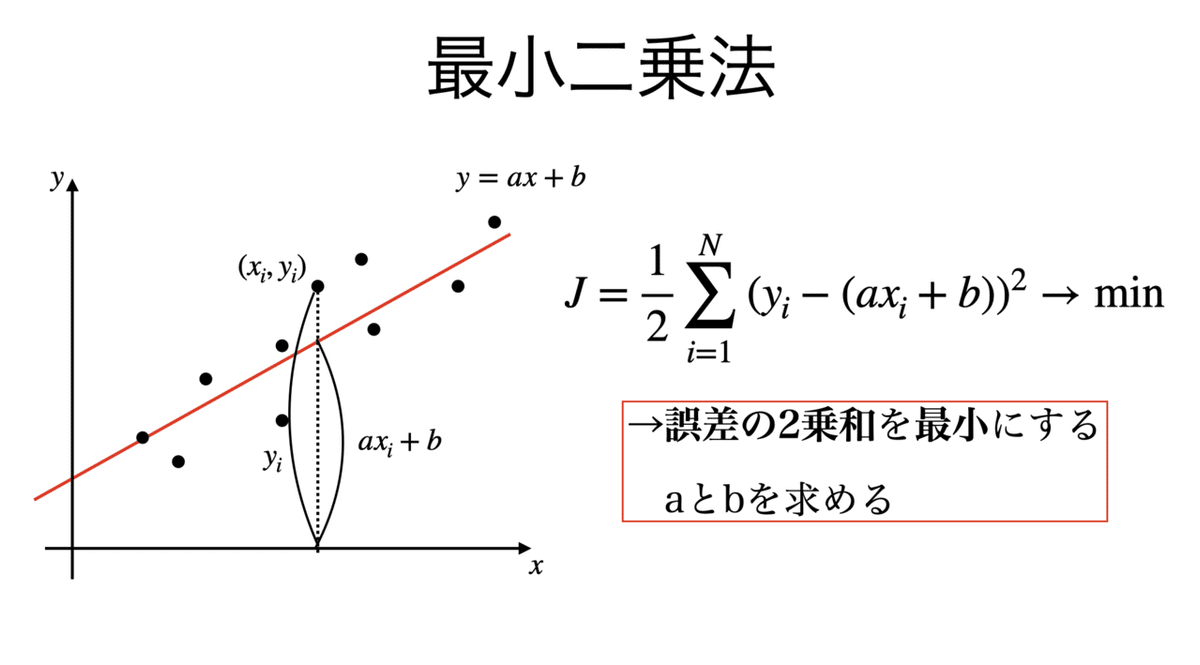
誤差を最小化したいのはわかる,ではなぜ2乗するのか?それは単純に計算しやすいからである。また,1/2をかけているのも計算をしやすくするためにつけたものに過ぎない。
これをベクトルと行列で表現するとスマートである。

最小化が「微分した式=0」に対応するので,それに基づいてできた方程式(正規方程式)を解く。

連立方程式が解けるのなら,それが最適解になる(Ax=bをxについて解けばいい)。
しかし,方程式と未知数の数が一致するとは限らない,そうなると基本的に解を求めることはできない。そんな場合でも,最小二乗法では,なるべくよく合う解を求めることができる。

方程式が少ない場合は,ラグランジュの未定乗数法に対応する。


まとめると,正規方程式の解は以下のようになる。なお,一般逆行列を定義することで統一することができる。

解法
あらかじめ誘導として与えられている式に従うことにする。

展開して同類項をまとめると,あらかじめ問題に表示されている数字に置き換えられる。あとは誘導通り平方完成して,最小値が求められる。

院試の問題から引っ張ってきたが,正規方程式を覚えるか導出するかしたらすぐに解けるものだった。

式に代入してxを求める。

なお,(1)は単純に連立方程式を解くだけでも求められる。
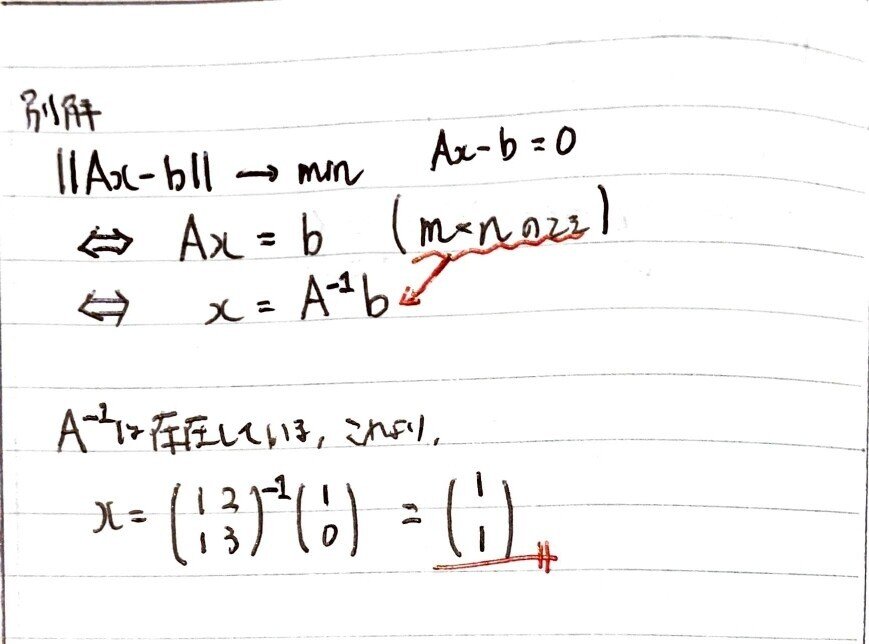
(2)以降は,Aについて逆行列が定義できない。しかし一般逆行列なら定義できるので,それを用いる。

本記事のもくじはこちら:

