書記が数学やるだけ#686 双対空間

テンソル代数を考える準備として，双対空間を導入していく。

問題

説明

双対空間V*とは，V上の線型写像φ:V→F（すなわち線型汎函数）全体の成す集合であり，それ自身がF上のベクトル空間となる。双対空間の元のことを余ベクトル，共変ベクトル，一次形式などとよぶ。

2つのベクトル空間と双線形形式からなる3つ組を双対対という。

双対空間においても基底を考えることができる（双対基底）。

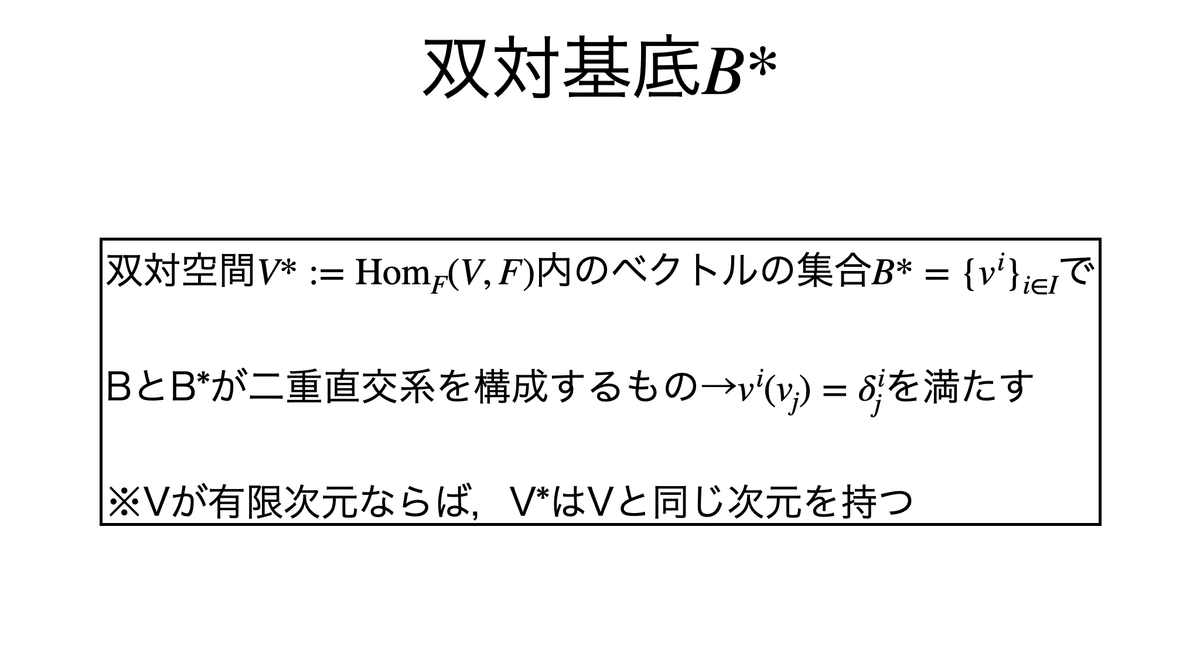
解答

双対基底について，線形独立と線形和を示す。

双対の双対は元の空間と線形同型である。この同型は基底の選び方によらないものであり，カノニカルであるといえる。

基底変換について，表現行列が転置となる点に注目。

本記事のもくじはこちら：