書記が経済やるだけ#34 期待効用仮説，ポートフォリオ選択

不確実性を評価する方法について，入門を見ておく。

問題

期待効用という考え方を導入する。

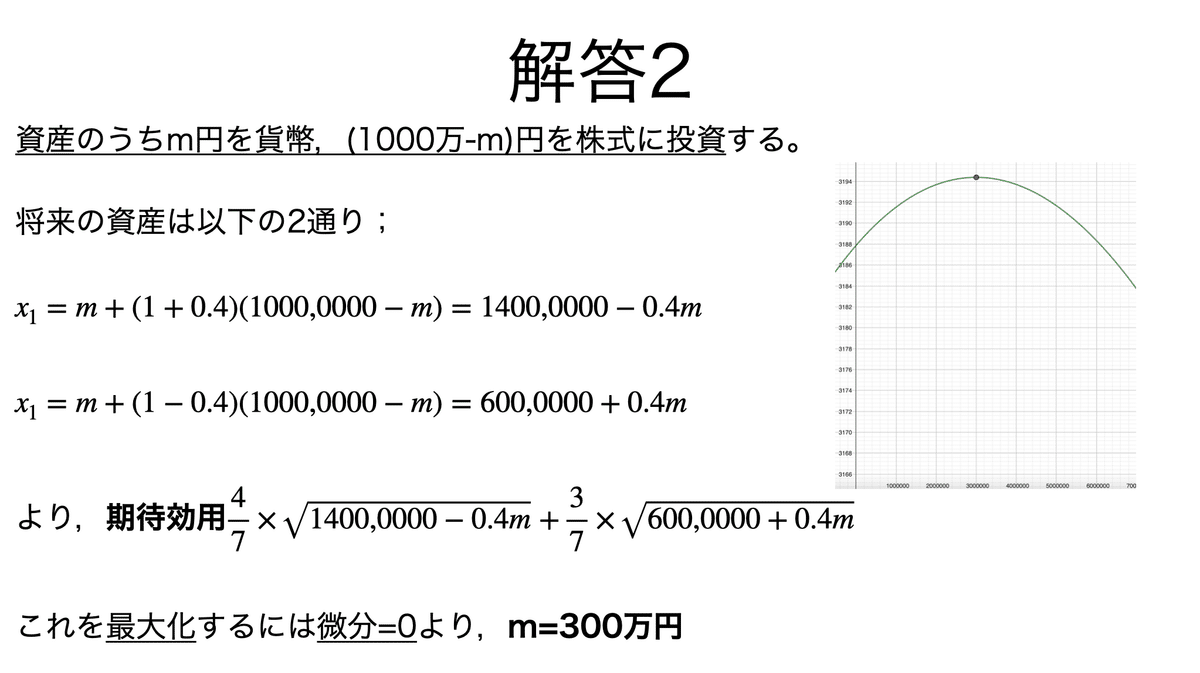
もう一問，ポートフォリオの初歩的な計算を行う。

説明

サンクトペテルブルクのパラドックスは，1738年，サンクトペテルブルクに住んでいたダニエル・ベルヌーイにより，学術雑誌『ペテルブルク帝国アカデミー論集』の論文「リスクの測定に関する新しい理論」で発表された。ここでは期待値が現実には必ずしも適用できないことを示し，代わりに「期待効用」を導入した。

期待効用仮説では，不確実性下にある個人は，期待効用最大化公準に基づいて（この期待効用を極大化するように）行動すると仮定する。中でも，ジョン・フォン・ノイマンとオスカー・モルゲンシュテルンの名前をとってフォン＝ノイマン・モルゲンシュテルン効用関数が重要である。

リスクに対し，危険回避的な個人の期待効用関数は対数や平方根など，危険愛好的な個人の期待効用関数は指数などで表される。

解答

期待値・期待効用は定義通り計算する。ここでくじ引きよりも定額をもらう方を選ぶ金額について解くと，119円以上なら定額を選ぶということで，くじ引きの期待値199円よりも低いことから，この個人は危険回避的である。

ポートフォリオの簡単な例として，安全資産（貨幣）と危険資産（株式）の2つを考える。期待効用を最大化することで，安全資産と危険資産の両方へのリスク分散が示される。

本記事のもくじはこちら：