
書記が数学やるだけ#60 線形計画の基本定理
今回から,3回にわたって線形計画問題について扱う。
参考書:
まず,線形計画問題がどのような形をしているかから見ていく。
問題
問題自体は,高校数学の領域の問題である。
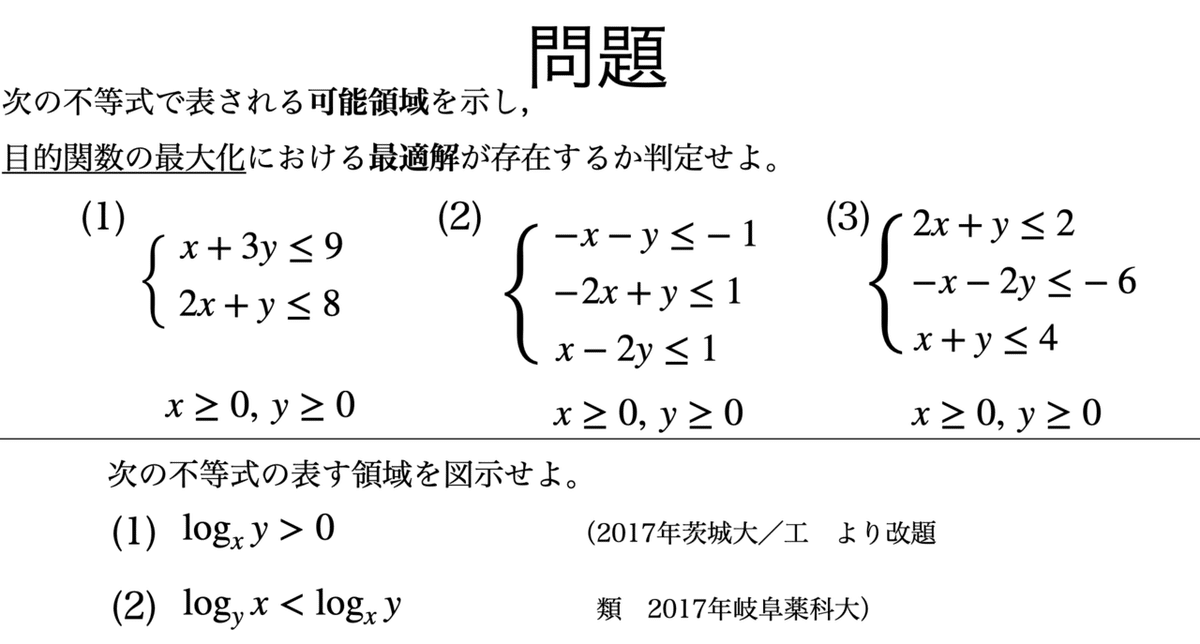
説明
線形計画問題は,制約条件と変数,目的関数からなり,制約条件と目的関数が1次式である。


線形計画の基本定理は重要で,これより解の候補が絞り込める(高校数学の問題はこれを暗黙の了解としている場合がほとんど)。

スラック変数を導入することで,制約式を等式に置き換えられる。あとは,スラック変数を含めて目的関数を最大化するような変数を求めればよい,ということになる。

解法
不等式の共通範囲を図示する。可能領域が図のように閉じていれば,最適解が存在することがいえる,

以下の2つは,最適解が存在しないケースである。


さて問題を変えて,こちらは主に対数の基本を問うものである。
とにかく真数と底の条件を忘れずに。右辺を同じ底の対数で示して,底により場合分けして,図示する。

底を揃えて,不等式を満たすような値を場合分けしつつ求めていく。

最終的に図示したものがこちら。経験しておかないと手が詰まりかねないので,一度は解いておきたい問題である。

本記事のもくじはこちら:
リニューアル

