書記が数学やるだけ#854 単体の向き，境界準同型

トポロジーについて，まずはホモロジー論から進めていく。

問題

説明

ホモロジー（homology）は与えられた数学的対象，例えば位相空間や群に，アーベル群や加群の列を対応させる一つの一般的な手続きをいう。

単体は，点・線分・三角形・四面体・五胞体といった基本的な図形の n 次元への一般化である：

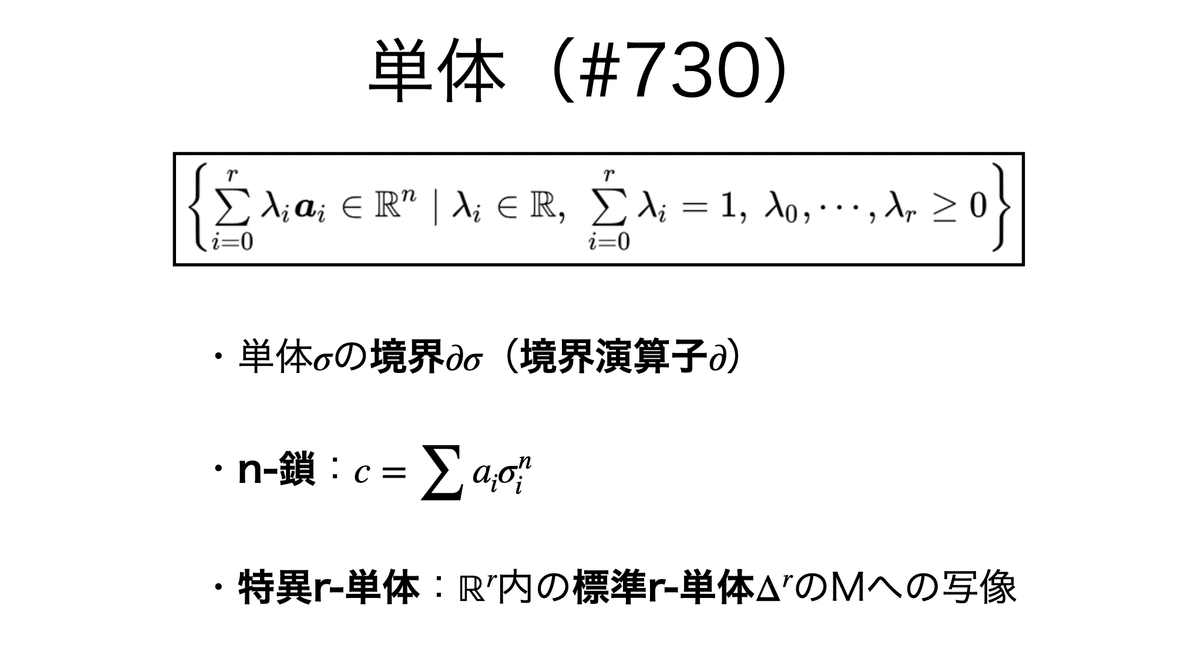
複体は単体分割することができる。

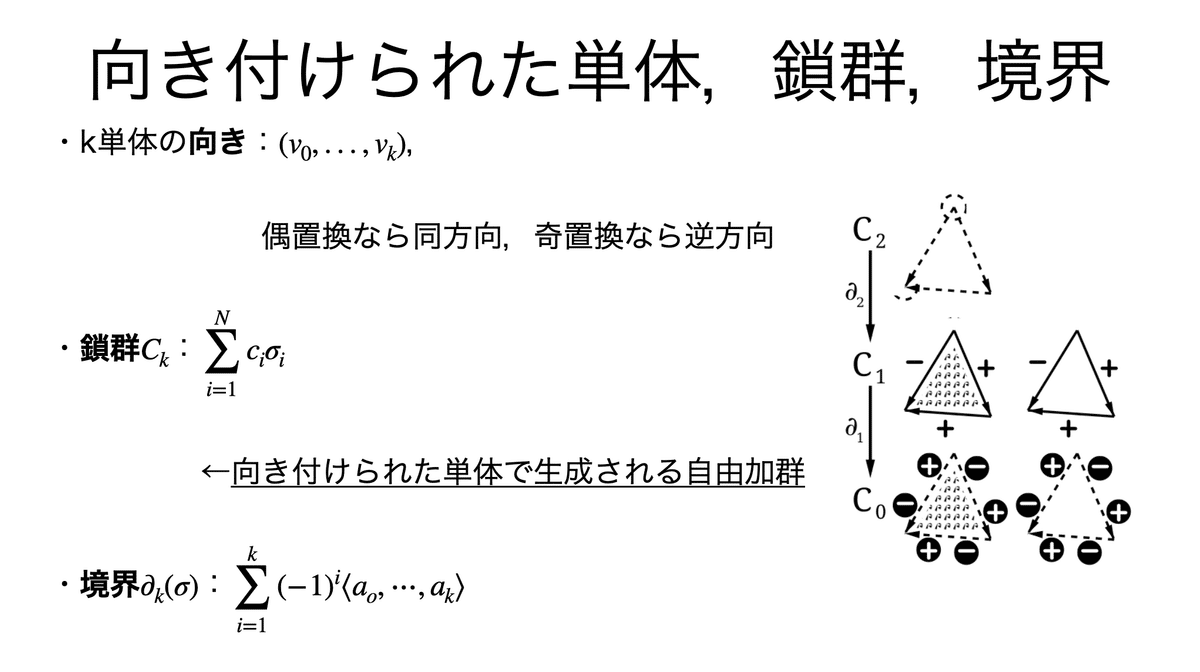
ここで，単体に向き・鎖・境界といった概念を導入する。

解答

鎖について，点と辺の例を示しておく。

k=1の境界準同型について，線形性と準同型から辺から点に変換することができる。

次の例は境界準同型が0になるパターンで，ちょうど図形を1周した場合に相当する。

輪体群は境界準同型の核で定義される。具体的な計算には行列を用いると便利である。

2次元図形の境界準同型について。2つ目の式は境界の境界はないことを示している。

本記事のもくじはこちら：