
書記が物理やるだけ#339 結晶系の分類
固体物理学・物性物理学について,まずは結晶について概観する。
問題
②は大学入試の数学から,ミラー指数に関連する内容を計算しておく。

説明
結晶は並進対称性を有するものと定義され,単位格子を3次元的に繰り返し並べたものとして記述される。

3次元の最密充填構造には六方最密充填と面心立方格子があり,充填率は約74%である。このことは1611年ヨハネス・ケプラーにより予想された(ケプラー予想)が,これが解決したのは2014年と400年以上後のことであった。

ミラー指数は結晶の格子中における結晶面や方向を記述するための指数で,英国の鉱物学者ウィリアム・ハロウズ・ミラーによって考案された。

解答
まず単純立方格子,体心立方格子,面心立方格子の基本並進ベクトルを示しておく。
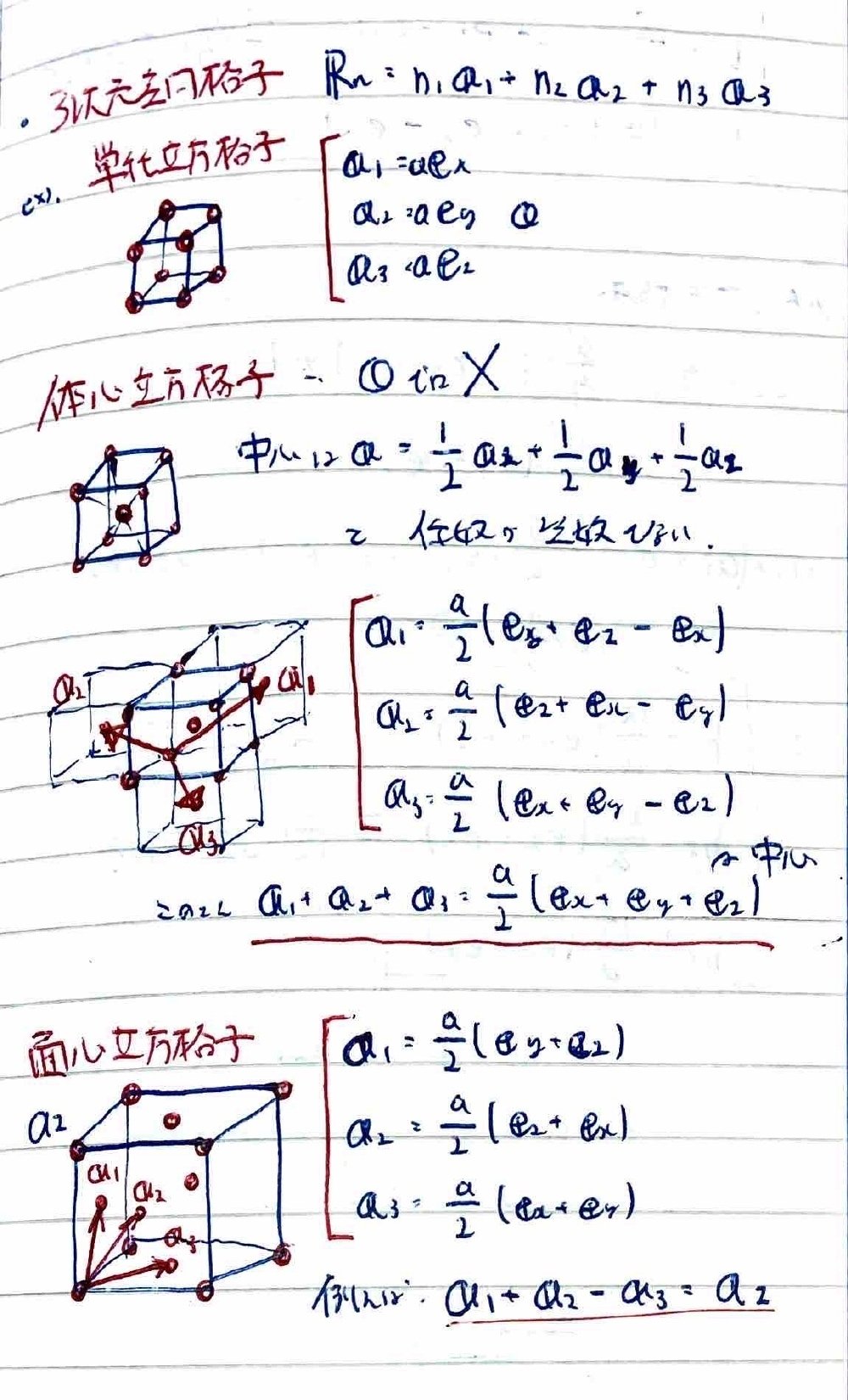
充填率を計算するには,最近接原子間距離と単位胞の体積を用いる。

六方最密充填についての計算では,空間認識の能力が問われる。

ミラー指数(hkl)の決定には各軸の切片の逆数を計算する必要がある。
本問の(1)において,dは隣接する(hkl)面の間隔に相当する。(2)はコーシー-シュワルツの不等式が使える形である。

(3)では条件をもとに文字数を減らし,微分により極大値を求める。

本記事のもくじはこちら:

