
書記が数学やるだけ#832 空間から平面への射影
射影幾何学への入門として,平面幾何を空間に落とし込んで考える方法を見ていく。
問題

説明
デザルグの定理は射影幾何学における基本的な定理の一つである。ユークリッド幾何では平行線や無限遠について例外的に扱う必要があるが,射影幾何学では同様に扱うことができる:

3円から生じる共点について,モンジュの定理が成り立つ。

解答
空間におけるデザルクの定理は,以下のような位置関係で表される。

次元が上がると難しくなるかと思いきや,空間同士の交線より容易に示せてしまう。

平面の場合で示すには,平面上の点の空間に持ち上げることで空間版デザルクの定理に帰着させる。逆にいうと,空間から平面への射影をとることで空間版と同じことを平面でも示せる,ということになる。

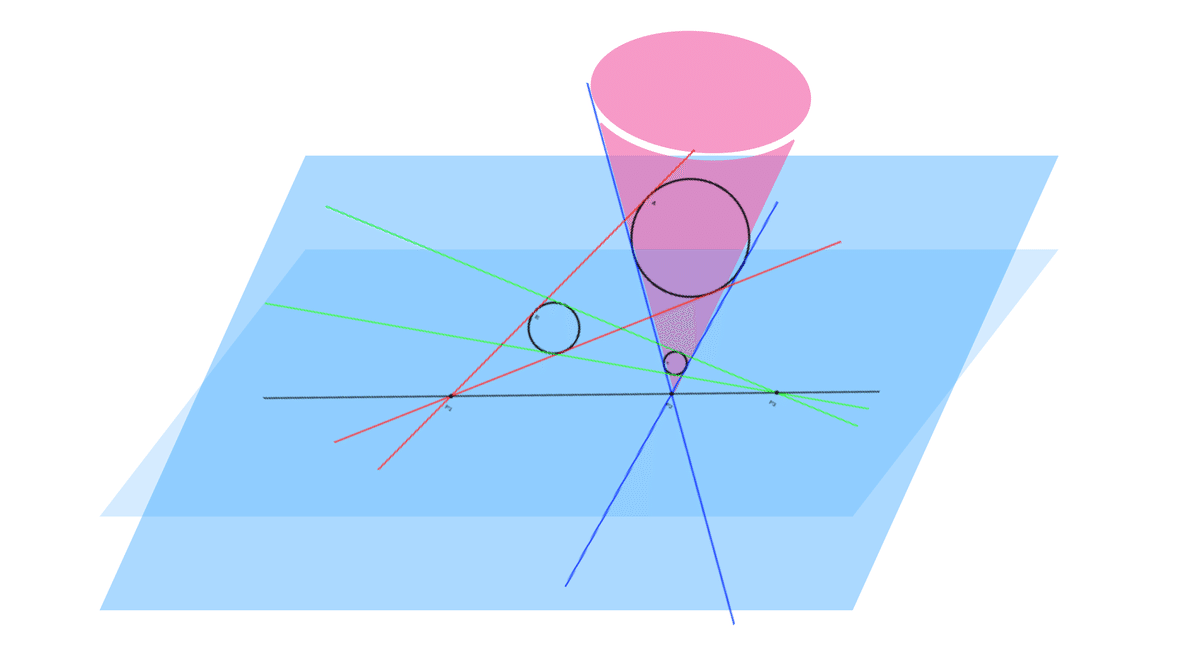
もう一つの例であるモンジュの定理では,円を球に見立てて上から平面で覆い,2つの球を覆う円錐の頂点を求めることで,底面と上平面の交線から共点であることが示せる。

本記事のもくじはこちら:
学習に必要な本を買います。一覧→ https://www.amazon.co.jp/hz/wishlist/ls/1XI8RCAQIKR94?ref_=wl_share
