
書記が数学やるだけ#679 ディリクレ問題-1
楕円型偏微分方程式についていくつか性質を見ていく。
問題

説明
楕円型偏微分方程式の代表例がポアソン方程式である。

物理的な応用は多い,まずは万有引力ポテンシャル:

静電ポテンシャルについて:
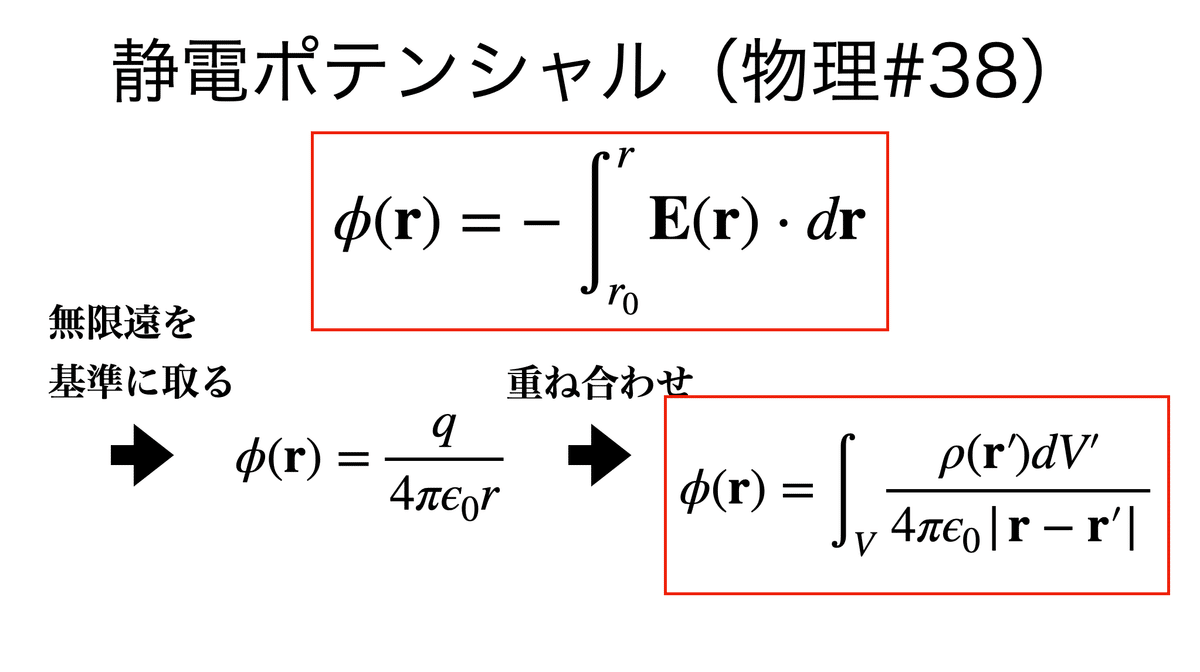
特に境界値の取り方で区分される。

解答
円環領域におけるディリクレ問題を解いてみる。

境界条件より,各係数は以下の連立方程式の解である。

いくつか具体例を示す。

三角関数の直交性などを駆使して計算量を減らしていく。

最後に一つ,外部問題はケルビン変換により内部変換い置き換えることができる。

本記事のもくじはこちら:

