
書記が数学やるだけ#714 テンソル積の構成
テンソル積について,抽象と具体の双方から見ていく。
問題

説明
テンソル積の定義を以下に示す。
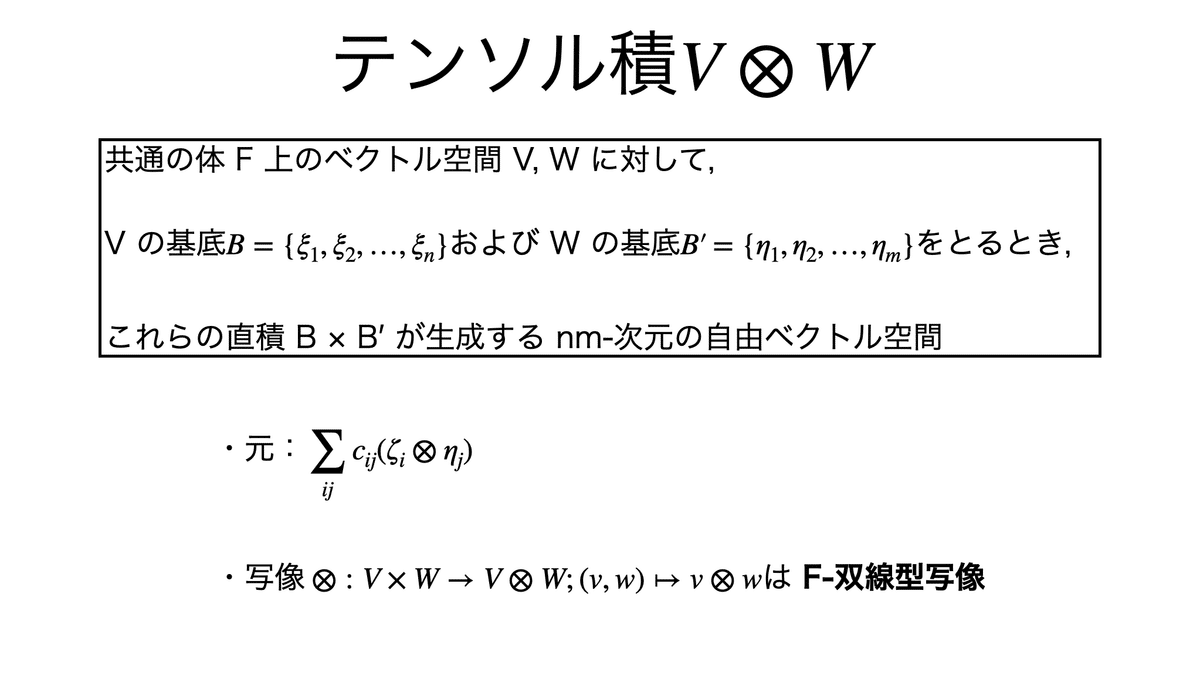
テンソル積は普遍性を満たす。

特殊例として,線型写像のテンソル積は行列で表される。

解答
テンソル積における普遍性を示す。この辺は代数学の準同型写像あたりを参考にするとよい。

ここで用意したΦ0は双線型写像であり,fは一意なので以下の合成写像を定めることができる。

もう一つ,カノニカルについて例を示しておく:

具体的な計算をいくつか。まず,テンソル積は可換でないことに注意。

双対基底を含んだ少し複雑な例だが,やることは単なる展開である。

本記事のもくじはこちら:

