書記が数学やるだけ#255 無限乗積

解析学の前半の締めとして，無限乗積について扱う。

問題

説明

無限乗積の収束について，対数で無限級数に変換できることを利用する。

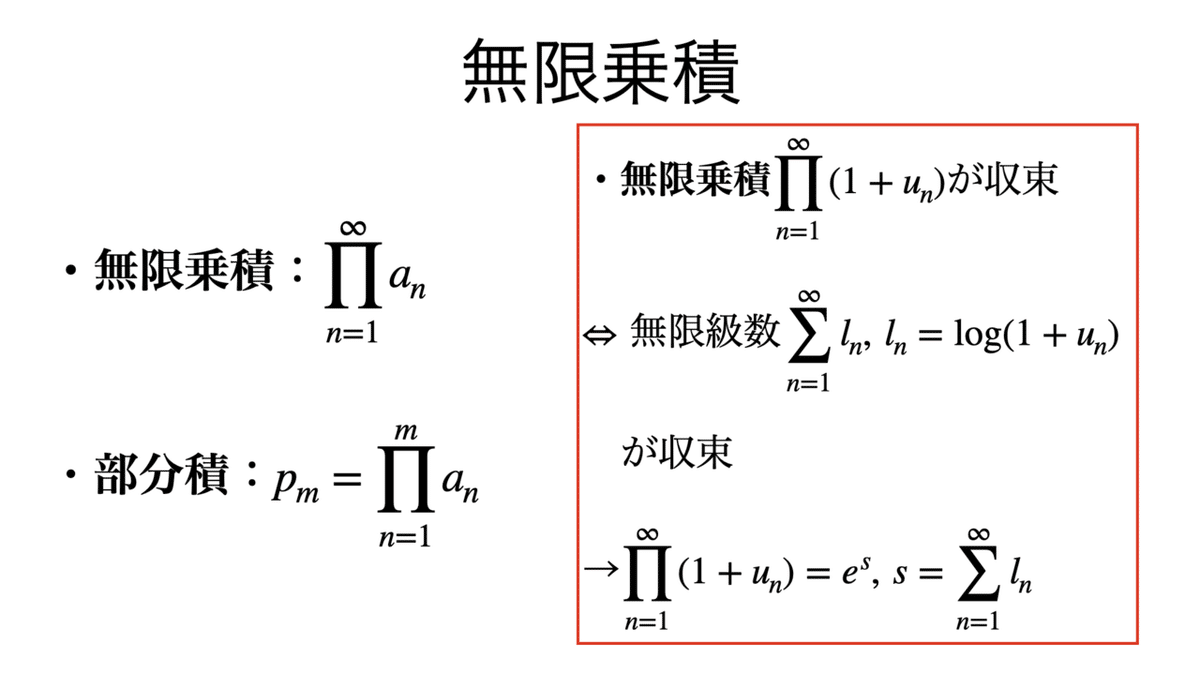
解答

まずは収束に関する定理を証明しておく。

Wallis積分からWallisの公式を示す。

ガンマ関数が収束することの証明。

優関数を用いて収束することを示す。

最後に，円周率を2だけで表示するVieteの公式を示す。これは過去いくつかの大学入試問題があるが，初見では厳しい計算が多い。その到達感は如何なるものだろうか。

本記事のもくじはこちら：