
書記が数学やるだけ#494 リウヴィルの定理,ゲルフォント=シュナイダーの定理
少しだけ超越数の話をする。
問題
横浜市大のこの問題は,かなり巧妙な発想を要する。

説明
多項式の解になる数を代数的数,ならない数を超越数という。

リウヴィルの定理は,代数的数であるための条件を与える。
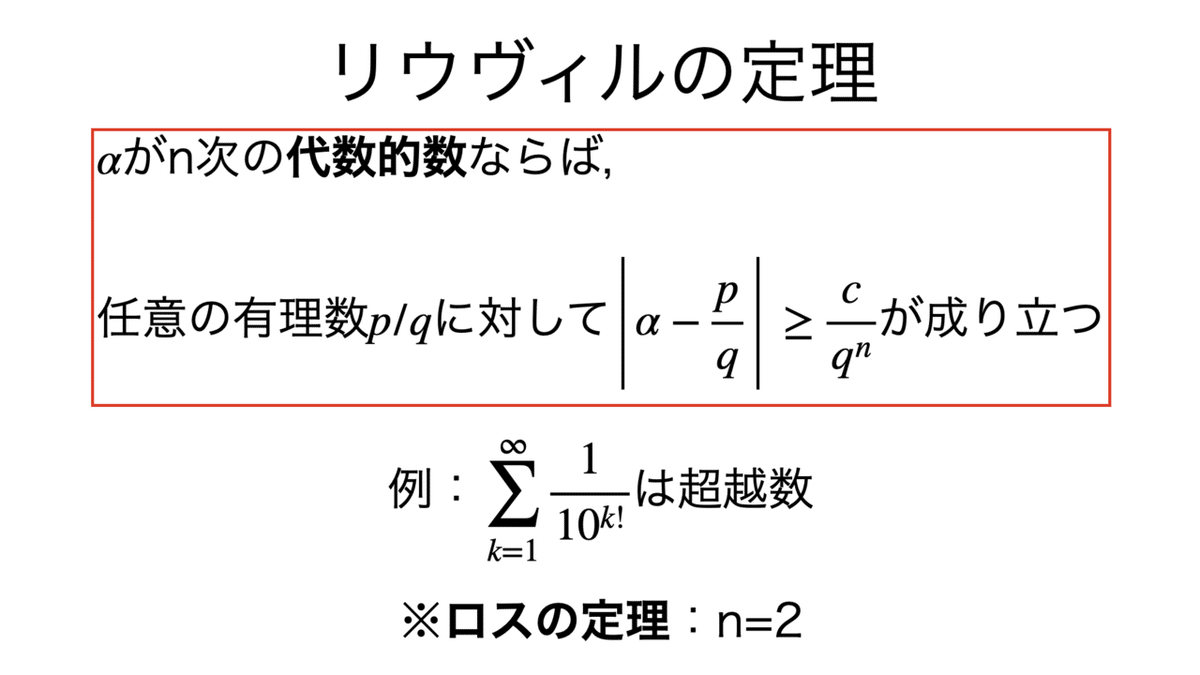
以下,超越数に関する定理をいくつか列挙する。


解答
リウヴィルの定理の証明は,不等式評価の連続である。



リウヴィルの定理が成り立たないことから,超越数であることが示せる。

こちらは大学入試の問題だが,「有理数か無理数かによらず存在性が示せる」のはなかなか難しが鮮やかな発想である。

本記事のもくじはこちら:

