
書記が数学やるだけ#860 道とホモトピーの演算
今回からホモトピーを扱うことにする。
問題

説明
ホモトピーという概念は,ざっくり言うと道やループから図形の穴を調べるものと言える。これは連続写像に一般化することができる。
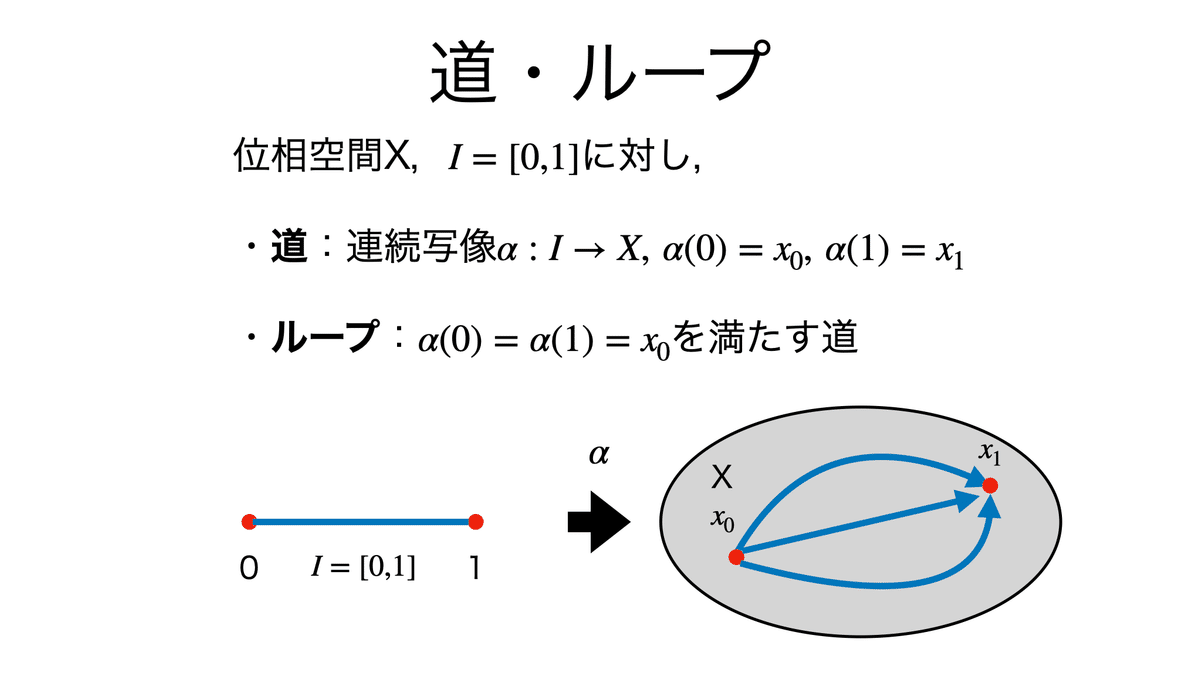
写像におけるホモトピー・ホモトピックの定義について。これは同値関係であることからホモトピー同値とも呼ばれるが,後に示す位相空間におけるホモトピー同値と区別するため,ここでは単にホモトピックと記載する。

基本群は,ループのホモトピー類の集合で定義される。

解答
ホモトピックは同値関係であることを示すために,反射律・対称律・推移律を確認する。反射律・対称律はほぼ当たり前だが,改めて数式で確認する。

推移律を示すには,新たにHという写像を用意する。

このHは,[0,1]×[0,1]の下半分をF,上半分をGで写す写像となっている。

道の積について,これは2つの道を連結する操作に該当する。

これは左半分と右半分ことの写像から示せる。

結合律は今回で一番手間がかかる。ここで左辺と右辺では道から道へと乗り換える際のsの値が異なり,変形のパラメータtによりsを連続的に変えるようにFを設定する。

αからβでの乗り換えについて,左辺は1/4,右辺は1/2で切り変わるようsを変化させる。またβからγでの乗り換えについて,左辺は1/2,右辺は3/4で切り変わるようsを変化させる。

単位元の存在について,道における単位元は点から動かないことに相当する。
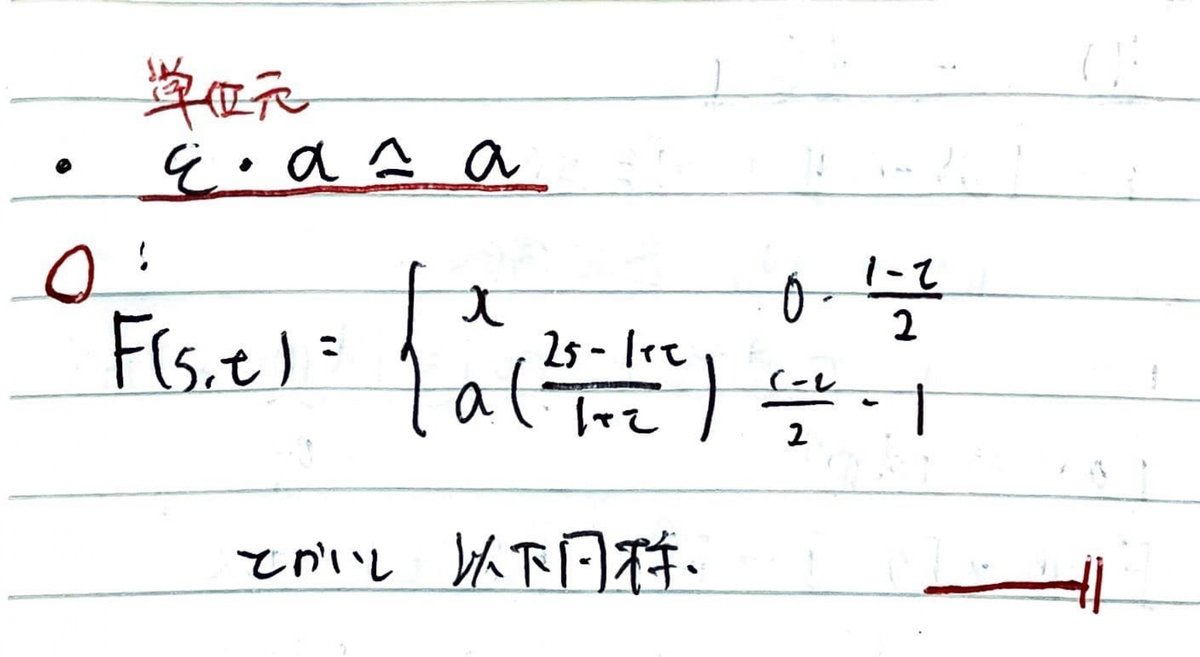
この場合,左辺は1/2,右辺は0で切り替わるように設定すれば良い。

逆元の存在についても同様。

左辺は行って同じところに帰る操作に該当する。

本記事のもくじはこちら:

