書記が数学やるだけ#857 グラフの同相とホモロジー群の同型

グラフの同相とホモロジー群の同型の関係について，具体例から見ていく。

問題

全ての場合の証明は手間がかかるので，1次ホモロジー群に限定して考える。

説明

「辺の反転，辺の細分とその逆，レトラクション」といった操作では，ホモロジー群は同型を保つ。これを用いてグラフを簡素化してホモロジー群を求めることができる。なお，逆は成立しないことは向き付けを扱う際に触れる。

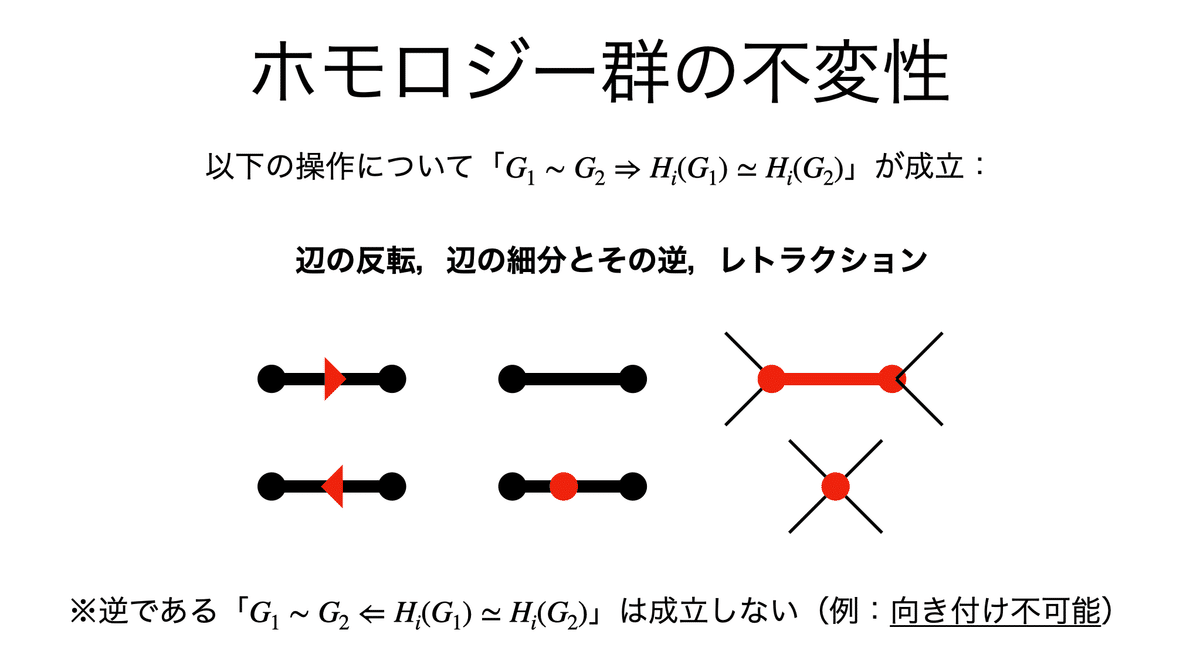
解答

1次ホモロジー群の辺の反転についてのみ詳細に見ていく。最終的には，グラフの辺における同型写像を示すこととなる。

写像とその核の含有関係については具体的な計算が必要。

準同型かつ逆写像から，同型が示せた。

辺の細分・レトラクションについては以下のように辺と写像を設定すれば，あとは同様にして計算するだけである。

アニュラスの単体分割について，辺の細分の逆を繰り返し用いることで2次元単体と同型であることが言える。

トーラスについて，2次ホモロジー群は容易に決まる。

1次ホモロジー群の導出には，辺の細分の逆により得られた外部と内部を用いる。

本記事のもくじはこちら：