
【日常数学】データに騙されるな①
1.はじめに
平均とは何か、本当に理解できていますか?当たり前じゃん、と思う方が多いと思います。しかし、実は大学生の4人に1人が理解できていないという調査結果があります。

こちらの問題に取り組んでみてください。

日本数学会の大学生数学基本調査からの出題です。

正解は、(1)✕、(2)〇、(3)✕ です。

この調査は、全国の国公私立48大学の1年生を中心とした5934人を対象にし、3問すべて正解した学生は、76.0%でした。
(1)を〇だと思った人は、平均=真ん中と勘違いしているのだと思います。データの真ん中の値は中央値です。
(3)を〇だと思った人は、平均=最も多いと勘違いしているのだと思います。データの最も多い値は最頻値です。
多くの人が平均値の計算はできると思います。しかし、平均の本当の意味は理解できていない人がいるのです。そして、本当の意味がわかっていないと、データに騙されてしまうことがあるのです。
2.平均の意味
では、平均の意味とは何でしょうか?それは、「平らに均すといくつになるか」ということです。だから、真ん中の値とも最も多い値とも限りません。
次の例を見てみましょう。

会社A、Bの給料を比べると、Aのほうが全体的に高そうですよね。しかし、実際に平均値を計算してみると、両者同じなのですね。これは、会社Bにとんでもなく給料の高い社員がいるからです。このように、他と比較して極端に大きい(もしくは小さい)値を外れ値といいます。外れ値がある場合、平均値が外れ値に引っ張られてしまいます。そのため、データを見るときに平均値をそのまま鵜呑みにしてしまうのは危険です。
では、何を基準に考えればいいのでしょうか。全体の真ん中を基準にすればいいですよね。すなわち、中央値です。
では、両者の中央値を見てみましょう。
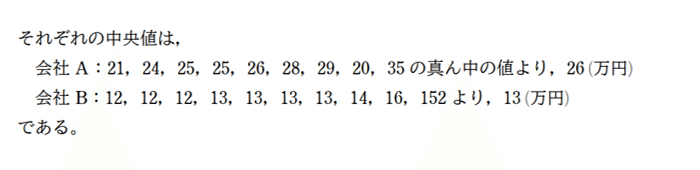
外れ値を含む会社Bについては、平均値の27万円とは全く異なりますよね。だから、平均=真ん中の値とは限りません。外れ値を含む場合は、中央値を参考にするといいでしょう。
また、平均=最も多い値とは限りません。
両者の最頻値を見てみましょう。

外れ値を含む会社Bについては、平均値の27万円とは全く異なりますよね。
では、実際のデータを見てみましょう。

これは、総務省統計局の貯蓄現在高階級別世帯分布です。2人以上の世帯の貯蓄額の平均値は1791万円です。結構、みんな貯金があるな、と感じるかもしれません。ですが、そうではなく、一部のお金持ち(貯蓄額4000万円以上)によって平均値が引き上げられているのです。中央値を見てみると1061万円です。
平均の意味を理解し、データに騙されないようにしたいですね。
3.おわりに
平均は真ん中とは限らない、最も多いとも限らない、とわかっていただけたと思います。しかし、それらが一致することもあります。それは、データが正規分布をなす場合です。例えば、身長や体重、など平均値にデータが多く集まり、それ以下と以上が左右対称になる、日常生活にありふれたデータです。
例えば、靴のサイズを見てみましょう。

平均値と中央値、最頻値が大体同じですよね。
以下は、正規分布の場合とそうでない場合の平均値、中央値、最頻値です。

平均の意味を真ん中や最も多いと勘違いしてしまうのは、正規分布が日常にありふれているからかもしれません。
しかし、きちんと意味を理解し、データに騙されないようにしましょう。
