
数学オリンピック(JMO)予選2024の解説①
マロ&ミケ:あけましておめでとうございます!
ミケ:いやの間にかクリスマスとか正月とかイベントごとが終わってたね!
マロ:だねー。でも何か忘れてない?
ミケ:お年玉のこと?ちゃんと飼い主さんから美味しいお年玉もらったけど?
マロ:そうじゃなくて、数学オリンピック!!1/8に今年の予選があったじゃん!!
ミケ:あぁ~!確かに!
マロ:まったく、忘れっぽくて困るなー。
ミケ:ごめんごめん。じゃあ今日は数学オリンピックの解説だね!
マロ:そうだね!最初の三問はミケでも解けたんだっけ?
ミケ:うん!最初だけだけどね(笑)
マロ:じゃあミケがその三問で残りで解説できるやつを僕がしようかな。
ミケ:おお~!
ミケ:じゃあ新年一発目ということではりきっていきましょー!
マロ:おー!!
次回↓
数学オリンピック(JMO)の解説②|マロとミケのブログ (note.com)
数オリの問題のURL
問題のURLはこちらです。
https://www.imojp.org/archive/mo2024/problems/jmo34yq.pdf
数オリ解説(1~3まで)
受けた感想/全体の印象(ミケ)
じゃあここからはミケが解説していくね。
まず問題を解いてみた感想だけど、
…あれ?今年、なんかむずくね?
って思った!
一応二週間前くらいから大体10年分の過去問(2012~2023)を解いてたんだけど、2018あたりから急に簡単になってたから今年も簡単だろうなって思ってたんだよね。
あと、単純に点が取れるようになってきて若干天狗になってたのもあるだろうけどね。
だから最初に問題全体を一瞥した時、直感で今年はやばいって悟った!
実際解いてみると、1~3は点取り問題で全然簡単だったんだけど、4からとたんに解けなくなった。
1~3全部で30分で解き終わったから、残り時間をほぼ全部使って4,5,6,7を考えてみたんだけど、ひとっつも解けなかった!
5とかは正直見たことない組み合わせ(ガウス記号とCombination)だったから、やっぱり数オリの壁は厚い!!って感じたよ。
第一問の解説
問題はこんな感じだったね。
以下の数は有理数である。これを既約分数の形で表せ。
$${\displaystyle\sqrt{\frac{123!-122!}{122!-121!}}}$$
最初にこれを見たとき、オワッタ…って思ったね(笑)
でもよくよく考えてみれば、意外と簡単なんだよね。とりあえず、ルートの中身に注目しよう。
$${\displaystyle \frac{123!-122!}{122!-121!}=\frac{122!(123-1)}{121!(122-1)}=\frac{122\times122}{121}=\frac{122^2}{11^2}}$$
よって二乗の形ができたわけだから、答えは$${\frac{122}{11}}$$になるね。
組み合わせとか順列の計算で階乗に慣れていたら一瞬でできる問題だね。ちょっとメタ考察すれば、こういうタイプの問題はちょっとした工夫だけで簡単な計算に落とし込めるんだよね。大体1番の問題だしね。間違っても愚直に分子と分母を計算しちゃだめだよね。
第二問の解説
どの桁に現れる数字も素数であるような正の整数を素敵な数とよぶ。3桁の正の整数nであって、n+2024とn-34がともに素敵な数である者はちょうど2つある。このようなnを全て求めよ。
ミケは最初この問題を見たとき飛ばすことを決意したよ。繰り上がりとか考えるのが面倒だし、なにより「○○な数」タイプの問題は頭を使う問題が多いからね。(結果ほかの問題も解けなくてこの問題に戻ってきてしまったんだけども。)
どの桁も「素数」っていう条件はかなり強力だから、簡単に絞り込めそうだね。とりあえず求めたい$${n}$$を次のように置こうか。
$${n=100a_3+10a_2+a_1\quad(a_1,a_2,a_3\in\{0,1,2,\dots,8,9\})}$$
この時各桁の値$${a_3,a_2,a_1}$$は素数でもなんでもないことに注意しなきゃね。素敵な数なのはあくまで$${n+2024,n-34}$$の二つだからね。
とりあえず、$${n+2024\cdots[1]}$$と$${n-34\cdots[2]}$$を計算してみようか。
$${[1]n+2024=(2)1000 +(a_3)100+(a_2+2)10+(a_1+4)}$$
$${[2]n-34=(a_3)100+(a_2-3)10+(a_1-4)}$$
この時、各桁が素数になっていればいいってわけだね。素数である一桁の数は$${2,3,5,7}$$ってことも頭の片隅に置いておこう。
とりあえず地道に一の位から考えてみようか。繰り上がり、繰り下がりに注意したら
$${[1]a_1+4 =5,7,12,13\leftrightarrow a_1=1,3,8,9 }$$
$${[2]a_1-4=-3,2,3,5\leftrightarrow a_1=1,6,7,9}$$
問題によれば、nは[1],[2]のどちらでも素敵な数にならないといけないわけだから、$${a_1=\dots}$$の共通の数字だけ取ればいいね。つまり、$${a_1=1\hspace{1mm}or\hspace{1mm} 9}$$だと絞れたね!!
これでマロがいつも口酸っぱく言ってる「範囲を絞る」ができたね。
しかも考えてみたら、[1][2]を満たすnは「ちょうど二つ」あるわけで、(これはミケが答えがわかってたから言えたことで、別に一桁目が1で二桁目三桁目の候補が複数出る場合もある。早とちりはいけないね(笑))
範囲を絞った結果二つの候補が現れたわけだから、この二つの候補(1と9)がどちらも求める答えになるんだね!!
…まぁ本当はこれが本当に答えなのかを最後に確かめなければいけないんだけど、数オリだからそういうのは無視しちゃおう。
それじゃあ一桁目が1のときと9のときで場合分けしてnを求めていこう。
一桁目が1のとき
この時、[1]の二桁目は$${(a_2+2)}$$で、[2]の二桁目は繰り下がりがあるわけだから$${(a_2-3 -1)=(a_2-4)}$$になるね。
じゃあこの状態でどちらも素数となる数字を求めると、
$${[1]a_2+2=2,3,5,7\leftrightarrow a_2=0,1,3,5}$$
$${[2]a_2-4=-3,2,3,5\leftrightarrow a_2=1,6,7,9}$$
よって共通しているのは$${a_2=1}$$
最後に三桁目を求めていこう。[2]に繰り下がりがあるのを忘れないようにね!!
$${[1]a_3=2,3,5,7}$$
$${[2]a_3-1=2,3,5,7\leftrightarrow a_3=3,4,6,8}$$
共通しているのは$${a_3=3}$$
したがって一つ目のnは$${n=311}$$一桁目が9のとき
この時、[1]の二桁目は繰り上げに注意して$${(a_2+2+1)=(a_2+3)}$$で、[2]の二桁目はそのまま$${(a_2-3)}$$だね。
このとき、どちらも素数となる数字を求めると
$${[1]a_2+3=3,5,7,12\leftrightarrow a_2=0,2,4,9}$$
$${[2]a_2-3=-3,2,3,5\leftrightarrow a_2=0,5,6,8}$$
よって共通する数字は$${a_2=0}$$
最後に三桁目を求めよう。[2]のときに繰り下がりがあることに気を付けよう。
$${[1]a_3=2,3,5,7}$$
$${[2]a_3-1=2,3,5,7\leftrightarrow a_3=3,4,6,8}$$
共通しているのは$${a_3=3}$$
したがって二つ目のnは$${n=309}$$
これで二つのnが求まったので、答えは$${n=309,311}$$だね!
繰り上がりと繰り下がりも考えないといけないから頭がこんがらがっちゃうよね。こういうときは各桁の数字が高々$${a=0\backsim 9}$$しかないことから全部代入しちゃうのがいいかもね。実際僕も全部代入したし(笑)
ちょっと時間をかければ解けるからここはみんな取れそうだね。
第三問の解説
次がミケができる最後の問題だね。
一辺の長さが10の正三角形ABCがある。Aを通る円が変BC(端点を除く)と点Xで接し、辺AB,ACとそれぞれAでない点D,Eで交わっている。BX>CX,AD+AE=13がともに成り立つとき、線分BXの長さを求めよ。ただし、PQで線分PQの長さを表すものとする。

この問題と図を見たミケの第一印象は、「方べきのにおいがする!!」と「BX>CXってことは二次方程式かな?」だよ。
とりあえず、問題からわかることを図に書き込んでみようか。
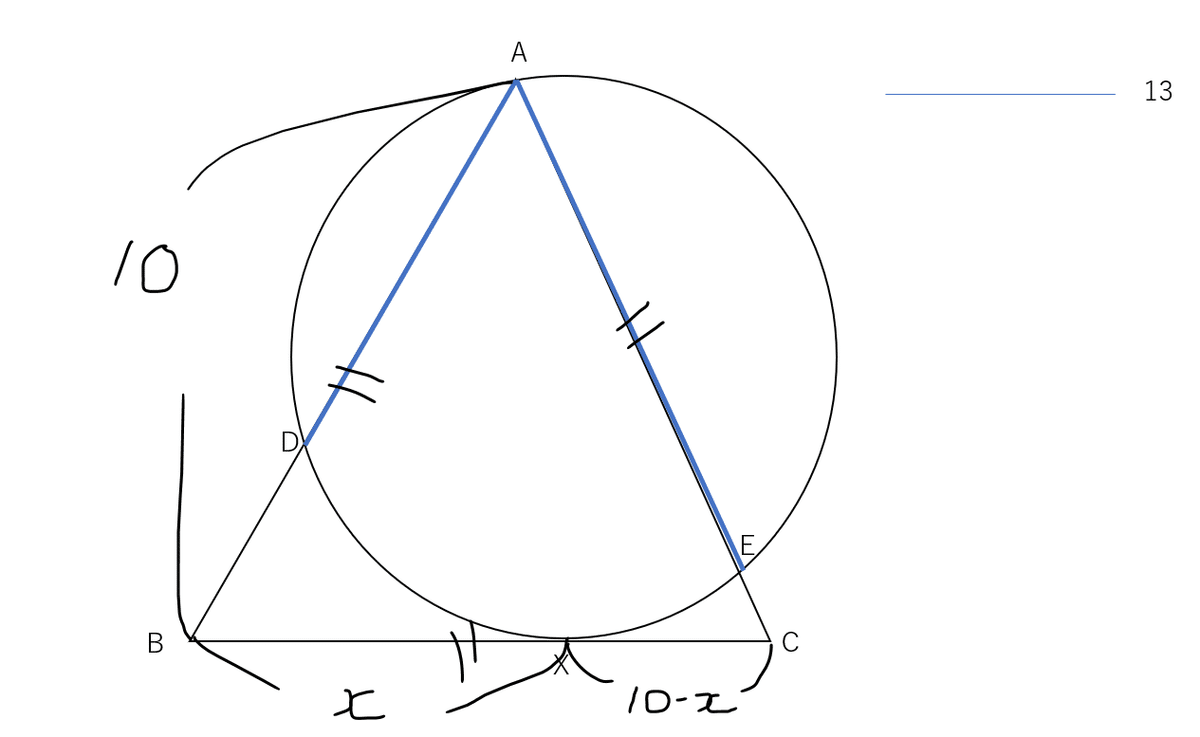
求めたいところを$${x}$$で置いているよ。
じゃあ方べきの定理を使っていこう。まずは下図のように方べきの定理を適用すると

$${BD\times10=x^2}$$
となるね。あとから条件$${AD+AE=13}$$を使えるようにするために$${BD=10-AD}$$を代入しておけば、
$${10(10-AD)=x^2\leftrightarrow 10AD=100-x^2\cdots(1)}$$
図を見ると方べきの定理がもう一回適用できそうだよね。同じように下図のように方べきの定理を適用してあげると

$${CE\times10=(10-x)^2}$$
あとは条件$${AD+AE=13}$$を使えるようにするために$${CE=10-AE}$$を代入しておけば、
$${(10-AE)\times10=(10-x)^2\leftrightarrow 10AE=100-(10-x)^2\cdots(2)}$$
よって(1)+(2)より、
$${10AD+10AE=100-x^2+100-(10-x)^2\leftrightarrow130=-2x^2+20x+100}$$
あとはこの二次方程式を解くだけだね!式変形して
$${-2x^2+20x-30=0\leftrightarrow x^2-10x+15=0}$$
二次方程式の解の公式より
$${\displaystyle x=\frac{10\pm\sqrt{100-60}}{2}=\frac{10\pm2\sqrt{10}}{2}=5\pm\sqrt{10}}$$
となるね。あとはプラスを取るかマイナスを取るか…だけど。
条件によるとBX>CXなんだよね。とりあえず、CXを求めてみようか。
$${CX=10-BX=10-x=10-(5\pm\sqrt{10})=5\mp\sqrt{10}}$$
なるほど。BXとCXは$${\pm}$$が違うだけなんだね。ってことは明らかにプラスを取るときが大きいんだから$${BX=5+\sqrt{10}}$$だね!
この問題は方べきの定理さえ知っていればすぐ解けたね。円と接線で長さを求めるときたら方べきの定理がまず候補に挙がるよね。
条件が難しそうだけど、とりあえず手を動かせばわかりそうな問題だね。
終わりに
ミケ:ふぅう~。久しぶりで疲れた~~。
マロ:お疲れ様!今年はどうだった?
ミケ:うーん、まぁ難しかったよ。
ミケ:でも最初の三問は解けたからよかった!
マロ:おおー。ミケの目標の三問が達成できたもんね。
ミケ:うん!でもほかの問題は全然わかんなかったからマロに教えてほしい!
マロ:任せてー! わかりやすく説明できるよう頑張ります!
ミケ:ありがとう!!来週が楽しみだな~。
誤字脱字、質問等あったら遠慮なくどうぞ!!
ーミケー
