
結び目理論を簡単に②
今日は飼い主が出かけています。しかし飼い主はずぼらなのでいつもキッチンの小窓の鍵は開いています。今日はそこからミケに入ってもらいました。
「たまにここから入れてくれるけど防犯のためにも飼い主さんに占めてもらったほうがいいんじゃない」
「でもそんなことしたらミケが来れなくなっちゃうじゃん。マロも外に出られなくなるし…。誰か通れるほどの窓じゃないから猫専用の扉ってことにしておこうよ」
「まあマロがそう言うならいいのかな? ところで、今日も呼んだってことは結び目理論の話の続きかな?」
「そうだよ。ミケは察しがいいねぇ」
「確かこの前話しきれなかったジョーンズ多項式の話だよね。楽しみ!」
今回は前回の「結び目理論を簡単に①」の続きです。こちらをご覧になってから今回の「結び目理論を簡単に②」を読んでいただけると一層楽しめると思います。
前回の復習
前回は主に交点数ごとの結び目について紹介と、結び目の見分け方としてアレクサンダー多項式を用いて見分ける方法を紹介しました。
そして最後に、結び目には右手型と左手型に分けられる結び目がある子を紹介しました。例としては三葉結び目です。また、8の字結び目は右手型と左手型が一致する両手型結び目でした。
アレクサンダー多項式は結び目の種類は見分けられたものの、その結び目が右手型なのか左手型なのか、または両手型結び目なのかが判定できませんでした。
そこで今回はジョーンズ多項式を紹介します。
結び目と絡み目
ジョーンズ多項式の前に、絡み目を説明します。
絡み目とは、結び目が何本も絡まったもののことを言います。結び目自身は、結び目が一本だけ絡まった絡み目とも言えます。
以下に有名な絡み目であるポップ絡み目、ホワイトヘッド絡み目、ボロミアン環を紹介します。
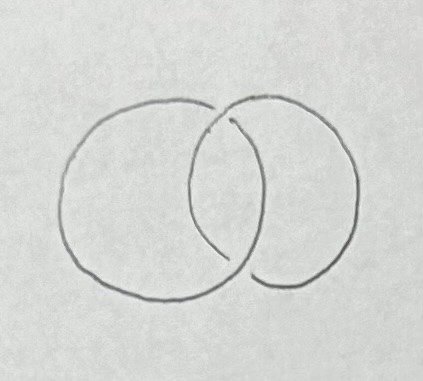

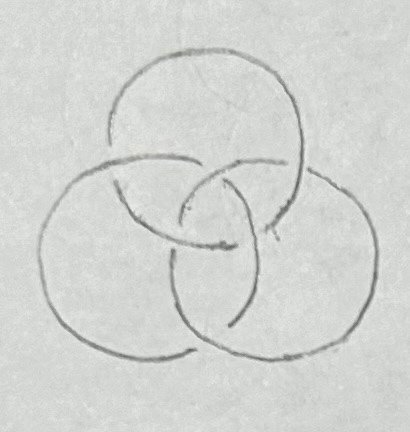
n本の結び目が絡まった絡み目をn成分の絡み目と言います。ポップ絡み目とホワイトヘッド絡み目は2成分の絡み目、ボロミアン環は3成分の絡み目です。
また、2つの自明な結び目が三次元空間上に、ある平面を隔てて存在している絡み目を自明な絡み目と言います。結び目同士が交わっていなくても絡み目と言えるんですね。

あと1つ、言葉を定義します。結び目や絡み目は三次元空間上に存在しますが、このブログ内、また紙面では二次元で表現されています。これを結び目や絡み目の射影図と言います。
ジョーンズ多項式
まず、ジョーンズ多項式は「ある結び目とその鏡像が一致するかどうか」が判定できます。
まずはアレクサンダー多項式同様、結び目の向きを決めます。
結び目または絡み目$${L}$$のジョーンズ多項式を$${V_L(t)}$$と表します。$${V_L(t)}$$は次の2つの式を繰り返し適用することで求めることができます。
自明な結び目を〇とすると、$${V_〇(t)=1}$$
$${t^{-1}V_{L_+}(t)-tV_{L_-(t)}=(t^{\frac{1}{2}}-t^{-\frac{1}{2}})V_{L_0}(t)}$$
ここでの$${L_+}$$、$${L_-}$$、$${L_0}$$は、それぞれ$${L}$$の1つの交点を+交点、-交点、スムージング(今回は0交点と言うようにします)で置き換えてできるもののことを指します。
また、この2つ目の関係式はスケイン関係式と言います。

そして、ジョーンズ多項式を実際に計算する際はスケイン木を描きます。スケイン木の描き方は次の通りです。
結び目の1つの交点に注目する。このとき、この交点は+交点、-交点、0交点のどれかである。
その交点を、他の2種類に置き換えてできた絡み目を描く。
これが自明な結び目になるまで繰り返す。
こうしてできたスケイン木を自明な絡み目から逆にたどっていくことで、このスケイン木の起点にある結び目のジョーンズ多項式が求まります。
では、実際に三葉結び目と8の字結び目のジョーンズ多項式を求めてみましょう。
計算例
三葉結び目
まずは右手型の三葉結び目から求めてみましょう。次のように向きを決めます。
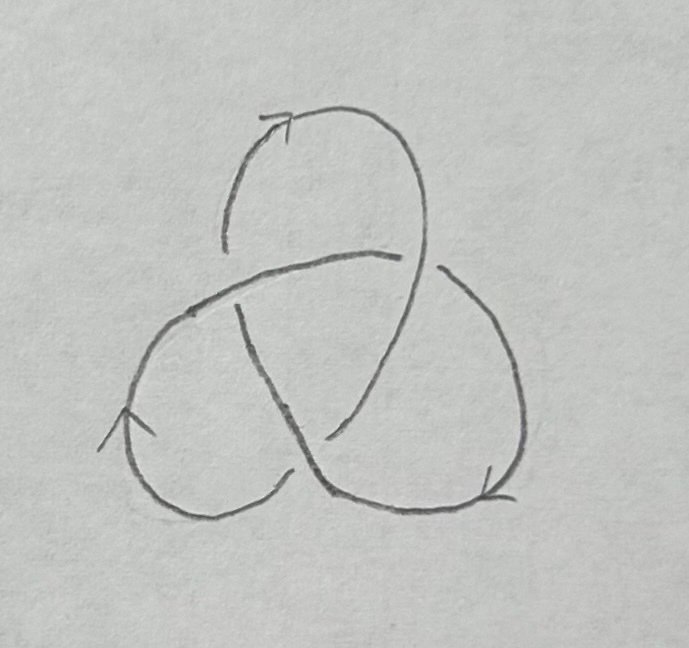
そして先ほど紹介した手順に則ってスケイン木を描いていきます。

では、①の時のジョーンズ多項式をスケイン関係式から求めてみましょう。
すると、ジョーンズ多項式$${V_{L_{1,0}}(t)}$$は次のようになります。
$$
\begin{array}{lcl}
V_{L_{1,0}}(t) & = & \displaystyle\frac{t^{-1}V_{L_{1,+}}(t)-tV_{L_{1,-}}(t)}{t^{\frac{1}{2}}-t^{-\frac{1}{2}}}\\\
& = &\displaystyle\frac{t^{-1}\cdot1-t\cdot1}{t^{\frac{1}{2}}-t^{-\frac{1}{2}}}\\\
&= & -t^{\frac{1}{2}}-t^{-\frac{1}{2}}\\\
\end{array}
$$
次に、②の時のジョーンズ多項式$${V_{L_{2,+}}}$$を求めましょう。次のようになります。
また、$${V_{L_{2,-}}=V_{L_{1,0}}}$$です。
$$
\begin{array}{lcl}
V_{L_{2,+}}(t) & = & t\lbrace tV_{L_{2,-}}(t)+(t^{\frac{1}{2}}-t^{-\frac{1}{2}})V_{L_{2,0}}(t)\rbrace\\\
& = & t\lbrace t(-t^{\frac{1}{2}}-t^{-\frac{1}{2}})+(t^{\frac{1}{2}}-t^{-\frac{1}
{2}})\cdot1\rbrace\\\
& = & t(-t^{\frac{3}{2}}-t^{\frac{1}{2}})\\\
& = & -t^{\frac{5}{2}}-t^{\frac{1}{2}}
\end{array}
$$
最後に③の時のジョーンズ多項式$${V_{L_{3,+}}}$$を求めましょう。次のようになります。
また、$${V_{L_{3,0}}=V_{L_{2,+}}}$$です。
$$
\begin{array}{lcl}
V_{L_{3,+}}(t) & = & t\lbrace tV_{L_{3,-}}(t)+(t^{\frac{1}{2}}-t^{-\frac{1}{2}})V_{L_{3,0}}(t)\rbrace\\\
& = & t\lbrace t\cdot1+(t^{\frac{1}{2}}-t^{-\frac{1}
{2}})(-t^{\frac{5}{2}}-t^{\frac{1}{2}})\rbrace\\\
& = & t(-t^3+t^2+1)\\\
& = & -t^4+t^3+t
\end{array}
$$
よって、右手型の三葉結び目のジョーンズ多項式は$${-t^4+t^3+t}$$と分かりました。
次に、左手型のジョーンズ多項式を求めましょう。先ほどと同じような手順と踏めば求まります。しかし、とても手間がかかるので、$${V_{L_{3,+}}(t^{-1})}$$を計算します。そうすれば、左手型のジョーンズ多項式となります。
すると、$${V_{L_{3,+}}(t^{-1})=-t^{-4}+t^{-3}+t^{-1}}$$となり、$${V_{L_{3,+}}(t)}$$と異なるので、三葉結び目は右手型と左手型があることがわかりました。
ちなみに、今回と同じように交点を選ぶ必要はなく、好きなように交点を選んでジョーンズ多項式を求めても同じ式になるはずです。
8の字結び目
では、8の字結び目のジョーンズ多項式を求めてみましょう。三葉結び目と同じ手順で求まるので今回は省略します。
結果は、
$${V_L(t)=t^2-t+1-t^{-1}+t^{-2}}$$
になるはずです。また、この鏡像は
$${V_L(t)=t^{-2}-t^{-1}+1-t+t^2}$$
となります。8の字結び目では$${V_{L}(t)=V_{L}(t^{-1})}$$となりました。ここで重要なのは、鏡像が等しいから両手型結び目であるというのは気が早いです。
ジョーンズ多項式の場合、「両手型結び目ならばその結び目のジョーンズ多項式と鏡像のジョーンズ多項式が等しい」までしか言えません。
関連の未解決問題
ジョーンズ多項式関連の未解決問題はいくつかあります。
1つ目
ジョーンズ多項式はある結び目とその鏡像の多項式が異なれば右手型と左手型があると言えました。しかし、ジョーンズ多項式も万能ではないため、交点数が異なる結び目同士で同じ多項式になる場合があります。
そこで未解決問題の内容は、「自明な結び目とジョーンズ多項式が等しい非自明な結び目は存在するか」というものです。
非自明な結び目とは自明でない結び目のことです。
2つ目
ジョーンズ多項式の注意点は、両手型結び目ならばある結び目の多項式と鏡像の多項式が等しくなるだけで、逆は言えないということでした。
そこで未解決問題の内容は、「結び目が両手型結び目であるかどうかを完全に判定する結び目不変量はあるか」というものです。
結び目不変量とは、簡単に言えば結び目を分類するための目安です。前回の交点数やアレクサンダー多項式、今回のジョーンズ多項式が結び目不変量です。
まとめ
今回はジョーンズ多項式について主に説明しました。ジョーンズ多項式でも両手型結び目を見分けるには至りませんでした。
また、結び目不変量は他にも絡み数や棒指数、結び目解消数、橋指数、本フリー多項式、ブラケット多項式の径間などがあります。
次回はこれらについて紹介していきたいと思います。
最後に
外から夕方五時の音楽が流れてきました。これはミケの帰りを呼びかけるものでもあります。
「ちょうどいいタイミングだったね。面白かった?」
「うん、興味深い! いつか万能な多項式の結び目不変量が見つかるのかなぁ」
「マロが見つけてやるさ!」
「お、それは大きく出たね。そのときにはおやつ上げる!」
ミケは半信半疑、いや一信九疑の表情を浮かべています。マロはあまり期待されていないようです。
「やった! 頑張る!」
それに気づくはずもなく、マロは気分上々でミケを見送り、頭をフル稼働させて考え始めました。
しばらくすると飼い主が帰ってきました。手にはマロが大好物のおやつを持っています。マロはそれが目に入るとこれまで考えていたことをすっかり忘れてしまい、媚びを売りに行きました。
