極方程式r＝2acosθを図から理解する

極方程式にて
C(a,0)が中心、半径aの円をr=2acosθ
と表記します。
0≦θ≦π/2 の範囲の解釈は大丈夫でしょう。円の上側になります。
では、円の下側はどう説明できるでしょうか。今回のメインテーマです。

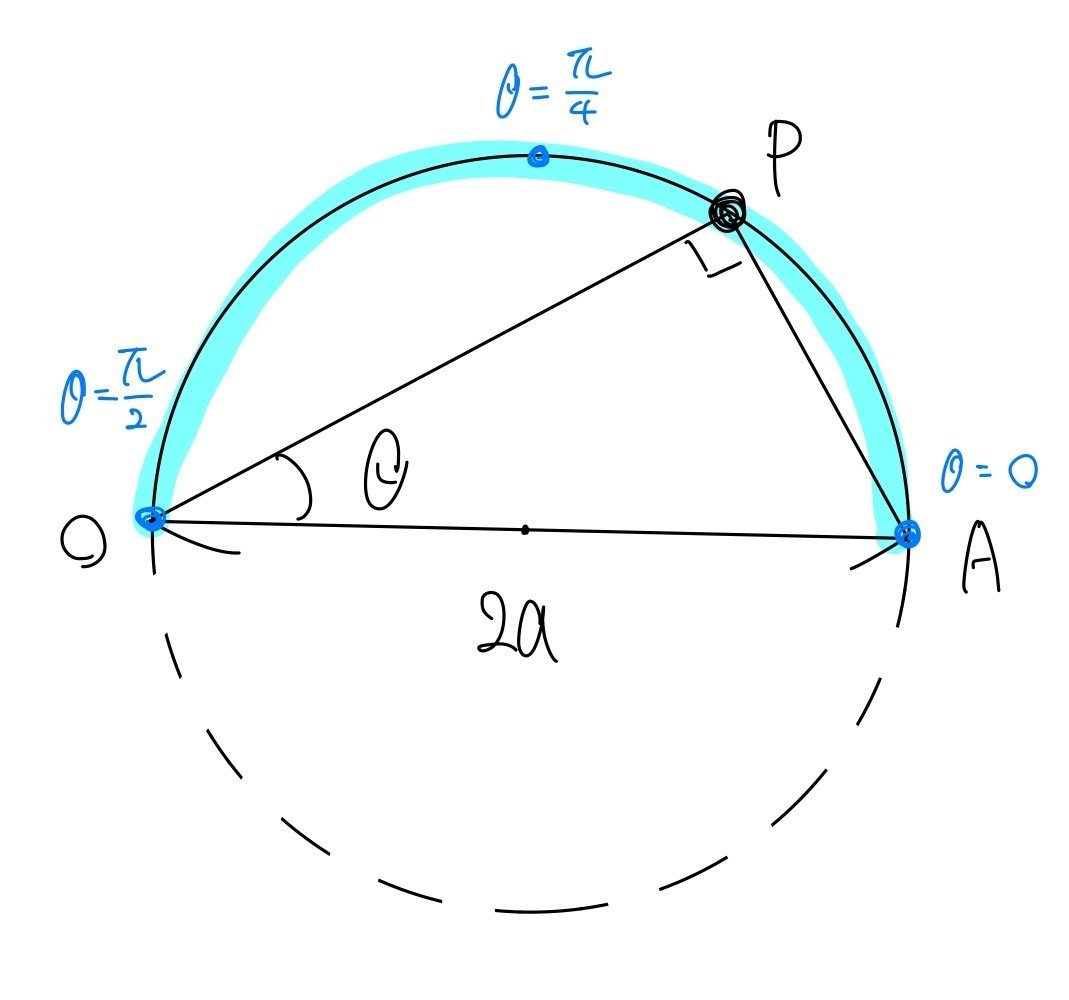
これを理解するのに大事な知識は
「極方程式の場合はrが負の値をとる場合もある」
ということです。
例えば極座標において、P(1,π/4)や(2,π/4)の様子を確認してみて下さい。これは基礎的な極座標の定義なので理解できると思います。π/4の角度を保ちながら、長さを1や2に決定していると説明が出来ると思います。

なら、(-1,π/4)はπ/4の角度を保ちながら、長さは-1に後退すると説明が出来るでしよう。(-2,π/4)も同様です。
簡単に言うなら、角度は維持したまま原点より逆側の方へ点が移動するということです。

網羅系参考書では
(r,θ)でr<0の場合は(|r|,θ+π)を表すものとする。
と書いてあります。確かにπだけ回転してあげれば示したい点と同じ点を示すことが出来るのでこの考え方は受け入れやすいでしょう。

この解釈を使えば先程の問題は解決できます。本題に戻ります。

r=2acosθで、θ＞π/2となった時、cosは負の値を取ります。aは長さであり正の値を取るので、rも負の値を取ります。
なので、Pはθの角度を保ちながら極を中心に点対称に移動した円の下側に来るわけです。
よって、円の下側もしっかり満たされることになります。

以上です。解決になれば幸いです。

【追加情報】
θで区切ると
0≦θ≦π/2→円の上側
π/2≦θ≦π→円の下側
π≦θ≦3π/2→円の上側
3π/2≦θ≦2π→円の下側
を示します。