へやわけのMX値の話(四方壁の場合)
誰もまとめてなかったのでこっち読んだ方がいいです(大体同じことが書いてあります)↓
0 前提知識
0.1 MX値
へやに入る黒マスの数の最大値を MX 値と呼びます。数式中では基本的に $${MX}$$ と書きます。
0.2 ペナルティ理論
ペナルティ理論とは、「黒マスを充填する際、最も効率の良い充填と比べてどれだけ損をしているか」を定量的に表すことを目的とした理論です。この指標のことをペナルティと呼びます。
ペナルティには第一種、第二種、第三種の三種類が存在します。概略は以下の通りです。
第一種:角のマスを黒マスにしないことによるペナルティ
第二種:外周に黒マスを詰め込まないことによるペナルティ
第三種:白マスによるループができることによるペナルティ
特に第三種ペナルティに関しては、「空中の黒マスがアースしないことによるペナルティ」と言い換えることができます。
この定義は主に [1] に依っています。詳細は [1] [3] [4] などをご参照ください。
0.3 総ペナルティとペナルティ許容量
へやが全て白マスのときのペナルティの数を総ペナルティと呼びます。数式中では基本的に $${P}$$と書きます。
$${m, n \ge 3}$$ のとき、$${m \times n}$$ の盤面の総ペナルティは次式のようになります。
$$
P = mn + \begin{cases}
1 &\text{($m, n$ がともに偶数)}\\
2 &\text{($m, n$ の一方のみが偶数)}\\
3 &\text{($m, n$ がともに奇数)}
\end{cases}
$$
また、へやに黒マスを置いた後に残るペナルティの数をペナルティ許容量 (penalty tolerance) と呼びます。数式中では基本的に $${T}$$ と書きます。
ペナルティ許容量はへやの総ペナルティと黒マスの数によって決まる量です。具体的には、へやに入れる黒マスの数を $${K}$$ としたとき次式が成り立ちます。
$$
T = P - 3K
$$
これを変形すると、
$$
K = \dfrac{P - T}{3} \le \left\lfloor \dfrac{P}{3} \right\rfloor
$$
を得ます。ここで最右辺はへやの形にのみ依存して決まることから、この式は MX 値の上界を与えていると解釈できます。
また、$${T \le 2}$$ のときは上式で等号が成り立ちます。このことから、ペナルティが 2 以下になるようにへやに黒マスを置くことができれば、それが最密充填であることが自動的に分かります。
0.4 空中のへやのペナルティ
空中のへやにおける総ペナルティは第三種ペナルティを数えることによってわかります。具体的な例として、 $${m \times n}$$ のへやでは
$$
P = (m+1) (n+1) = mn + m + n + 1
$$
となります。
ところが、この値によってペナルティ許容量を計算すると、実際にへやの内部で発生するペナルティより 1 多くなります。これはへや自体がアースしていないことによる第三種ペナルティが発生しているからです。そこで、空中のへやの場合は便宜上 $${P - 1}$$ を総ペナルティとし、この値を元にしてペナルティ許容量を計算することにします(この辺をきちんと議論した記事を見たことがないので、あれば教えてください)。
このとき、$${m \times n}$$ のへやにおけるペナルティ許容量と [2] で定義されている余裕値 $${R}$$ には次の関係が成り立ちます。
$$
T = \begin{cases}
R & \text{($mn$が奇数のとき)} \\
R + 2 & \text{($mn$が偶数のとき)} \\
\end{cases}
$$
実際、しまつぶし第一公式([2, 定理 1-2])を具体的に書き換えることでこれが得られます。
1 幅 1 の場合
盤面サイズが $${1 \times n}$$ の場合の MX 値は明らかに、
$$
MX = \begin{cases}
1 & (n = 1, 2)\\
2 & (n \ge 3)
\end{cases}
$$
となります。

2 幅 2 の場合
$${2 \times n}$$ の盤面において図 2.1 のような分割充填を考えると、分割されたそれぞれの領域において黒マスは高々 1 個しか入りません。よって MX 値は、
$$
MX = \left\lceil \dfrac{n}{2} \right\rceil
$$
となります。

3 幅 3 の場合
$${3 \times n}$$ の盤面は以下のような充填を持ちます。

このときペナルティは、 $${n}$$ が奇数のとき 0、偶数のとき 2 となり、いずれにせよ最密充填であることがわかります。
このときの MX 値は、
$$
MX = \begin{cases}
n + 1 & (\text{$n$ が奇数}) \\
n & (\text{$n$ が偶数})
\end{cases}
$$
となります。
4 幅 4, 5, 7 の場合
長くなりそうなのでやる気が出たら別記事で書きます冒頭で紹介したSP1氏の記事に全部載ってます。Tobo 定理の説明だけ記事を書くかもしれません。
5 幅 6 の場合
5.1 6 × 偶数の場合
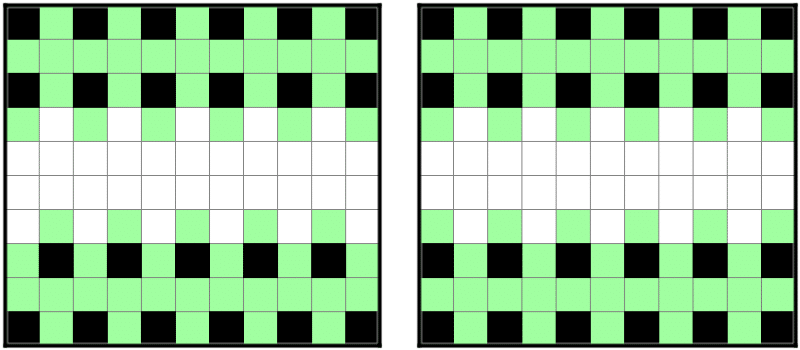
6 × 6 の盤面は以下のような最密充填を持ちます。

ペナルティが 1 であることから、確かにこれは最密になっています。
ここで赤くハイライトした部分は 2 マスずつ延長でき、このような延長によって新たに分断もペナルティも増えないので、これは最密充填になっています。
よって一般の 6 × 偶数の場合もそのような延長は最密となり、MX 値は
$$
MX = \dfrac{P - 1}{3}
$$
となります。
5.2 6 × 奇数の場合
6 × 7 の盤面は以下のような最密充填を持ちます。

ペナルティが 1 であることから、確かにこれは最密になっています。
ここで赤くハイライトした部分は 2 マスずつ延長でき、このような延長によって新たに分断もペナルティも増えないので、これは最密充填になっています。
よって一般の 6 × 奇数の場合もそのような延長は最密となり、MX 値は
$$
MX = \dfrac{P - 1}{3}
$$
となります。
以下特記の無い限りへやのサイズは 8 以上とします。
6 偶数×偶数の場合
6.1 8 × 8 の場合
8 × 8 の盤面は以下のような最密充填を持ちます。

ペナルティが 2 であることから、確かにこれは最密になっています。
6.2 8 × 10 の場合
8 × 10 の盤面は以下のような最密充填を持ちます。

ペナルティが 0 であることから、確かにこれは最密になっています。
6.3 10 × 10 の場合
10 × 10 の盤面は以下のような最密充填を持ちます。

ペナルティが 2 であることから、確かにこれは最密になっています。
6.4 一般の場合
前節までで示した幅 6, 8, 10 の最密充填の右辺および下辺を見ると、黒マスの配置が以下のいずれかの形になっています。

このいずれの配置に対しても、以下のような 6 マスの延長が存在します。

このような延長によって新たに分断もペナルティも増えないので、これは最密充填になっています。
また、このように延長した黒マスは配置が再び図 6.4 のようになっているので、図 6.5 の延長を繰り返すことができます。
さらに、図 6.4 および図 6.5 において赤くハイライトした部分は 2 マスずつ延長(または削除)することができるので、任意の偶数 × 偶数の場合についても図 6.5 と同様の延長が存在することがわかります。
以上の議論より任意の偶数 × 偶数の場合について、3 で割った余りで類別することで辺の長さが 6, 8, 10 のいずれかの場合に帰着できます。そのときのペナルティ許容量はいずれの場合も 2 以下であったことから、MX 値は
$$
MX = \left\lfloor \dfrac{P}{3} \right\rfloor
$$
となります。
7 奇数 × 奇数の場合
7.1 一般の場合
奇数 × 奇数の盤面で第一種および第二種ペナルティを発生させないように外周に黒マスを充填したとき、盤面は図 7.1 のようになります。

このとき白マスのループがひとつできていることから、最密充填におけるペナルティ許容量の下限は 1 となります。また、これによりペナルティが 3 以下になる黒マス配置は最密充填となります。
ここで再び図 7.1 に注目すると、上下左右の各 2 列を除いた部分は(アースの無い)空中のへやと見做せます。空中のへやのMX値とその際に生じるペナルティについては以下が成り立つことが知られています。
タテヨコのいずれかの長さが $${6n + 5}$$ のとき、ペナルティが 2 であるような最密充填が存在する。
$${(6m + 1) \times (6n + 3)}$$ のとき、ペナルティが 1 であるような最密充填が存在する。
$${(2^n - 1) \times (2^n - 1)}$$ のとき、ペナルティが 0 であるような最密充填が存在する。
それ以外の $${(6m + 1) \times (6n + 1)}$$ および $${(6m + 3) \times (6n + 3)}$$ の場合はペナルティが 3 であるような最密充填が存在する。
詳しくは [2, §3] をご参照ください。
よって、上下左右の各 2 列を考慮に入れると、タテヨコのいずれかの長さが $${6n + 3}$$ のとき、$${(6m + 1) \times (6n + 5)}$$ および $${(2^n + 3) \times (2^n + 3)}$$ のときは、
$$
MX = \left\lfloor \dfrac{P - 1}{3} \right\rfloor
$$
となります。
7.2 11 × 11 の場合
以下の節では、前節で除外した場合について考察します。
11 × 11 の盤面は以下のような最密充填を持ちます。

ペナルティが 1 であることから、確かにこれは最密になっています。
7.3 13 × 13 の場合
13 × 13 の盤面は以下のような最密充填を持ちます。

ペナルティが 1 であることから、確かにこれは最密になっています。
7.4 一般の (6m + 1) × (6n + 1) および (6m + 5) × (6n + 5) の場合
前節までで示した幅 11, 13 の最密充填の右辺および下辺を見ると、黒マスの配置が以下の形になっています(灰色はあってもなくても良い黒マス)。

このような配置に対して、以下のような 6 マスの延長が存在します。

このような延長によって新たに分断もペナルティも増えないので、これは最密充填になっています。
また、このように延長した黒マスは配置が再び図 7.4 のようになっているので、図 7.5 の延長を繰り返すことができます。
さらに、図 7.5 において赤くハイライトした部分は 2 マスずつ延長(または削除)することができるので、任意の奇数 × 奇数の場合についても図 7.5 と同様の延長が存在することがわかります。
以上の議論より任意の $${(6m + 1) \times (6n + 1)}$$ および $${(6m + 5) \times (6n + 5)}$$ の場合について、辺の長さが 11, 13 のいずれかの場合に帰着できます。そのときのペナルティ許容量はいずれの場合も 1 であったことから、MX値は
$$
MX = \dfrac{P - 1}{3}
$$
となります。
8 偶数 × 奇数の場合
8.1 解の延長
今、偶数 × 奇数の盤面の黒マスの最密充填において、右辺と下辺の黒マスの配置が以下の形になっているとします。

このとき、このような配置に対して、以下のような 3 マスの延長が存在します。

このような延長によって新たに分断もペナルティも増えないので、これは最密充填になっています。
さらに、図 8.1 および図 8.2 において長さが偶数の辺を見ると、黒マスの配置が 6.4 節の図 6.4 のようになっています。また長さが奇数の辺を見ると、黒マスの配置が 7.4 節の図 7.4 のようになっています。
よっていずれの方向にも 6 マスごとの延長が存在し、このような延長によって新たに分断もペナルティも増えないので、これは最密充填になっています。
以上より、図 8.1 のような最密充填が存在する場合、その盤面よりも大きく、タテヨコの長さを 3 で割った余りが同じ組み合わせになるような全ての盤面についてペナルティを増やすことなく最密充填を与えることができます。
8.2 タテヨコのいずれかが 3 の倍数の場合
6 × 奇数の場合の最密充填(5.2 節参照)を見ると、黒マスの配置が図 8.1 のようになっています。よって 8.1 節の議論により、タテヨコのいずれかが 3 の倍数の場合について、ペナルティが 2 であるような最密充填が得られます($${6n \times 7}$$ の場合についてはこの限りでないことに注意。6 × 7 の場合の黒マスの配置は 7.4 節の延長の条件を満たさないため、同様の議論ができない)。
よってこの場合のMX値は
$$
MX = \dfrac{P - 2}{3}
$$
となります。
8.3 (3m + 1) × (3n + 2) の場合
7 × 8 の盤面は以下のような最密充填を持ちます。

ペナルティが 1 であることから、確かにこれは最密になっています。
また、これは黒マスの配置が図 8.1 のようになっています。よって 8.1 節の議論により、一般の $${(3m + 1) \times (3n + 2)}$$ の場合について、ペナルティが 1 であるような最密充填が得られます($${(6n + 2) \times 7}$$ の場合についてはこの限りでないことに注意。7 × 8 の場合の黒マスの配置は 7.4 節の延長の条件を満たさないため、同様の議論ができない)。
よってこの場合のMX値は
$$
MX = \dfrac{P - 1}{3}
$$
となります。
8.4 (6m + k) × (6n + k + 3) の場合のための準備
$${(6m + k) \times (6n + k + 3),\quad k = 1, 2}$$ と書けるような盤面において総ペナルティを考えます。このとき、$${k^2 \equiv 1 \pmod 3}$$ より、
$$
P = (6m + k) (6n + k + 3) + 2 \equiv k^2 + 2 \equiv 0 \pmod 3
$$
となるので、総ペナルティは 3 の倍数になります。すなわち、ペナルティ許容量が 0 であるような最密充填が存在する可能性があるということです。そこで、本節ではそのような最密充填の満たすべき条件を考察します。
まず、上記の盤面においてペナルティ許容量が 0 であるとします。このとき、第一種および第二種ペナルティを考えると以下がすぐに決まります。

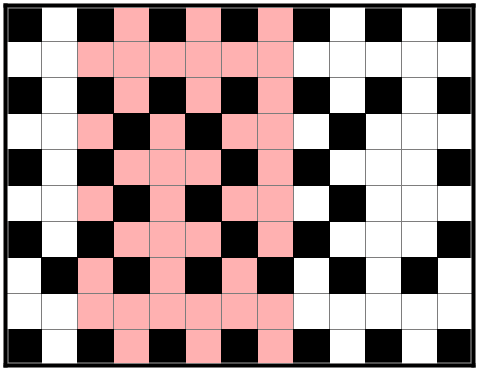
また、左辺および右辺における黒マスの入れ方を考えると、対称性より黒マスの配置は以下の図 8.5、またはその反転になります。

ここで下辺における第三種ペナルティが生じないような黒マスの入れ方は以下の二通りです。
このうち左の配置が必ずハタンすることを示します。
まずペナルティ理論により決定するところを全て進めると、以下のようになります。

ここで盤面に左上を $${(1, 1)}$$ とする座標を入れ、座標の偶奇が一致するマスを A 面、そうでないマスを B 面とします(すなわち市松模様に塗り分けます)。

このとき図 8.7 を見ると、空中の黒マスがアースできるような辺の黒マスは A 面にしか存在しません。ペナルティ許容量が 0 であるという条件から全ての黒マスはアースしなければならないので、全ての空中の黒マスは A 面に存在することが分かります。

ここで盤面を以下のように領域 α、β、γ に分割することを考えます。

このとき、白マス分断禁より領域 α の白マスと領域 γ の白マスは領域 β を経由して接続しなければなりませんが、以下に示すようにそれは不可能です。
まず、A 面のうち座標が (奇数, 奇数)であるマスを A1 面、座標が (偶数, 偶数) であるようなマスを A2 面と呼ぶことにします。このとき、白マスを結ぶ経路が領域 α から領域 β に入るときのことを考えると、これは必ず最初に A2 面の白マスを通ります。一方で、領域 γ から領域 β に入るときは、必ず最初に A1 面の白マスを通ります。
よって、領域 β 内で A1 面の白マスと A2 面の白マスを結ぶ経路が存在することになります。すなわち A1 面~B 面~A2 面と繋がった白マスが存在することになりますが、そのような白マスがあったとすると第三種ペナルティが生じます。これはペナルティ許容量が 0 であることに矛盾します。
ゆえに領域 α の白マスと領域 γ の白マスは分断され、ハタンしてしまうことが分かりました。これが初めに示したかったことでした。
以上よりペナルティ許容量が 0 であるような黒マス配置があったとすると図 8.6 の右の配置に限ることが分かりました。さらに対称性を考えると、以下の黒マスが決まります。

ここでペナルティ許容量 0 という条件より、A 面および B 面の黒マスはアースする必要があります。一方、盤面全体で黒マスがアースできる箇所は左右辺の二箇所しか無く、このうち A 面は既に左辺でアースしています。よって B 面の黒マスは右辺でアースする必要があります。
以上の結果を用いて、幅 8 および 10 の場合を考察していきます。
8.5 8 × (6n + 5) の場合
$${8 \times (6n + 5)}$$ の盤面でペナルティ許容量が 0 であるとします。このとき、盤面の左 5 マスに注目すると、8.4 節の考察より以下が決まります。

しかし、このとき A 面の黒マスを左辺にアースしつつ B 面の黒マスを右辺にアースすることは明らかに不可能です。よってペナルティ許容量が 0 であるような黒マス配置は実現できないことが分かりました。
一方で、同じ盤面において以下のようなペナルティが 3 であるような充填が存在します。

この配置において赤くハイライトした部分は 6 マスずつ延長することができます。
よって MX 値は、
$$
MX = \dfrac{P - 3}{3}
$$
となります。
8.6 10 × (6n + 1) の場合
$${10 \times (6n + 1)}$$ の盤面でペナルティ許容量が 0 であるとします。このとき、盤面の左 7 マスに注目すると、8.4 節の考察より以下が決まります。

さらに黒マスのアースに関する議論により、以下の図 8.15 までが決まります。

しかし、赤く囲った領域のどちらに黒マスを入れたとしても、以下のようにすぐにハタンします。

よってペナルティ許容量が 0 であるような黒マス配置は実現できないことが分かりました。
一方で、同じ盤面において以下のようなペナルティが 3 であるような充填が存在します。
この配置において赤くハイライトした部分は 6 マスずつ延長することができます。
よって MX 値は、
$$
MX = \dfrac{P - 3}{3}
$$
となります。
8.7 一般の (6m + 2) × (6n + 5) の場合
11 × 14 の盤面は以下のような最密充填を持ちます。

ペナルティが 0 であることから、確かにこれは最密になっています。
ここで左辺においては 7.4 節の図 7.5 のような 6 マスごとの延長が存在します。
また、下辺においては下図のような 6 マス毎の延長が存在します。

このような延長によって新たに分断もペナルティも増えないので、これは最密充填になっています。
また、このように延長した黒マスは下辺の配置が再び図 8.17 のようになっているので、図 8.18 の延長を繰り返すことができます。
さらに図 8.18 において赤くハイライトした部分は 2 マスずつ延長(または削除)することができるので、任意の $${(6m + 2) \times (6n + 5),\ m \ge 2,\ n \ge 1}$$の場合についても図 6.5 と同様の延長が存在することがわかります。
よって MX 値は、
$$
MX = \dfrac{P}{3}
$$
となります。
8.8 一般の (6m + 1) × (6n + 4) の場合
13 × 16 の盤面は以下のような最密充填を持ちます。

ペナルティが 0 であることから、確かにこれは最密になっています。
ここで左辺においては 7.4 節の図 7.5 のような 6 マスごとの延長が存在します。また、下辺においても図 8.18 のような 6 マス毎の延長が存在します。
よって MX 値は、
$$
MX = \dfrac{P}{3}
$$
となります。
参考文献
[1] まり餡氏のツイート(ツリー)
[2] 超へやわけMX(ウェブアーカイブ)
[3] ペナルティへやわけ - にしなん記録室
[4] Teal's Mini Heyawake Guide
