【モンテカルロ法】円周率の近似計算

モンテカルロ法を用いて円周率の近似計算を行いました！

概要

一辺の長さが 2 の正方形に内接する半径 1 の円を考えましょう。この正方形の内部に"ランダムに"点を打つと、その点が内接円の内部にある確率は、

となります。以下の記事が詳しいです。

モンテカルロ法と円周率の近似計算 | 高校数学の美しい物語

このことから、円周率の近似計算を行うことができます。

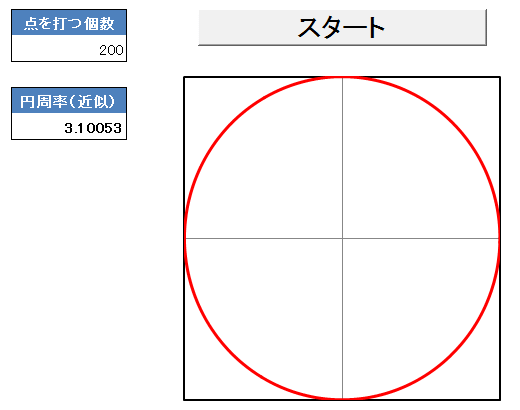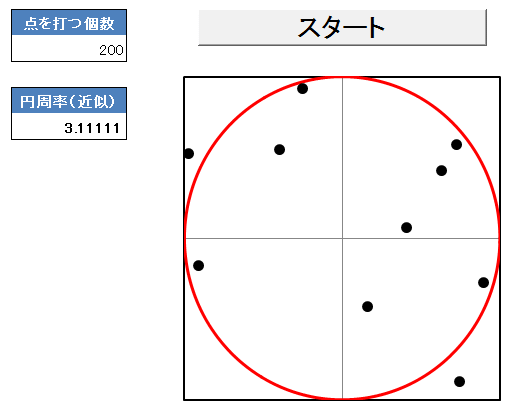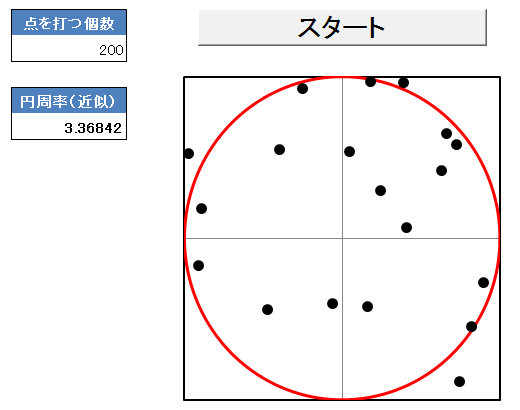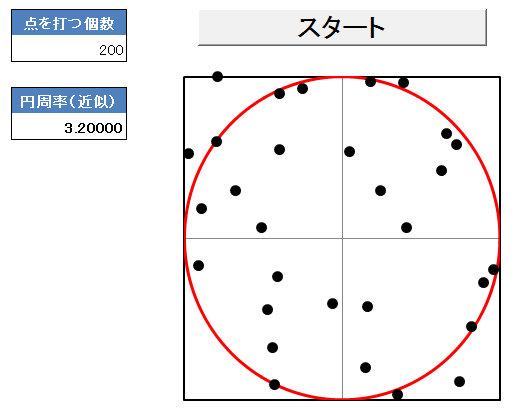
シミュレーション

実際に点を打って、シミュレートした結果を下に示します！

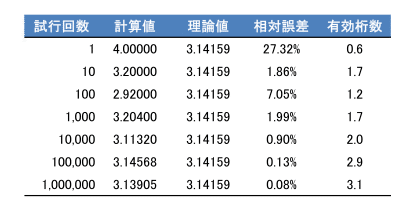
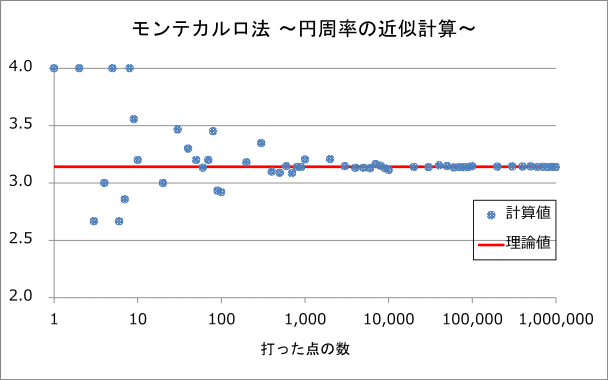
結果

点を増やすことで、3.14......に収束していく様子が見れました。
ゆとり教育を脱出するには、100万点くらい必要でした。

エクセルとVBA

使ったエクセルとVBAのコードです。

PI.xlsm

224 KB

ファイルダウンロードについて

ダウンロード

Option Explicit

Sub simu()
   Dim i As Long
   Dim N As Long
   Dim count As Long
   Dim x As Double
   Dim y As Double

   N = Range("N_")
   count = 0
   
   Columns("AD:AE").Clear
   
   For i = 1 To N
       Call 点を打つ(x, y)
       
       If x * x + y * y < 1 Then
           count = count + 1
       End If
       
       Cells(i, "AD") = x
       Cells(i, "AE") = y
       
       ActiveSheet.ChartObjects("グラフ 2").Activate
       ActiveChart.SeriesCollection(2).XValues = "=" & Range("AD1", Cells(Rows.count, "AD").End(xlUp)).Address(True, True, , True)
       ActiveChart.SeriesCollection(2).Values = "=" & Range("AE1", Cells(Rows.count, "AE").End(xlUp)).Address(True, True, , True)
       
       DoEvents
       
       With Range("PI_")
           .NumberFormatLocal = "0.00000"
           .Value = count / i * 4
       End With
   Next i
   
End Sub

Sub 点を打つ(ByRef x As Double, ByRef y As Double)
   x = 2 * Rnd - 1
   y = 2 * Rnd - 1
End Sub

―――――記事はここまで―――――
最後まで読んでくださり、ありがとうございました！