10年ぶりのプログラム「引退したプログラマーがPythonでAIプログラミングに挑戦する」-08:開発_コマごとのルール作成
コーディングの方針
1つのコマが複数の場所に移動できることが多いです。
たとえば、ルークでいえば、自分の前方にコマがなければ、一番下から一番上まで進めます。つまり移動可能先としては、row=6,row=5,,,,row=0となります。
これら複数の移動可能先を、get_Rook_movesのリターン値として取得する場合には、この関数を複数回呼び出す必要があります。それは避けたいので、呼び出す関数の引数にoutput変数を使います。そして関数の中でそのoutput変数に移動可能先を追加していくこととします。
説明の方針
これから
ポーン
ナイト
ビショップ
ルーク
クイーン
キング
の順番でコーディングをしていきます。
コーディングをする前に、コマの動き(ルール)を説明し、その後でコーディングを行います。
ポーン
ルール
将棋の歩の動きに似ている部分が多いです。
前に進むことはできますが、戻ることはできません。プログラム的にいうと、
・白のときには、rowが小さくなる。
・黒のときには、rowが大きくなる。
ということです。
ただし、相手のコマと正面衝突したときには、それ以上前に進むことができません。将棋と違って、目の前のコマをとることができないのです。なので、チェスではよく下記のような場面になります。これらのポーンはすべて、動くことができません。

ではポーンはコマをとることができないのか?というとそうではありません。自分の斜め前の駒をとることができます。左右どちらでもとれます。

ポーンが前に進むとき、Colは一定です。Rowが変わります。
ポーンが斜めに進むとき、ColとRowの両方が変わります。
またポーンは、自分が最初の位置にいるときにのみ、2マス前に進むことができます。もちろん1マスでもかまいません。どちらでもいいです。

プログラム的には、rowが最初の値とおなじだったら、2マス動くことも可能、ということになります。
コーディング
get_Pawn_moves
このポーンの動きをコーディングしていきます。
ポーンの場合には、白か黒かによって、動きが制限されます。
白:Rowが小さくなる
黒:Rowが大きくなる
ゆえにコマの色をつかって変数を指定します。

最初に、まっすぐ前に進む場合のコーディングをします。
ボードの外にでないように、rowには制限を常に設けます。つまり一番上あるいは下にいるときには、移動はできないようにrow>0 and row<7という制限をつけます。なお、この制限はコマをとる場合にも適用されます。
自分の目の前のコマを取れないので、移動場所が空欄の場合にのみ移動可能となります。これをifで表現しています。
また、最初のときには2つ動かすこともできるので、それも記述します。

次にコマをとるときの動きです。
斜めに動くので、ボードの外にでないようにColにも制限をかけます。つまり、
Colが小さくなるときには、Col-1>0
Colが大きくなるときには、Col+1<7
という制限です。
斜め前に敵のコマがあるときだけ、動けます。if文でそれを表現しています。

全体では下記のようになります。

get_all_possible_moves
この関数が呼ばれるように、get_all_possible_movesを変更します。

動きを確認して、OKでしたら次に進みます。
ナイト
ルール
いわゆる桂馬飛びをします。将棋とは異なり、8方向すべてに飛べます。もちろん、ボードの外には出られません。

コーディング
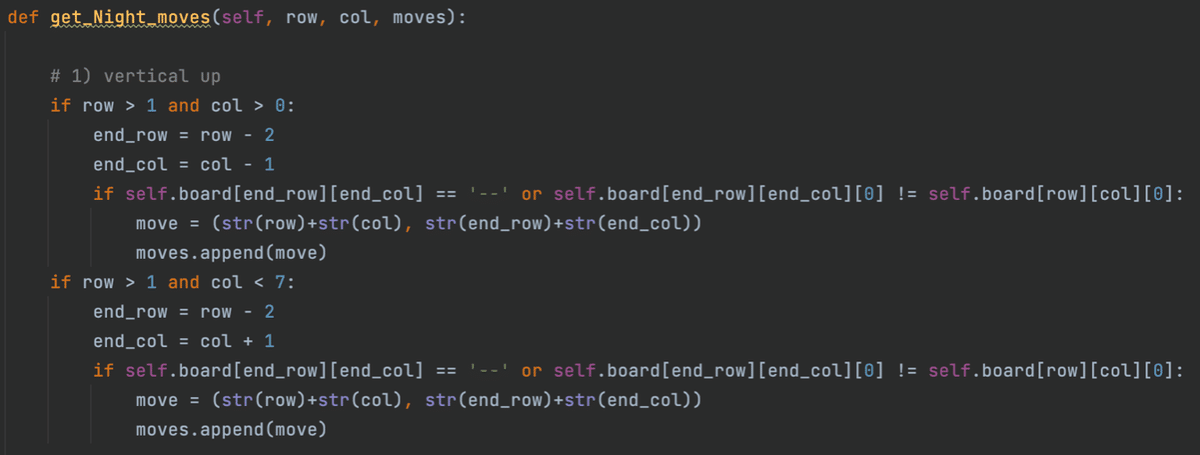
get_Night_moves
前後に動くときには、Rowが2つ、Colが1つ動く
左右に動くときには、Rowが1つ、Colが2つ動く
という動きをします。
また動いた先が自分の色の場合、そのマスには移動できません。
上記を、動く方向を4つに分けてコーディングをしました。




get_all_possible_moves
この関数が呼ばれるように、get_all_possible_movesを変更します。

動きを確認して、OKでしたら次に進みます。
ビショップ
ルール
ビショップは、将棋の角に相当します。
つまり左右の斜め方向に、どこまでも動かすことができます。ただし、途中にコマがあったらそれより先にはいけません。
そのコマが
・同じ色のコマの場合、そのコマをとれないので、その手前まで移動できます。
・違う色のコマの場合、そのコマをとれるので、その位置まで移動できます。

コーディング
get_Bishop_moves
ビショップは自分から見て、右前・左前・右下・左下に動けます。ナイトのときと同様に、動ける方向を4つに分けてコーディングをします。

1番目のエリアの場合
これは白番にとっては右上に移動、黒番にとっては左下に移動ということです。どちらの場合でも、Rowが小さくなり、Colが大きくなる方向に進みます
自分の移動可能範囲に別のコマがいるか否かに応じて結果が異なります。コマがいなければボードの端までいけますが、コマがあったらそこで移動が止まります。これをLoopとbreakを使って表現します。もちろん、ボードの外に出ないような配慮が必要です。
Range関数
Range関数の引数について説明します。次のルークでも使用します。
1番目の引数は、スタート位置
2番目の引数は、ゴールの手前の位置(つまりその数字は含みません。)
3番目の引数は、増減値(1づつ増やすときには省略可能)
となっております。
今回はRowが小さくなる移動です。Row=0がゴールですので、-1を2番目の引数としています。

残りのエリアについても同様です。



get_all_possible_moves
この関数が呼ばれるように、get_all_possible_movesを変更します。

動きを確認して、OKでしたら次に進みます。
ルーク
ルークは、メジャー・ピースと呼ばれるとても強いコマです。
ルール
将棋の飛車に相当します。縦横に動けます。ただし、ビショップと同様に、味方がいたらその手間のマスまで、敵がいたらそのマスまでの移動となります。

コーディング
get_Rook_moves
基本構造はビショップと同じです。4つのエリアに分けてコーディングします。





get_all_possible_moves
この関数が呼ばれるように、get_all_possible_movesを変更します。

動きを確認して、OKでしたら次に進みます。
クイーン
最強のコマです。
ルール
動きとしては、ビショップとルークの動きを足したものになります。

コーディング
get_Queen_moves
単純にget_Bishop_movesとget_Rook_movesを呼び出すだけです。

get_all_possible_moves
この関数が呼ばれるように、get_all_possible_movesを変更します。

動きを確認して、OKでしたら次に進みます。
キング
ルール
将棋の王将と同じです。前後左右斜めに1マス動けます。

コーディング
get_King_moves
前方、後方、左右の3エリアにわけてコーディングをしています。
他のコマと同様に、
同じ色のコマの場所には移動できません。
ボードの外には出られません。




get_all_possible_moves
この関数が呼ばれるように、get_all_possible_movesを変更します。

動きを確認して、OKでしたら今回はこれで終わりにします。
使用しているチェスのコマは、下記からダウンロードしました。
By jurgenwesterhof (adapted from work of Cburnett) - http://commons.wikimedia.org/wiki/Template:SVG_chess_pieces, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=35634436
この記事が気に入ったらサポートをしてみませんか?
