
時系列解析(分析)とは|概要やメリット、モデル、進め方、事例を紹介
こんにちは。スキルアップAI編集部です。時系列解析は、時間の経過にともなうデータ変化を分析する統計手法であり、過去のデータから未来の動向を予測するために用いられます。金融やマーケティング、セキュリティなど多岐にわたる分野で応用されており、重要性が高まっています。
本記事では、時系列解析の概要、代表的なモデルと具体例、用いられるツール、勉強方法などを紹介していきます。
時系列解析(分析)とは
時系列解析は、ある現象の時間変動を捉えるために、時系列データを分析する方法です。(「時系列分析」とも呼ばれます。)時間の経過順に並んだデータを対象に、統計的な手法を用いて「長期的な傾向」や「周期的な変化」、「それらとは異なるノイズ」などの成分に分解し、将来の値を予測します。

時系列解析は、時系列データに潜む傾向や特徴を把握したり、時系列データの将来の値を予測したりする際に有効な技術です。
時系列データとは
時系列データとは、時間的な順序をともないながら観測されるデータのことです。ある一定の時間間隔で観測されたデータや、イベントが発生した時刻・頻度などが含まれます。以下が時系列データの一例です。
株価データ
天気予報の気温や降水量などの気象データ
人口統計データ
センサーデータ
音声データ
販売数データ
回帰分析との違い
回帰分析は、データの属性間の関係式を求める分析手法です。未知の状況における予測など、データが時間的に独立している場合に用いられます。例えば、身長と体重の関係を線形回帰モデルでモデル化することで、身長から体重を予測できます。
一方、時系列解析は、時間的に連続するデータに対して解析を行う手法です。時間に依存するトレンド、周期性、季節性、ノイズ(分析に必要とされない情報)などの要素をモデル化し、未来の値を予測することが目的です。例えば、過去の株価データを用いて、将来の株価を予測することが挙げられます。
時系列解析は、過去のデータが未来の値に影響を与える「自己相関性」を考慮し、時間的なパターンを分析する手法です。一方、回帰分析は変数間の相関関係をモデル化し、線形関係を前提とした予測や解釈を行います。
時系列解析のメリット
時系列解析には次のようなメリットがあります。
将来予測が可能
モデルの評価が可能
データの不均一性を扱える
それぞれ説明していきます。
・将来予測が可能
売上金額や来客数、広告クリックなどのデータを用いて、ビジネスシーンにおけるさまざまな分野で将来予測することができます。
・モデルの評価が可能
過去のデータを用いて予測を行い、実際の値と比較することで、モデルの精度を測ることが可能です。これによって、効率的にモデルの改善を行えます。
・データの不均一性を扱える
時系列解析では、データの不均一性を考慮した分析が可能です。例えば、月ごとのデータと日ごとのデータを同時に扱うことができます。
時系列解析の活用シーン
時系列解析の活用シーンを3パターンに分けて紹介します。
将来予測
効果推定
異常検知
将来予測
商品需要予測に基づいて生産量を最適化したい場合に、時系列データである「商品の販売履歴」を用いて時系列解析を行います。商品の生産量調整といった経営判断を行う場合、予測の信頼性や根拠が必要となります。
そのような予測値や予測の根拠を知りたいときに、時系列解析が用いられます。
効果推定
マーケティング施策の効果検証にも時系列解析を用いることができます。ウェブサイトにおける「ユーザログ情報やSNSデータ」は時系列データです。マーケティング施策の効果を検証する際は、施策前後の変化を分析する必要があります。
そのような時間方向の変化をとらえたいときに、時系列解析が用いられます。
異常検知
異常検知にも時系列解析を適用することができます。例えば、製造工場で取得されるセンサデータは時系列データです。工場ラインで異常が発生する前には、何らかの兆しがみられることがあります。
そのような兆しをとらえたいときに、時系列解析が用いられます。
時系列データの変動要因
時系列解析で扱う時系列データは、大きく5つの変動要因に分解することができます。
長期(傾向)変動
循環変動
季節変動
周期変動
不規則変動
長期(傾向)変動
長期変動とは、長期にわたる持続的な変動のことを指し、データの値が時間の経過とともに長期的に増減するようなパターンを示します。長期変動は、数年から数十年以上にわたる期間で現れることがあります。長期変動を把握することで、将来の傾向を予測することができます。例えば、株価や気象データなどがあります。
循環変動
循環変動は、一般的に3〜15年くらいのある一定の周期で現れる変動のことで、長期的なサイクルや経済の景気循環に応じてデータが変動することを指します。ビジネスサイクルや株式市場の変動は循環変動の例として挙げられます。
季節変動
季節変動は、季節ごとに繰り返される変動です。季節変動は、1年間(12か月間)の中で定期的に発生するパターンやトレンドです。たとえば、気温、売上、旅行需要など、季節的な要素に影響を受けるデータが挙げられます。このように、年単位の周期性をもつことが一般的です。
周期変動
周期変動は、データが特定の周期をもって変動することを指します。ただし、季節変動や循環変動とは異なり、より一般的な周期性を示します。例えば、月次、週次、日次など、より短い期間において周期的に変動するデータが挙げられます。
不規則変動
不規則変動は、上記の長期変動や周期変動では説明できない変動を指します。会社の不祥事における株価暴落や地震や台風を含む自然災害など、明確に説明できない偶然起こった変動のことです。
時系列解析の3つのアプローチ方法
時系列解析のアプローチ方法として本記事では3つのアプローチ方法を紹介します。
1. 自己回帰系モデルから入る
自己回帰系モデルは、時系列の将来値を過去の値の関数であると仮定します。代表的な自己回帰系モデルは以下のようなものがあります。
ARモデル(自己回帰モデル)
ARモデル(Auto Regressive)は、過去の値の線形和で表されるモデルです。ARモデルは、自己相関が存在するデータの場合に有効です。
MAモデル(移動平均モデル)
MAモデル(Moving Average)は、ホワイトノイズ(期待値が常に0、分散が常に一定、自己相関をまったくもたない系列)の線形和で表されるモデルです。MAモデルは、現在のデータに対する過去の予測誤差の影響を考慮しながらデータ推移を予測します。
ARMAモデル(自己回帰移動平均モデル)
ARMAモデル(Auto Regressive Moving Average)は、ARモデルとMAモデルを組み合わせたモデルです。ARモデルとMAモデルを組み合わせることで、自己相関性の強い時系列データとランダムな変動を両方表現できるため、幅広い時系列データに適用できます。
しかし、ARMAモデルは、時系列データが定常的であることを前提にしているため、非定常なデータには適用できません。
ARIMAモデル(自己回帰和分移動平均モデル)
ARIMAモデル(Auto Regressive Integrated Moving Average)は、ARMAモデルに I(和分過程)を加えたモデルです。和文過程とは、英語でIntegratedといい、モデルに当てはめる時系列の階差を何回とれば定常になるかを指すものです。
前述の通り、時系列データが非定常な場合、ARMAモデルを適用できません。そのため、ARIMAモデルでは、差分を取ることによって定常過程に変換し、ARMAモデルを適用可能な形に変換します。
SARIMAモデル(季節変動自己回帰和分移動平均モデル)
SARIMAモデル(Seasonal Auto Regressive Integrated Moving Average)は、ARIMAモデルにS(季節性) を加えたモデルです。SARIMAモデルは、季節性を考慮するために、季節性の周期に合わせた差分を取ることが必要です。
通常、季節性の周期に合わせた差分を取るためには、データを季節周期に分割し、その差分を取ります。季節周期に合わせた差分を取ったデータに対して、ARMAモデルを適用します。
SARIMAモデルは季節性がある場合に適用するため、季節性のないデータに対してはARIMAモデルが適しています。
2. 状態空間モデルから入る
状態空間モデルは、ほとんどの時系列モデルを表現できる柔軟性の高い時系列分析のモデルです。データの生成過程を「状態」と「観測」から構成される2つの変数の系列としてモデル化し、時間とともに変化する状態に対して、未来の観測値を予測するために用いられます。
3. 機械学習にもっていく
時系列データを部分時系列化したり、高速フーリエ変換を用いて周波数空間に変換するなどして特徴量を作り、それを入力データとした機械学習を行います。時系列データを部分時系列に変換すれば、どの手法でも計算できます。
例として、線形回帰、k近傍法、決定木、ランダムフォレスト、ニューラルネットワークなどが挙げられます。
時系列解析の進め方:7ステップ
時系列解析の進め方について、7つのステップで紹介していきます。
1. 基礎集計
まずは、基礎統計量の算出や欠損の確認、データの可視化などを行います。データの最小値、最大値、平均値、分散、相関係数などの統計量を算出したり、グラフを出してデータの傾向や変動の程度を把握したりします。
2. 前処理
次に、時系列解析を行うための前処理を行います。具体的には以下が挙げられます。
質的変数への対処
欠損への対処
外れ値への対処
スケールが異なるデータへの対処
データ間隔のリサンプル
タイムゾーンの変換
3. トレンドの分析
時系列データは短期的に細かく変動しやすいため、全体の大まかな傾向(トレンド)をつかみにくい場合が多いです。そのため、周辺の値の平均を求めて平滑化します。これを「移動平均」と呼びます。移動平均には「単純移動平均」や「指数平滑移動平均」があり、時系列データによって適切な手法を用います。
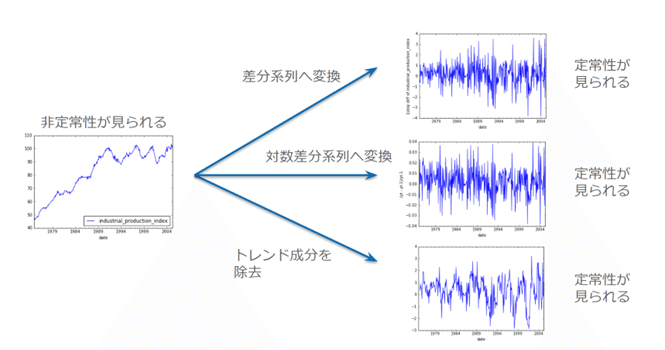
4. 系列の変換
元の時系列データ(原系列)を他の系列に変換します。時系列データには、非定常性や非線形性などの問題が存在する場合があります。これらの問題を解決するために、データを対数系列や対数差分系列へ変換したりします。
5. 周期性の分析
時系列データには、季節性や周期性が存在する場合があります。周期性の分析として、高速フーリエ変換や自己相関係数、偏自己相関係数の算出を行います。
6. 特徴抽出
時系列データには、複数の要素が絡み合っている場合があります。特徴抽出では、これらの要素を分離し、分析に必要な特徴の抽出を行います。
7. モデリング
最後に、時系列モデルを構築します。時系列モデリングとしては第5章で紹介した通り、次の3つのアプローチがあります。
自己回帰系モデルから入る
状態空間モデルから入る
機械学習にもっていく
時系列モデリング手法を選択する際は、解釈性、計算負荷、モデリングの難しさ、モデルの表現力の4つの観点を大事にすることが重要です。
時系列解析で用いられるツール
時系列解析で用いられるツールとして、statsmodelとProphetを紹介します。
statsmodel
statsmodelはpythonの統計解析ライブラリで、時系列解析用APIが充実しています。ARIMAモデルなどの代表的な時系列モデルを扱ったりグラフを描画する機能もあるため、データを視覚的に分析することも可能です。
Prophet
ProphetはFacebookのCore Data Science teamが開発したオープンソースの時系列解析用のライブラリです。PythonやRで利用することができ、こちらもグラフを描画するための機能が充実しています。
Prophetの優れた点として、欠損値があっても問題なく学習ができる点や、予測結果が解釈しやすい点などが挙げられます。Prophetについては、将来予測で用いられるライブラリ「Prophet」で詳しく解説しているのであわせてご確認ください。
時系列解析の事例
時系列解析の事例を3つ紹介します。
事例1. 経済時系列の変動要因分解
1つ目は、実質GDPの変動を解析するために状態空間モデルを使用した事例です。この事例では、以下の3つのモデルが提案されています。
自己回帰成分にトレンド成分を加えた基本モデル
基本モデルに労働力や資本力などで計算される生産関数を確定項として取り込んだモデル
基本モデルと確定項に加えて公定歩合などの経済政策を外因性項として取り込んだモデル
参考文献:時系列解析の実際I(新装版) (統計科学選書),赤池弘次,北川源四郎,朝倉書店,2020
事例2. 人工衛星の姿勢制御
2つ目は、人工衛星データの姿勢を推定する手がかりとして状態空間モデルの手法であるカルマンフィルタを使用した事例です。なお、拡張カルマンフィルタは、アポロ宇宙船を制御するために開発された手法であり、現在でも人工衛星における姿勢制御の基礎技術となっています(参考)。
参考資料:Fundamentals of Spacecraft Attitude Determination and Control,F. Landis Markley 他
事例3. 深層学習を用いた台風強度推定
3つ目は、深層学習を用いて台風の強度を推定した事例です。従来は、衛星が取得した雲画像から得られた台風の雲パターンと台風強度を統計的に関連付けていました。そこで、時系列解析技術として、時間的に連続な画像をCNNに入力し、得られた出力結果を順にLSTMに入力することで台風の中心気圧を予測しました。
参考文献:加瀨紘熙,深層学習を用いた台風強度推定に対する台風の特徴の影響,日本気象学会,66,p51-58,(2019)
時系列解析の課題
時系列解析の実行にあたり、知っておくべき課題もあります。ここでは、下記2つの課題について説明します。
将来予測は必ず的中するわけではない
データの蓄積量が少ないと確度が下がる
将来予測は必ず的中するわけではない
時系列解析を行って得られた将来予測は、必ず的中するわけではありません。そのため、予測が外れるリスクを考慮しておく必要があります。時系列解析以外のさまざまな解析・予測の結果とあわせて考えるべきでしょう。
データの蓄積量が少ないと確度が下がる
データの蓄積量の少ない時系列に対して解析を行うと、分解によって得られた結果が不適切なものとなる場合があります。例えば、直近1週間のデータを用いて年変動の周期変動分析を行った場合、予測結果の確度は大きく下がってしまうでしょう。
時系列解析の学習方法
近年、さまざまなデータが利用されるようになり、今後さらに時系列データの重要性が高まっていくことが予想されます。しかし、いざ時系列解析を使おうとしても、業務の現場でどのモデルを用いて解析して、解析した結果をどのように評価すればよいかといった問題点が出てくるかもしれません。
スキルアップAIでは、時系列データの基礎から時系列モデリングの実装、実践的な分析のノウハウまで身につけることができる「現場で使える時系列解析講座」を提供しています。

本講座は、座学、演習、通し課題で構成されています。座学では、時系列データの前処理から状態空間モデルまで、時系列解析を行うための基礎知識を横断的に学べます。
そして演習では、statsmodels、Prophet、PyStanなどの時系列解析向けのツールについて、実装方法や活用例を学習します。通し課題では、時系列データを用いた一連の分析プロセスを経験することによって、現場で使える実践力を身につけていきます。
時系列解析に関するよくある質問
最後に、時系列解析に関してよくある質問とその回答を紹介します。
Q. 時系列解析とは何ですか?
A. 時系列解析は、時間の経過にともなって変化するデータを分析する統計的手法のことです。時系列データを用いて、過去の傾向やパターンを分析し、未来の動向を予測することができます。
Q. 時系列データの特徴は?
A. 時系列データは、時間に沿って観測されるデータの系列であり、次のような特徴があります。
ノイズ:ノイズとは、分析に必要とされない情報のことです。高周波数成分として観測されることが多いです。
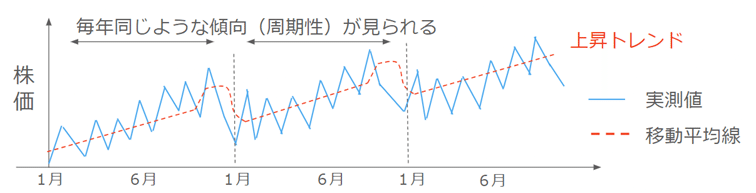
周期性:ある傾向が一定の時間ごとに繰り返されることです。時間によって周期的な変動がある場合があります。
トレンド:時系列データの長期的変動のことです。時間の経過とともに上昇傾向や下降傾向がある場合があります。移動平均を算出することによって、トレンド成分を抽出できることが多いです。
Q. 時系列解析の目的は何ですか?
A. 時系列解析の目的は、時系列データの過去の傾向やパターンを分析し、未来の動向を予測することです。
まとめ
時系列解析は、時間的な変化を調べるための統計手法の一つです。時系列データを分析することで、過去の傾向を把握し、将来の予測を行うことができます。機械学習を応用した手法もあり、精度の高い予測を行うことも可能です。
金融やマーケティングなどの幅広い分野で応用されている時系列解析の需要は高まりつつあります。
時系列解析の知識を深めたい方は、ぜひ本記事を参考にしてみてください。
☆☆☆
スキルアップAIのメールマガジンでは会社のお知らせや講座に関するお得な情報を配信しています。配信を希望される方はこちら
また、SNSでも様々なコンテンツをお届けしています。興味を持った方は是非チェックしてください♪
Twitterはこちら
Facebookはこちら
LinkedInはこちら
スキルアップAI公式YouTube AIビジネスチャンネルはこちら
この記事が気に入ったらサポートをしてみませんか?
