
【理論化学】飽和蒸気圧問題解説
岡山で理系に強い岡山進学研究塾です。今回は理論化学の飽和蒸気圧についての解説です。具体的に簡単な例も出して分かり易く解説していこうと思います。
【お問い合わせ】
086-207-2450
study_support@okashinken.com
【1週間の体験授業・体験学習は公式lineから】

【岡進研HP】



Ⅰ 飽和蒸気圧
高校化学では状態変化を伴う問題を問う場合によく出てくるものです。状態変化に関しての具体例を以下に挙げます。理系知識がない方でもおおまかに理解することは可能かと思います(他分野の話も絡んできますので、完全な理解までは困難かも知れません)。
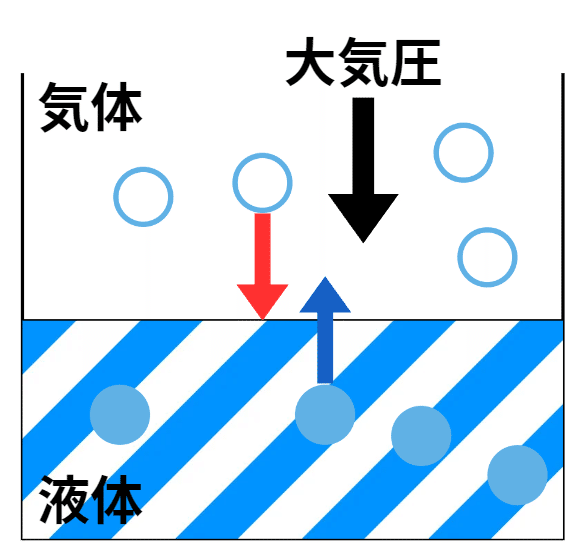
図1に示すように水分子(液体)と水蒸気の分子(気体)が存在するとします。液体→気体が蒸発(気化)、逆は凝縮と言います。実は水の場合、温度が100℃に到達していなくても一部は蒸発(気化)しています。また、凝縮はこの場合、気体分子(水蒸気)が大気による圧力(大気圧)を受けることで生じます(気体分子が大気圧に押されて水面下に潜る、という解釈でも良いかと思います)。飽和という状態は気化する分子数と凝縮する分子数が見かけ上、釣り合ったときの状態を言います(気液平衡)。ここで、
・これ以上圧力を上げるとどうなるでしょうか?
Ⅰ-(ⅰ) 圧力変化による状態変化の推移


圧力を上げると、気体側の分子はより強い力(圧力)を受けることになります。結果、凝縮する方向へ状態変化は進みます。つまり、全体で見ると液体分子(水)の割合が増加します(目で見ると、「水かさが増した」、でもOKです)。逆に圧力を平衡時よりも弱くすると、気化する方向へ状態変化は進みます。
【ポイント】
飽和蒸気圧以上に圧力を上げると凝縮する。
→ ある温度で圧力が飽和蒸気圧以下であれば全て気体と判断することができる(平衡状態時)。・・・(a)
→ 問題を解く際にはいったん状態方程式で圧力を計算して全て気体であるかどうかの確認をする必要があるのはこのためです。
ちなみに、状態方程式は"気体の(もっというなら理想気体限定ですが)"状態方程式ですので、気体分子のみ適用可能です。液体分子の分子数は状態方程式で求めることはできませんので、気化した分子数を計算で求めて、全体の分子数から引いて求める、という形になります。初歩的ですが、共通テストのみならず、2次でもこの基本的な解法で求めるケースが多く存在します。
では、次は温度を上げるとどうなるでしょうか?
Ⅰ-(ⅱ) 温度による状態変化の推移
これは、常識的な知識としてご存じかと思います。容器の温度を上げれば液体は気化する方向へ状態変化は推移します。ちなみに、高校化学の基本ですが、分子どおしは互いに引っ張り合う力(分子間力)が作用しています。しかし、温度を上げると(言い換えれば外部からエネルギーを与えると)、分子間力によって拘束されている分子は実は微振動を起こしていますが、これが活発になり、引力を振り切って自由に動き回れるようになります。拘束力は個体→液体→気体の順に弱くなります。ですので、温度を上げると気化する方向へ状態変化は進みます。


Ⅱ 問題解法時に抑えておきたいポイント
問題は複数のパターンが存在します。以下にてそれぞれの出題に対して抑えておきたいポイントをご紹介いたします。
飽和蒸気圧曲線が出されている場合

(1) 問題文から、27℃でベンゼンは飽和していることが分かります。つまり、ベンゼンの分圧(分圧と全圧はまた機会があればご説明いたします)は1.4×10^4[Pa]と分かります。ベンゼンは全部で0.110[mol]、その内x[mol]が液体で存在しているとすれば、気体の状態方程式より、
(1.4×10^4)×8.3=(0.110-x)×(8.3×10^3)×300
(※気体定数の有効数字も2桁とします)
→ x=6.3×10^4 [mol] ・・・・答え
(2) 77℃でベンゼンが全て気化して気体となっているか、一部は液体で残っているかは不明。したがって、状態方程式に適応させるためには全て気体になっていると仮定するしかない。仮定から求めた圧力値が蒸気圧より小さければ全て気体になっていると判断可能。→Ⅰ-(ⅰ)の(a)
77℃におけるベンゼンの分圧をP1(Pa)とすれば、状態方程式より
P1×8.3=0.110×(8.3×10^3)×350
→ P1≒3.9×10^4[Pa]
この値は77℃におけるベンゼンの蒸気圧よりも小さいため、ベンゼンは全て気化していることが分かります。よって、P1=3.9×10^4[Pa]。アルゴンとベンゼン(気体)の物質量は等しいので、アルゴンの分圧もP1に等しく3.9×10^4[Pa]となります。
アルゴン:3.9×10^4[Pa]
ベンゼン:3.9×10^4[Pa]
・・・・答え
(3) 問題文より、「ベンゼンが全て蒸発(気化)」とあります。そのときの温度をt[℃]、圧力をp(Pa)とすれば、物質量が0.110[mol]、体積は一定(8.3[L])ですので、pとtは直線グラフとなり、蒸気圧曲線との交点を求めれば答えの温度が分かる→グラフ作成系の問題であると判断が付きます。
(※ この手の問題は物理の電磁気学、ダイオードに関する問題でも頻出です)
まずは気体の状態方程式より、
p×8.3=0.110×(8.3×10^4)×(t+273)
(※tは摂氏で定義している)
→ p=110(t+273) ・・・①
①のグラフを正確に書くには、なるべくグラフの温度の両端の値を使用することが望ましいので、t=0[℃]とt=90[℃]の2点と使用します。圧力値は①式へ代入するとそれぞれ3.0×10^4(Pa)、4.0×10^4(Pa)となるので、この2点を結ぶ直線を記すと以下のようになります。

グラフから交点を読み取ると、およそ50[℃]となります。
50[℃]・・・・答え
密閉容器に複数の気体を閉じ込める場合
密閉する、ということは容器内部の分子が容器の外部へ出ることはない、ということです。言い換えれば、状態変化を起こしても総分子数は不変、ということです。それも踏まえて例題を見てみましょう。

(1) 水素1.0g(0.05mol)、酸素32g(0.1mol)だけ存在している。容器内における両者の存在割合(モル分率)はそれぞれ0.05/(0.05+0.1)=1/3
0.1/(0.05+0.1)=2/3となるので、平均分子量をMとすると、
M=2×(1/3)+32×(2/3)=22 ・・・・答え
(2) 水素と酸素を燃焼させて水が生じる反応は
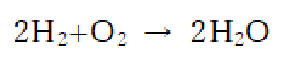
水素0.05[mol]と反応する酸素は0.25[mol]。反応後は水(状態はこの後確認)は0.5[mol]、酸素が1-0.25=0.75[mol]だけ反応せずに残っている。これらを反応前後で簡単な表にまとめる(平衡などでこの表は多用します。即座に表を書く習慣を付けましょう)。

生成した水が全て水蒸気(気体)になったとるす。分圧をP(H2O)とすれば、状態方程式より

この値は、127℃における飽和蒸気圧2.5×10^5[Pa]よりも小さいので、水は全て水蒸気(気体)となっていることが分かるので、分圧は
1.7×10^5[Pa]・・・・答え
(3) 27℃まで冷却すると、水は飽和して凝縮していることから、分圧は問題文より4.0×10^3[Pa]。酸素は0.75[mol]のまま反応せずに残っているので、分圧をP(O2)とすると、

よって全圧は両者の和なので、
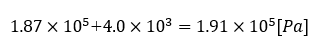
1.9×10^5[Pa] ・・・・答え
まとめ
化学の知識のない方にとっては、途中からは退屈であったかも知れません。しかし、現役受験生にとっては基本的ですが、解答の中で理解していなければならないポイントはこの記事を通じて良い復習になったのではないかと思います。高3生の方は勿論、高2生の方も理科は基礎を終えて発展に入る頃かと思います。岡進研の国立上位校現役合格の一つのポイントは高3進級時までの科目のバランスの取り方にあります。
高1生・高2生の方にも岡進研の個別指導を是非とも体験していただきたいと思います。お問い合わせは下記までお気軽にどうぞ。
【お問い合わせ】
086-207-2450
study_support@okashinken.com
〒700-0023
岡山市北区駅前町1-7-22カタヤマビル5F
岡山進学研究塾
