【Googleのプログラミング面接 あなたは解けるか?】あなたのコンピューターサイエンスの基礎力を試してみよう。
あの有名なHomebrewの開発者、Max HowellがGoogleのコーディングインタビュー受けた時以下の問題に答えられませんでした。
問題
与えられたバイナリツリー(二分木)を反転してください。
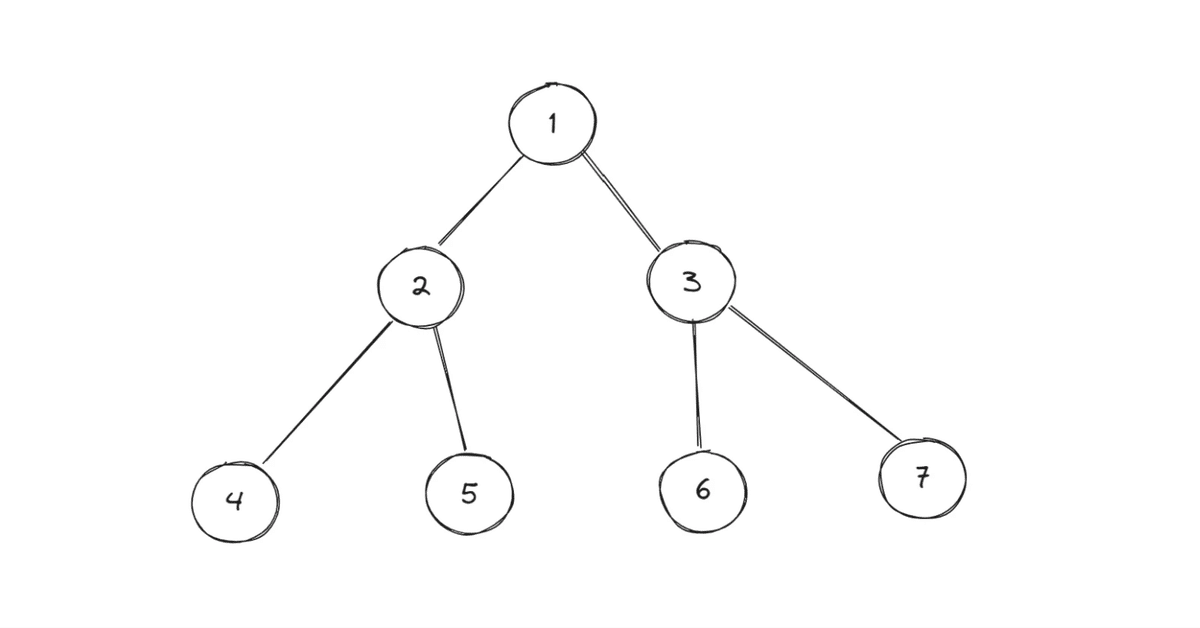
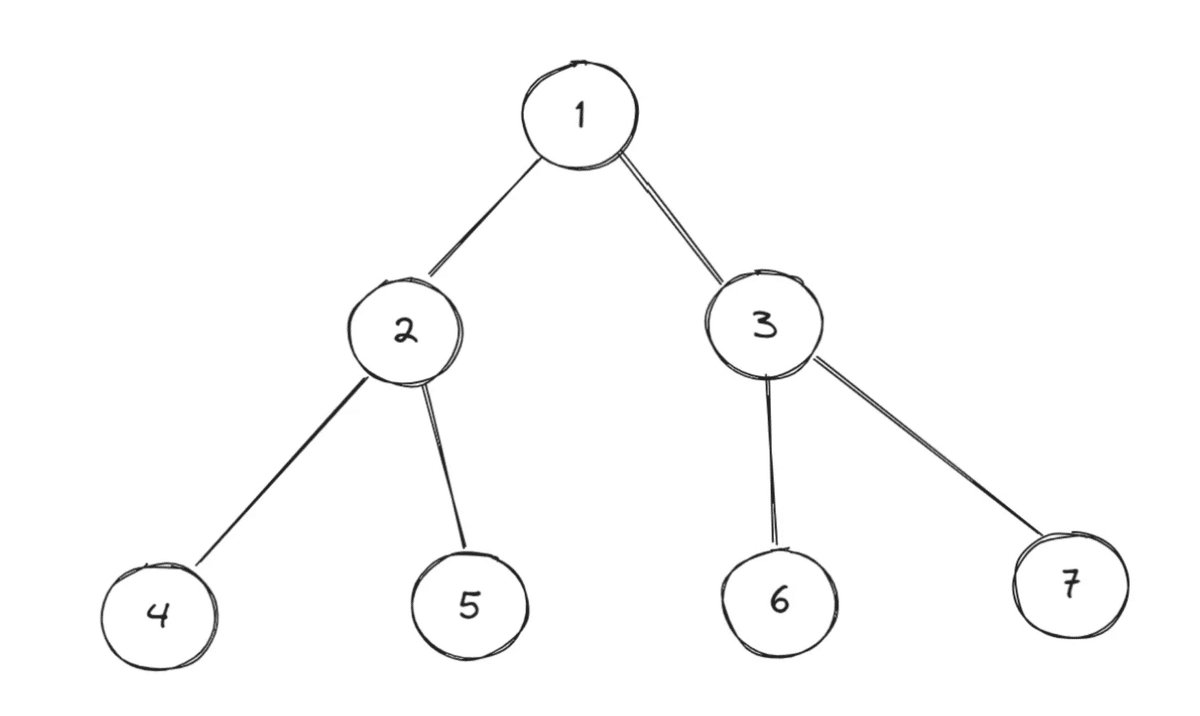
バイナリツリー(二分木)とは?
バイナリツリーは、各ノードが最大2つの子ノードを持つ木構造のデータ構造です。
class BinaryTree:
def __init__(self, value):
self.key = value
self.left_child = None
self.right_child = None
def add_left_child(self, value):
if self.left_child is None:
self.left_child = BinaryTree(value)
else:
self.left_child.add_left_child(value)
def add_right_child(self, value):
if self.right_child is None:
self.right_child = BinaryTree(value)
else:
self.right_child.add_right_child(value)binary_tree = BinaryTree(1)
binary_tree.add_left_child(2)
binary_tree.add_right_child(3)
binary_tree.left_child.add_left_child(4)
binary_tree.left_child.add_right_child(5)
binary_tree.right_child.add_left_child(6)
binary_tree.right_child.add_right_child(7)バイナリツリーの反転とは?
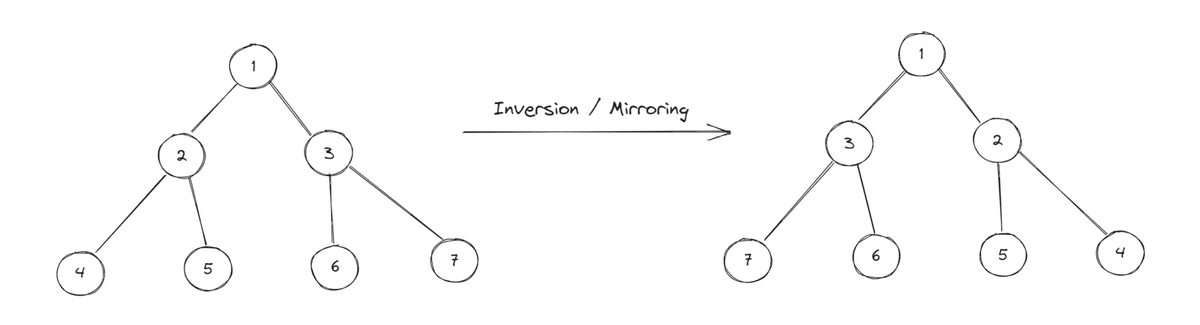
バイナリツリーの反転は、それの左右の子ノードを交換する操作です。 これはミラーリングとも呼ばれます。
幅優先探索アプローチ
バイナリツリーに対して、各レベルごとに幅優先探索で、各レベルの各ノードの左右の子ノードを交換します。 これにより、元のツリーを反転したバイナリツリーが得られます。
def invert_bfs(self):
current_level = [self]
next_level = []
while current_level:
for node in current_level:
if node.left_child:
next_level.append(node.left_child)
if node.right_child:
next_level.append(node.right_child)
node.left_child, node.right_child = node.right_child, node.left_child
current_level = next_level
next_level = []current_levelとnext_levelの2つの配列を使用して、ツリーの次のレベルのノードを配列に追加していきます。 current_levelのすべてのノードを訪れ、next_levelで各ノードの子ノードを追加してから、交換します。 以後、繰り返しで、葉ノードに達するまでやります。
深さ優先探索アプローチ
このアプローチでは、各ノードの左右の部分ツリーを反転させるために、再帰的な深さ優先探索で行います。
def invert_dfs(self):
if self is None:
return None
if self.left_child:
self.left_child.invert_dfs()
if self.right_child:
self.right_child.invert_dfs()
self.left_child, self.right_child = self.right_child, self.left_child完成版
import matplotlib.pyplot as plt
class BinaryTree:
def __init__(self, value):
self.key = value
self.left_child = None
self.right_child = None
def add_left_child(self, value):
if self.left_child is None:
self.left_child = BinaryTree(value)
else:
self.left_child.add_left_child(value)
def add_right_child(self, value):
if self.right_child is None:
self.right_child = BinaryTree(value)
else:
self.right_child.add_right_child(value)
def invert_bfs(self):
current_level = [self]
next_level = []
while current_level:
for node in current_level:
if node.left_child:
next_level.append(node.left_child)
if node.right_child:
next_level.append(node.right_child)
node.left_child, node.right_child = node.right_child, node.left_child
current_level = next_level
next_level = []
def invert_dfs(self):
if self is None:
return None
if self.left_child:
self.left_child.invert_dfs()
if self.right_child:
self.right_child.invert_dfs()
self.left_child, self.right_child = self.right_child, self.left_child
def visualize(self):
fig, ax = plt.subplots(figsize=(8, 6))
self._plot_tree(ax, 0, 0, 100)
ax.set_aspect('equal')
ax.axis('off')
plt.show()
def _plot_tree(self, ax, x, y, dx):
if self is not None:
circle = plt.Circle((x, y), radius=5, color='b', fill=True)
ax.add_patch(circle)
ax.text(x, y, str(self.key), va='center', ha='center', color='w', fontsize=12)
if self.left_child:
dx_new = dx / 2
x_left = x - dx_new
y_left = y - 50
ax.plot([x, x_left], [y, y_left], color='k')
self.left_child._plot_tree(ax, x_left, y_left, dx_new)
if self.right_child:
dx_new = dx / 2
x_right = x + dx_new
y_right = y - 50
ax.plot([x, x_right], [y, y_right], color='k')
self.right_child._plot_tree(ax, x_right, y_right, dx_new)# Example usage:
binary_tree = BinaryTree(1)
binary_tree.add_left_child(2)
binary_tree.add_right_child(3)
binary_tree.left_child.add_left_child(4)
binary_tree.left_child.add_right_child(5)
binary_tree.right_child.add_left_child(6)
binary_tree.right_child.add_right_child(7)print("Original Tree:")
binary_tree.visualize()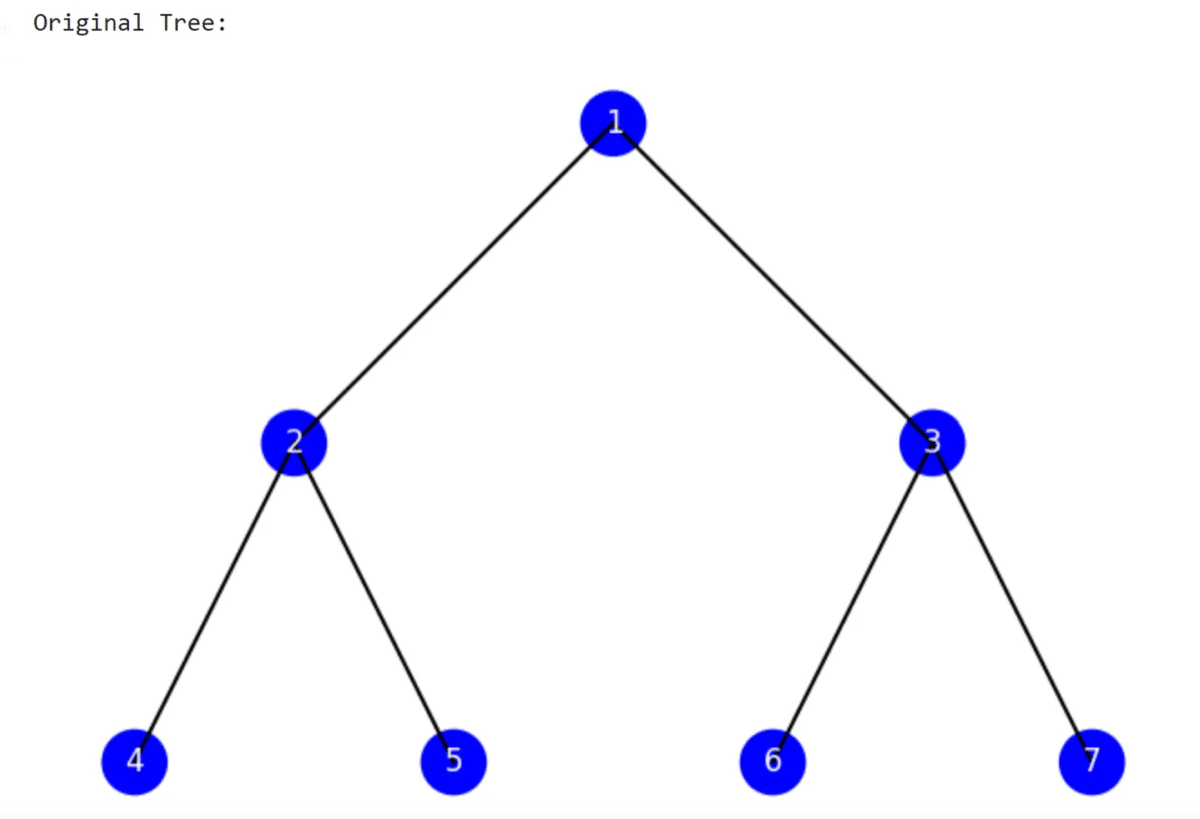
# Invert the binary tree
binary_tree.invert_dfs()
print("\nInverted Tree:")
binary_tree.visualize()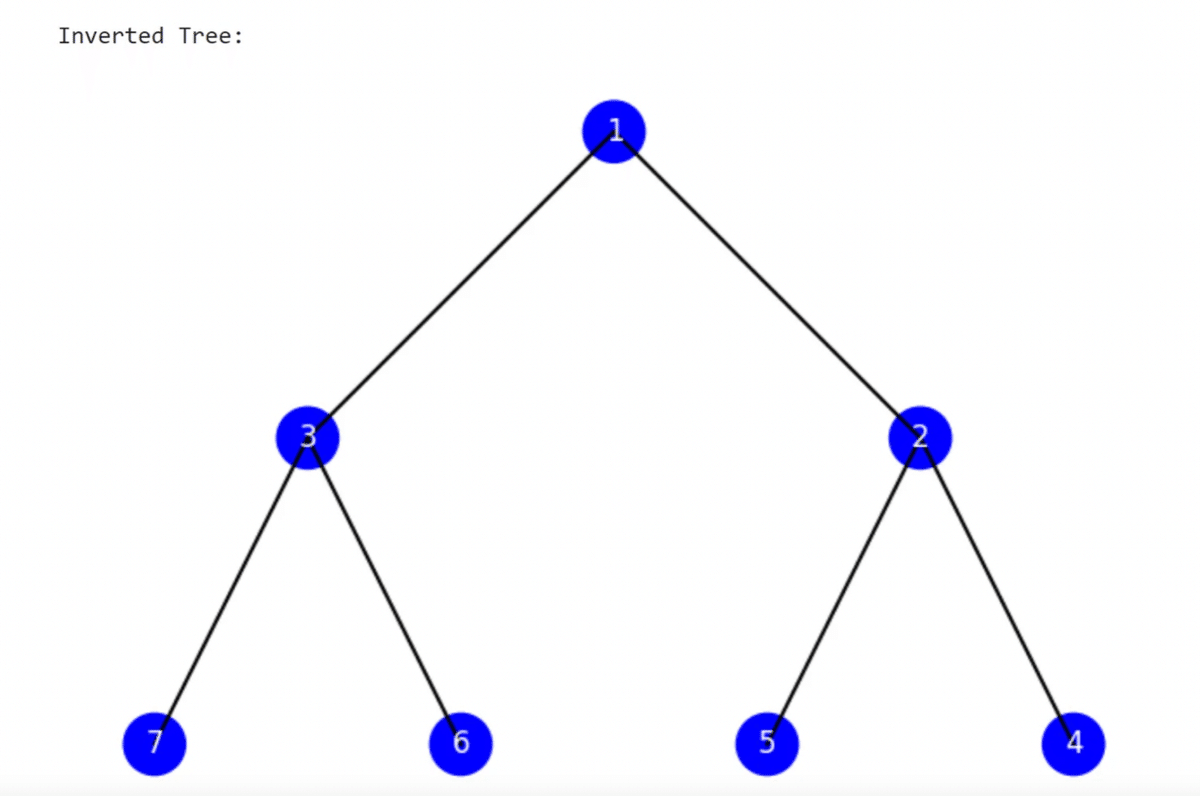
実際にやってみると、1つの基本的なデータ構造と2つの基本的な探索アルゴリズムを理解できるているかを問われる問題ですね。面接を通して、どれだけ基本を理解しているかを重視しているかがわかります。
