【実例で学ぶ】Pythonで実装する最もシンプルなダイクストラ法
ダイクストラ法とは?
ダイクストラ法は、エドガー・ダイクストラが発明した、グラフ上で最短経路を見つけるためのアルゴリズムです。ここでいうグラフは、地図やネットワークなど、点と点が線でつながっている構造のことを指します。
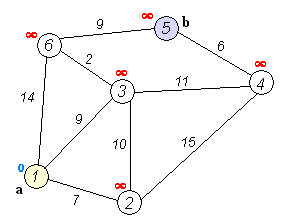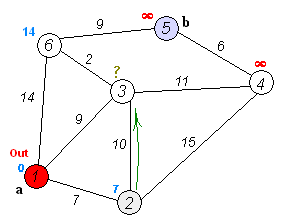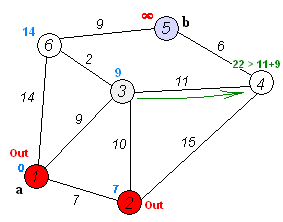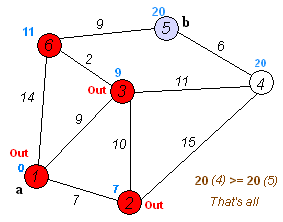
このアルゴリズムは、「重み付きグラフ」(各エッジが一定のコストや距離を持つグラフ)における最短経路問題を解くのに適しています。
ダイクストラ法は、以下のように動作します:
アルゴリズムは、スタートノードから始めます。
そのノードから直接結びついているノード(隣接ノード)への距離を計算します。すでに計算済みの距離がある場合、より小さい値のもので更新します。
スタートノードからの最短距離が確定したノードを「確定ノード」とします。スタートノードから最短の距離が未確定のノードを「未確定ノード」とします。
すべての未確定ノードの中から最短距離のノードを選び、そのノードから直接結びついている未確定ノードへの距離を計算し、更新します。
ステップ4を全てのノードが確定ノードになるまで繰り返します。
Pythonでのダイクストラ法の実装
以下は、Pythonを用いたダイクストラ法の基本的な実装例です。
import heapq
def dijkstra(graph, start, end):
distances = {node: float('infinity') for node in graph}
distances[start] = 0
queue = [(0, start)]
while queue:
current_distance, current_node = heapq.heappop(queue)
if current_node == end:
return distances[end]
if distances[current_node] < current_distance:
continue
for neighbor, weight in graph[current_node].items():
distance = current_distance + weight
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(queue, (distance, neighbor))
return None
# グラフの定義
graph = {
'A': {'B': 1, 'C': 4},
'B': {'A': 1, 'C': 2, 'D': 5},
'C': {'A': 4, 'B': 2, 'D': 1},
'D': {'B': 5, 'C': 1}
}
print(dijkstra(graph, 'A', 'D')) # Output: 4
ダイクストラ法は、様々な現実の問題に対して使用することができます。最も一般的な応用例は次のとおりです:
GPSナビゲーション: GPSナビゲーションシステムは、2つの地点間の最短経路を計算するためにダイクストラ法を用いています。それぞれの地点(交差点や目的地など)はノードとして、道路はエッジとして表現され、エッジの重みは距離や時間などで表されます。
ネットワークルーティング: パケットを送信元から送信先へと効率的に転送するために、ネットワークルーティングアルゴリズムはダイクストラ法を用いて最短経路を計算します。
ソーシャルネットワーキング: あるユーザーから別のユーザーへの最短経路(つまり、最小数の中間フレンドを通じて)を見つけるために、ソーシャルネットワーキングサービスはダイクストラ法を使用することがあります。
以下に、Pythonでのダイクストラ法を用いたGPSナビゲーションシミュレーションの簡単な例を示します:
import heapq
def dijkstra(graph, start, end):
distances = {node: float('infinity') for node in graph}
distances[start] = 0
previous_nodes = {node: None for node in graph}
queue = [(0, start)]
while queue:
current_distance, current_node = heapq.heappop(queue)
if distances[current_node] < current_distance:
continue
for neighbor, weight in graph[current_node].items():
distance = current_distance + weight
if distance < distances[neighbor]:
distances[neighbor] = distance
previous_nodes[neighbor] = current_node
heapq.heappush(queue, (distance, neighbor))
path = []
while end:
path.append(end)
end = previous_nodes[end]
path.reverse() # Reverse to get path from start to end
return distances, path
# 都市間の道路ネットワーク(都市がノード、道路がエッジ、道路の長さが重み)
graph = {
'Tokyo': {'Osaka': 500, 'Nagoya': 350},
'Osaka': {'Tokyo': 500, 'Nagoya': 150, 'Fukuoka': 600},
'Nagoya': {'Tokyo': 350, 'Osaka': 150},
'Fukuoka': {'Osaka': 600}
}
# 東京から福岡までの最短距離と経路を計算
distances, path = dijkstra(graph, 'Tokyo', 'Fukuoka')
print("最短距離: ", distances['Fukuoka']) # Output: 最短距離: 1100
print("最短経路: ", " → ".join(path)) # Output: 最短経路: Tokyo → Nagoya → Osaka → Fukuokaこのコードでは、都市間の道路ネットワークを表現したgraphから、東京から福岡までの最短距離をダイクストラ法を用いて計算します。実際の道路ネットワークでは、双方向の道路や交通量、交通規制、道路の状態なども考慮に入れる必要があります。
