
ロジスティック回帰をscikit-learnを使わずゼロから実装する(Python)
機械学習を理解するにはアルゴリズムをから実装するのが一番です。そして問いデータを使って遊んでみましょう。
ロジスティック回帰とは、二項分類(2値分類)を行うための方法です。二項分類とは、ある物体がAかBのどちらかに分類することを指します。例えば、試験の点数が60点以上かどうかで分類することができます。
ロジスティック回帰では、試験の点数だけでなく、その他の情報も考慮に入れることができます。例えば、試験の点数だけでなく、勉強時間や家庭環境なども考慮に入れることができます。これらの情報を使って、試験の点数が60点以上かどうかを推定することができます。
import numpy as np
class LogisticRegression:
def __init__(self):
self.w = None
self.b = None
def fit(self, X, y, learning_rate=0.001, num_iter=100000):
num_samples, num_features = X.shape
# 重みとバイアス項を初期化
self.w = np.zeros(num_features)
self.b = 0
# 勾配降下法
for i in range(num_iter):
# テストデータと重みとバイアスを計算
output = self.sigmoid(np.dot(X, self.w) + self.b)
# 正解と予測の誤差を計算
error = y - output
# 重みとバイアス項を更新
self.w += learning_rate * np.dot(error, X)
self.b += learning_rate * error.sum()
if(i % 1000 == 0):
print(f'loss: {self.loss(output,y)} \t')
# シグモイド関数
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
# 損失関数
def loss(self, h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
def predict(self, X):
# テストデータの予測値を計算
output = self.sigmoid(np.dot(X, self.w) + self.b)
# 予測値を返却
return (output > 0.5).astype(int)
# 学習データ
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.array([0, 0, 1, 1])
# テストデータ
X_test = np.array([[5, 6], [6, 7]])
y_test = np.array([1, 1])
# インスタンス化
model = LogisticRegression()
# データをモデルにfit
model.fit(X, y)
# テストデータで予測
predictions = model.predict(X_test)
# 結果
print(predictions)
[1 1]
シグモイド関数とは、非線形の関数の1つであり、活性化関数としてよく使われます。シグモイド関数は、以下の式で表されます。
S(x) = 1 / (1 + e^(-x))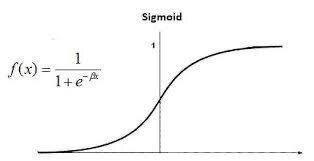
特定の入力値から、0から1までの値を出力する関数です。例えば、入力値が0の場合には0.5が出力され、入力値が大きくなるにつれて、出力値は1に近づいていきます。逆に、入力値が負の場合には、出力値は0に近づいていきます。
シグモイド関数は、0から1までの値を出力するため、入力値が0から1までの値をとるような問題に特に適しています。例えば、試験の点数が0から100までの値をとる場合、シグモイド関数を使うことで、試験の点数が60点以上かどうかを推定することができます。
ロジスティック回帰のloss function(損失関数)は、以下の式で表されます。
L(y, p) = - (y * log(p) + (1 - y) * log(1 - p))ここで、yは正解ラベル、pはモデルが予測する確率、L(y, p)はloss functionの値を表します。コードは以下の部分ですね。
def loss(self, h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()ロジスティック回帰のloss functionは、値が小さいほどモデルが正解ラベルを正しく予測していることを意味します。したがって、ロジスティック回帰では、loss functionの値を最小化するような重みとバイアスを求めることで、モデルの性能を最大化することができます。
loss functionはそのまま使うのではなく、偏微分して以下の形にします。勾配降下法の中で使います。
self.w += learning_rate * np.dot(error, X)
self.b += learning_rate * error.sum()以下、機械学習のオススメ書籍。この順番で学ぶと理解が深まります。
