
イメージで理解できる-ゼロ知識証明
暗号通貨でもよく取り上げられる、ゼロ知識証明について、以下の記事が分かりやすかったので、みなさんにも紹介したいと思います。
数式は一切登場しません。イメージで理解でます。
引用元
ゼロ知識証明って??
ゼロ知識証明とは、ある人(証明者)が別のある人(承認者)に対して、与えられた情報が「真実である」ということ以外の情報を相手に与えずに、その情報が実際に「真実」であることを証明する手法のことです。
暗号学で使われている、証明プロトコルの一種なんですが、これだとまだ理解できないですね。
証明とは、ある主張が正しいこと納得させる手段です。そして、証明プロトコルとは主張を納得させたい証明者と、証明の正しさを確かめる検証者が存在し、最終的に検証者を納得させる暗号プロトコルです。※プロトコル:処理手順
具体的に、どういう時に使うのでしょうか?
・Webサービスにログインする時:パワードを入力する代わりに、パスワードを知っているという証拠を送る。
・本人確認する時:第三者に母親の旧姓を送る代わりに、自分が確実に本人であることの証拠を送る。(デジタル署名)
・ブロックチェーンにトランザクションを送る時:パブリックブロックチェーンに、トランザクションを送るとの違って、自分の過去のトランザクションを明かすことなく、二重払いしていないことの証拠を送る。(ZCash)
つまり、相手に秘密を直接伝えず、秘密を知っていることを証明する方法です。
パスワードを与えずに、パスワード知っていることを相手に証明する?なんだか難しそうですね。一体どうやって行うのでしょうか?引用元のブログ記事を参考に、具体的なプロセスを見ていきましょう。
例1:「ウォーリーをさがせ!」で、あなたがウォーリー見つけたことを、位置情報を示すことなく証明せよ。
この例では、アリスとボブが「ウォーリーをさがせ!」という絵本で、ウォーリーを見つけるために競い合います。

右の絵の中から彼を探せ。
謎々
アリス:ウォーリーを見つけたわ!
ボブ:嘘つきって、どういう意味だがわかるよね?
アリス:彼の正確な場所を教えることなく、見つけたことを証明できるわ。
アリスは間違っていないとことを証明するため、2つの方法を考え出しました。
証明1
アリスは絵から、ウォーリーだけを切り抜いて、ボブに見せます。念のため、アリスが単にウォーリーの絵を、新しくコピーしただけでないことを証明するには、絵全体の裏面に透かしを入れておきます。

証明2
アリスはオリジナルの絵全体に、カードボードを被せて、ウォーリーの箇所だけ切り抜きます。こうするとウォーリーだけが見えます。彼の位置情報はボブには一切開示していません。アリスはカードボードを、絵に被せるだけでいつでも、ウォーリーを見つけたことを証明できます。

健全性、完全性、そしてゼロ知識
どちらの証明方法も、ゼロ知識証明を構成する3つの要素を満たしています。
アリスは毎回同じゲームを行ったとしても、同じ方法でウォーリーを見つけたことを証明できます。
1.健全性- 証明できることは全て真でなければならない:アリスが、ウォーリーの場所を知らないとして、カードボードをランダムに切り抜いたとしましょう。カードボードの穴は、ウォーリー以外のランダムなイメージを表示するだけです。要するに、アリスの証明システムでは、ズルすることはできません。
2.完全性-真であるには証拠がなければならない:アリスは、ウォーリーを探すたびに、毎回ボブに同じ方法で証明することができる。アリスの証明システムで、ボブにウォーリーを見つけたことを毎回納得させられる。
3. ゼロ知識- 証明されたという事実だけが表明される:アリスが、ボブにウォーリーを見つけことを証明するには、ボブに対して「アリスがウォーリーを見つけた」以外の情報は提示されない。ウォーリーの正確な位置情報は、提示されることはありません。アリスは、自身の情報を一切開示することなく、ウォーリーを見つけたことを証明できます。
例2: 対話証明-ゼロ知識証明
続いては、対話証明(二人が通信する)ゼロ知識証明の例です。この例ではアリスは色盲で、ボブは色を識別できると仮定します。ところが、アリスはボブに色が見えるということが信じられません。
賢い暗号学者であるアリスは、2つのボール(赤と青)を使った方法でボブには色が見えることを証明します。
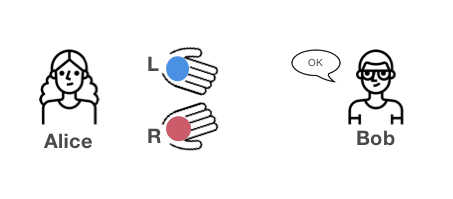
アリス:私は今、赤と青のボールを持っています。ボールを持ったまま、両手を後ろに隠します。その時に、ボールを入れ替えるかもしれません。入れ替えないかもしれません。どちらにしろ、ボールは再度ボブに見せます。
ボブ:了解。つまり、ボールを入れ替えたかどうか、教えて欲しいと言うことだね。
アリス:その通り。色が見える人だけが、私が交換したか、常に当てることができるわ。
アリス:さて私は、ボールを入れ替えたでしょうか?
ボブ:入れ替えた。ボールはさっきと違う手にある。
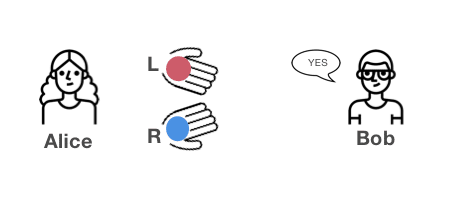
アリス:私はボールを入れ替えたでしょうか?
ボブ:入れ替えてない。ボールはさっきと同じ手にある。
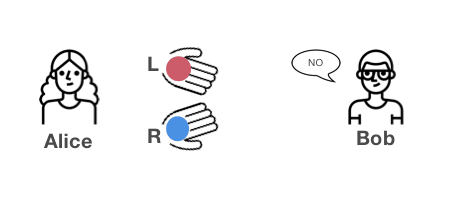
この証明では、アリスが納得するまで何度も繰り返します。20回もゲームを繰り返すと、ボブが偶然正解を当てる確率は、1,048,576/1回であることがわかります。ボブには色が見えていることを、アリスは納得できました。(ボブはボールの色情報を伝えることなく、色が違うことをアリスに納得させました。)
- もしボールが同じ色だとしたら、ボブはランダムに当てることになり、確率は劇的に下がります。
対話証明-ゼロ知識証明での正しさは、統計上的に保証するだけです。
例3: 非対話証明-ゼロ知識証明
続いては、非対話証明(お互いが通信しない)ゼロ知識証明の例です。アリスとボブの間いに、やり取りは発生しません。この例ではアリスは証明できたことの証拠を事前に作り上げます。ボブは事後確認します。この非対話型の方法は、ボブのみならず、不特定の誰でもアリスの証明を確認できます。
謎々
アリスは誰も解けなかった、数独パズルを解いたこと証明したいとします。

数独:行、列、3x3マス、全て1-9のみの数字で構成しなければなりません。
アリスは、不正できないシステムを組み上げたとして、ボブと仲間に証明できとこと提示します。アリスのシステムは誰が見ても明確です。誰でも確認できるプロトコルで証明します。
1.最初にアリスは、まだ解けていないパズルを生成し、すでに判明している数字の上に、同じ数字の3枚のカードを置きます。例:C3のセルは9のカードが3枚になります。

2.次にアリスは、答えを伏せたカードで、同じように3枚ずつ置いておきます。(今回は伏せます)。ボブは、まだこの時点でカードを見てはいけません。
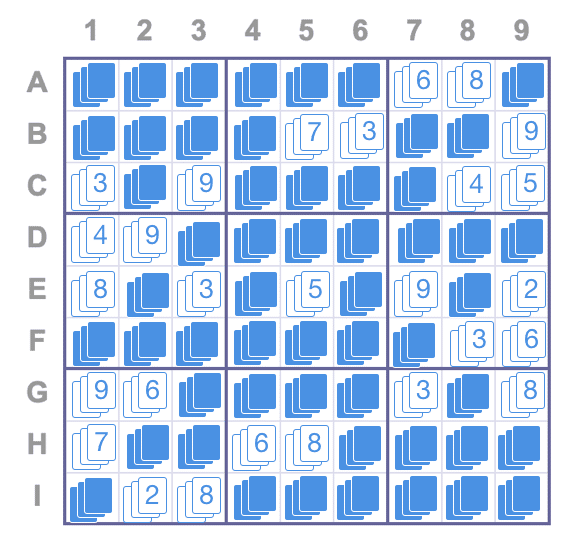
3.ここからカードの内容を確認する手順です。まず行から初めて、列、3x3のマスのカードを確認していきます。
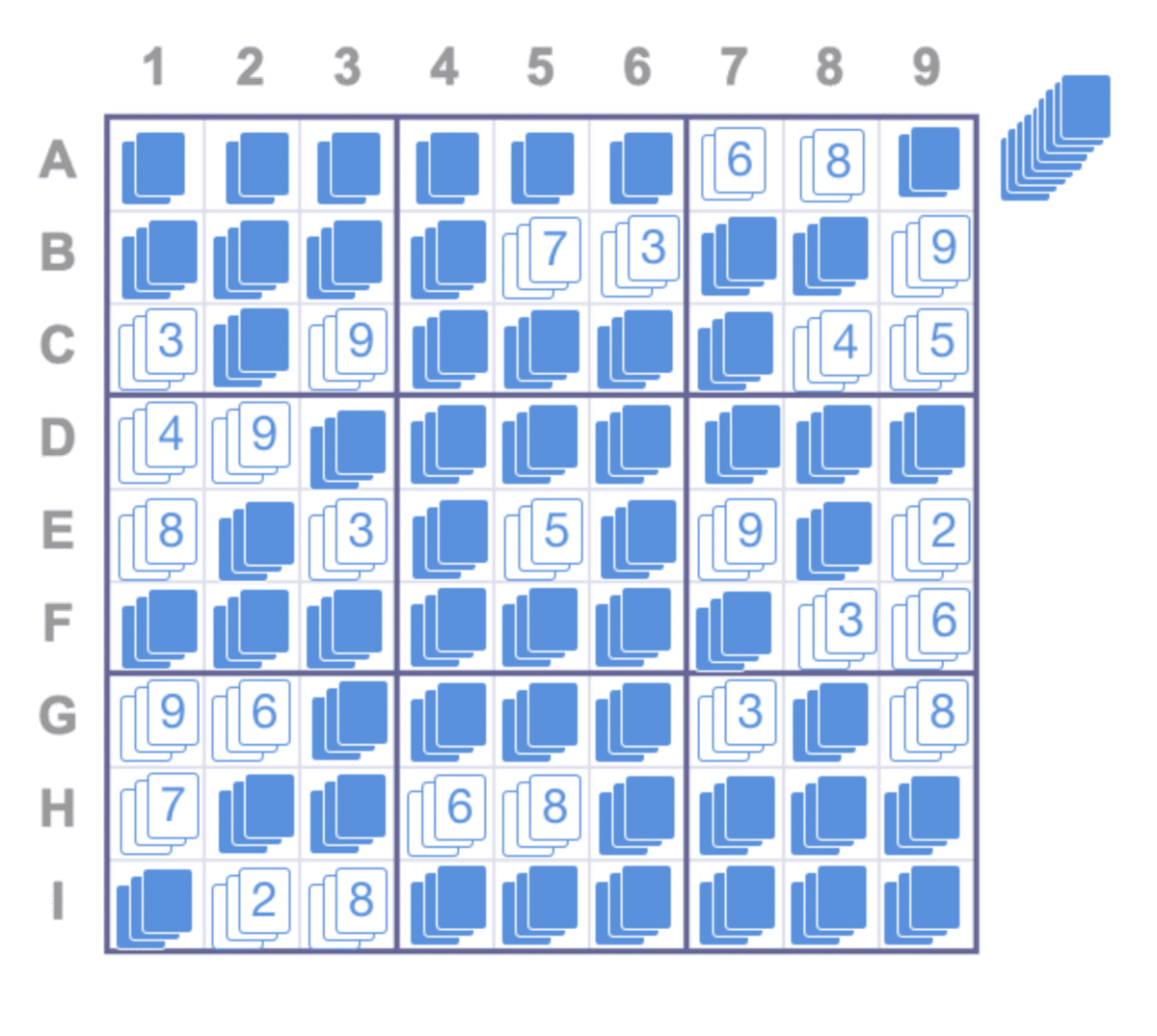
行1のカードだけ集めます。
手順は、9枚のカードの束を伏せたまま、集めていきます。これを行、列、3x3のマスごとに繰り返していくと、27束が出来上がります。
行9束+列9束+3x3のマス9束 = 27束
4.各束をシャフルしてボブに渡していきます。
5.ボブはカードを裏返して、1~9の数字が漏れなくダブなくあるか、確認していきます。

シャフルされたカードなので、すでに初期順には並んでいません。
確認作業のあと、ボブとその仲間たちは、アリスが確かに数独パズルを解いたことを確認しました。
わからない人へ→27束全て1−9の数字のみで構成されていれば、解いたことになります。
非対話証明の例では、アリスが証明したということを、システム(コード)を使って誰もが確認できます(手順が明確なので)。直接アリスに問い合わせずとも、証明の結果だけで確認することができます。
どうですか?かなりイメージできたと思います。面白かったらぜひシェアしてください!
暗号はインターネットと暗号通貨を保証しているものですね。ビットコインも暗号という文脈から、誕生しました。
