今日は子どもの日

今日は子どもの日です。

総務省の統計によると、15歳未満の子どもの数は、2020年よりも19万人少ない1493万人で、40年連続の減少だそうです。

総人口に占める子どもの割合は、11．9％で、こちらは47年連続減少。

そんな少子化にもかかわらず、都市部を中心に中学受験熱は

上がる一方です。

コロナ禍で貧困が叫ばれる中、私立中を目指す人が増えるのは

何か皮肉なものを感じます。

そんな中学受験にも大きな変化の波が来ています。

かつては、受験といえば、暗記、というイメージありましたが

これが、大きく変わろうとしています。

それが、大学入試改革に伴う、「思考力・判断力・表現力」重視です。

元々中学入試では、難関校ほど単なる暗記では解けない問題が

出題される傾向にありました。

例えば、昨年度の浦和明の星女子中学校の算数で、こんな問題が出題されました。

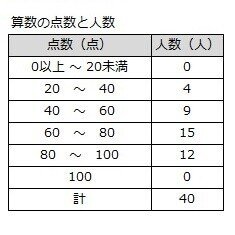
表から読み取れることとして、必ず正しいといえるものには○
そうでないものには×を書き入れよ。

問い「算数の平均点は、60点以上である」

さあどうでしょうか？

平均点の出し方は分かっても、度数分布からは難しいですね。

しかも、「必ず」とあるのも曲者です。

表を見ると60点以上が27人もいます。

全員で40人なので、平均点としては絶対に60点以上

となる

ような気がしますよね。

しかし、最悪？のことを考えてみましょう。

つまり、

20点～40点の分布を全員20点

40点～60点の分布を全員40点

60点～80点の分布を全員60点

80点～100点の分布を全員80点

と考えてみたらどうなるでしょうか？

20×4＋40×9＋60×15＋80×12=2300

つまり、素点合計が2300点になります。

なので、40人の平均点は

2300/40=57.5

57.5点となります。

どうですか？

この条件であれば、平均点が60点を下回るんですね。

まあ、こんな条件は普通はありえない、と思いますが、条件が「絶対」なので、答え的には「×」になる訳です。

感覚的な答えと、あり得ない答えが、最悪の条件の答えでは、こんなにも差が出る訳です。

ここら辺が、「思考」を伴う設問、ということになります。

じゃあ、こんな思考を深めるには、どんなことをすればいいのか？

ここら辺は、難しい課題ですが、ざっくりいうと、国語力の向上だと思います。

具体的な方法については、「22時就寝でも合格した勉強法」の一般販売でお伝えしていく予定です。