針ゲにおける技術解説
まず初めに
この記事は針ゲに関する技術、知識をまとめたものです。
中国のMr.Chen233による針ゲ記事「Needle Techniques」を元に、理解し安いよう説明、画像等を追加しました。また、元記事内の幾つかの画像を引用しています。
また、一部解説でnameless様のお力添えを頂きました。
一部の情報は私が要らないと判断した箇所があります。また、元記事にない項目の追加も行いました。
複数の翻訳サイトを使用したり、事実との関係をしっかりと確認しながら書いていますが、正確な翻訳が一部できていない可能性があるため、間違った情報を提供している場合があります。お気づきの際は X か Discord に一報いただけると幸いです。
情報が不足している部分があり、憶測で説明している箇所があるので、その部分には取り消し線が引いてあります。
プレイヤーのコードに基づく基本的な動き
まず、Gamemakerに関する用語を理解することから始めましょう。
フレーム
静止した画面のこと。
フレームレート
1秒間のフレーム数。fps。
スピード
1フレーム内のオブジェクトの移動距離。 オブジェクトのスピードが3なら、毎フレーム3ピクセルずつ移動します。
垂直方向と水平方向の速度
垂直方向の速度とは、オブジェクトが上下に移動する速度のことで、水平方向の速度とは、オブジェクトが左右に移動する速度のこと。
重力
1フレームあたりの垂直方向の速度の減少量を指します。(垂直方向に限ったものではないですが、これで十分だと思います。)
例えば、重力が0.4だった場合、垂直方向の速度は毎フレーム0.4ずつ減少します。
アイワナにおける上記を踏まえた基本事項
フレームレート: 50
プレイヤーに関する情報
プレイヤーの歩くスピード 3
プレイヤーの重力 0.4
1段目ジャンプのコード上の初速度 8.5(重力加算により、8.1になります)
2段目ジャンプのコード上の初速度 7(重力加算により、6.6になります)
プレイヤーのコード上の最大落下速度 9(重力加算により、9.4になります)
Shiftキーを解除した場合の垂直方向の減速度 0.45倍
プレイヤーがジャンプをするに当たり使用するキーをShiftキーとします。
また、ここで出てくる数値は今後の説明で多用しますので、何の数値か覚えておくと良いです。
技術を解説するに当たっての表記説明
以下は解説をするに当たって、必要な表記に関しての説明をしています。
(m+n), (m+n+o)…
Shiftキーを押下してから解除するまでのフレーム数。
例: (2+5)であればShiftキーを押下してから、2フレーム後と7フレーム後にShiftキーを解除することになります。
基本的に(1+n)、(1+n+o)…はジャンプキャンセル、それ以外はカクタスと呼ばれます。これに従うと、上記例のジャンプは「(2+5)カクタス」ですね。
V-String
日本ではよく縦ドットと呼ばれることが多いですが、小数点以下の縦ドットと混同されるので、この記事内では「V-String」と表記します。
「V-String」とは技術ではなく、y-positions(ある瞬間におけるプレイヤーの位置)の連続であるプレイヤーの運動軌跡を表現するための用語です。
V-Stringを活用することにより、ある瞬間のプレイヤーの位置と速度を得るだけで、その後のプレイヤーの状態を知ることができます。
したがって、V-Stringは、プレイヤーの位置と速度の両方の変数を同時に記述するために使われる用語であるとも考えられます。
…と言ってもよく分かりませんよね。
V-Stringに関連している例を提示しましょう。

この配置はジャンプをせずに押しっぱなしで降りれる配置として有名ですよね。なぜ押しっぱなしで行けるのか、コマ送りで見てみましょう。

これは、垂直方向の速度がうまく噛み合っていることで可能になっています。1フレームあたりの速度が速くなっているので、ブロックに張り付き終わった後プレイヤーが一歩動いても既に針に当たらない場所にいます。

3マスの場合では更にスピードが付いていますが、ブロックの上のほうで張り付きが終わり、針に当たってしまいます。これは、最初に特定の高さのジャンプなどを入れてV-Stringを変えることによって回避することができます。
このように、配置に対して有利なV-Stringを取得するために行う動作の一連を、「V-Stringを合わせる」、「縦を合わせる」などと表現したりします。
では、技術の解説を始めていきます。
第1章. 横ドット(ドット)、ドット調整
この用語に関しては知っている方が殆どでしょう。
ご存じでない方のために簡単に説明すると、プレイヤーが壁に貼りつくことによって、1ピクセルか2ピクセル分移動できるものです。
針に近づきたい場合や、ブロックの先端に立ちたい場合などに役立ちます。
まだご存じでない方は、こちらの記事が役に立つはずです。
第2章. ジャンプキャンセル
「ジャンキャン」と略称して使われることが多いです。
一般的に、1フレームジャンプ(16ピクセル)以下のジャンプはジャンプキャンセルと呼ばれます。
この用語に関しても知っている方が殆どでしょうが、その原理を説明したものは少ないはずです。
ご存じでない方のために簡単に説明すると、かなり小さなジャンプを出すことができる技術です。

まずここで使用する用語について説明します。
keyboard_check_pressed: キーが押された検出
keyboard_check_released: キーが離された検出
ジャンプキャンセルの原理
基本的に、プレイヤーのジャンプの解除は一度だけ行われます。
ジャンプを弱める為には、Shiftキーを離す必要があり、それには前にShiftキーを押している必要もあります。
ジャンプキャンセルの原理は、1フレームのジャンプの中で何度もShiftキーを解除させ、0.45倍のスピードを繰り返すことで低いジャンプを出すことが可能になるというものです。
しかし、Shiftキーを押している必要があるという前提がある以上、もう一度Shiftキーの解除を試みようとしてシフトを押すと、もう一度ジャンプが出てしまいます。
ではどのようにしてそのような問題を解決すれば良いのでしょうか?
それは、Shiftキーを二つ以上使うということです。
以下がその方法、原理になります。
1つ目のShiftキーはジャンプキャンセルのために押下状態にあるものとします。
1つ目のShiftキーを離すと同時に別のシフトを押すと、Shiftキーのkeyboard_check_pressedイベントとkeyboard_check_releasedイベントが同時に発動します。
コードはShiftキーの解除を検出する前に押下を検出するので、Shiftキーの押下に対応するイベントが最初に発動します。
プレイヤーの垂直方向のスピードを8.5にし、次にShiftキーの解除に対応するイベントが発動して、プレイヤーの垂直方向のスピードを0.45倍にします。
以上が最初のフレームで起こることであり、ここで操作を終了すると単に1fのジャンプと同等の高さのもの、またはフルキャンセルと呼ばれます。
低いジャンプキャンセルを行うにはさらに以下の動作が必要です。
押されたShiftキーを次のフレームで解除すると、Shiftキー解除イベントが再び発動して、プレイヤーの垂直方向の速度が再び0.45倍になります。
これにより、垂直速度が加算され、1fより小さなジャンプを出すことが可能になります。
Shiftキーを解除するタイミングを変えることによって、ジャンプキャンセルの高さを決めることができます。
また2回以上解除することもできるので、普通のジャンプキャンセルより小さなジャンプを出すこともできます。
3回解除する操作があるとダブルキャンセル、4回解除する操作があるとトリプルキャンセルと呼びます。よってダブルキャンセルは(1+n+o)、トリプルキャンセルは(1+n+o+p)と表記出来ますね。
垂直方向のスピードが0になるまでの間でしか出来ないため、無限に解除する操作が行えるわけではありません。
フルキャンセルのもう一つの用途
フルキャンセルは、1フレームジャンプと同等の高さを出すだけでなく、蔦でのジャンプ保持にも役立ちます。

Shiftキー1つだけでジャンプキャンセルを行える?
前文でジャンプキャンセルを行うには2つ以上のShiftキーが必要と書きましたが、実は1つだけでもできます。ただこれには同じフレーム内で離す動作と押す動作をする必要があるので安定はしません。
よく4.5マスなどを上る時に二段目で小さいジャンプが出ることがありますよね。実はこれが原因なのです。
アイワナは50fpsなので、1秒/50fpsで0.02秒、つまり20ミリ秒の間でこの動作が行えれば可能です。
第3章. 縦ドット(小数点以下座標)
※以下「小数点」と表記します。
プレイヤーは静止している状態において、ブロック上の整数座標にいることはなく、常に小数点以下座標が存在します。
ブロック上に静止にしている状況におけるプレイヤーの小数点Y座標の範囲は、[x.1 ~ x.5]です。
GameMakerのY座標は特殊で、上から下に向かって数値が増えるため、数値がより低いものほど高い座標にいる、ということになります。言い換えると、Y座標が逆になっています。
例えば、Y座標 1.2 と 1.5を比べた場合では、1.2の方が高い位置にいます。
図に直すとこのような感じです。

この座標平面の第四象限がアイワナの画面と思っていただけると分かりやすいかと思います。
こういった座標平面を画像座標と言い、数学で扱われる座標平面は数学座標と言います。
i. 静止しているプレイヤーの小数点の範囲が常にx.1からx.5の間である理由
GameMakerは、2つのオブジェクトが0.5ピクセルより大きく重なったときにのみ、衝突と判定します。
言い換えれば、プレイヤーが0.5ピクセルより大きく重なったとき、プレイヤーは地面に「埋まっている」ことになります。
プレイヤーは、次のフレームでの位置が地面上にあるとき、つまり垂直方向の速度が0に割り当てられているときのみ「地面にいる」とみなされます。プレイヤーの重力は0.4なので、プレイヤーが地面に立っているとき、現在位置に0.4を足した位置が、地面に張り付いているかどうかを調べ続けることになります。
ここから、地面と0.1~0.5ピクセル重なったときが安定した状態であることが分かります。
従って、プレイヤーの通常の小数点の範囲は[x.1 ~ x.5]であるのです。
ii. なぜ多くのアイワナはx.4から始まるのか
これはセーブした時、小数部分が直接四捨五入され、座標の整数部分のみを保存するからです。そしてリセットされると、ゲームはプレイヤーの整数座標位置だけを読み取ります。
このとき、プレイヤーを保存した座標に置くと、プレイヤーの小数部分は0になります。
しかし、小数部分が0というのは安定した[x.1 ~ x.5]の小数点の範囲ではないので、プレイヤーは次のフレームで0.4ピクセル(重力0.4)下がります。
これによって小数点がx.4になる、ということです。
リセット直後、プレイヤーが浮いているイメージを視認することができると思います。
初期小数点はx.4だけではない?
初期小数点はx.4だけではなく、空中でセーブするなどの工夫でx.2にすることが可能です。
プレイヤーの0.4ピクセルの落下は、プレイヤーが地面にいることを基準にしています。 0.4ピクセルの落下の後、プレイヤーが地面にいなければ、プレイヤーは次のフレームで0.8ピクセル落下し、合計1.2ピクセルの落下となります。
このときプレイヤーが地面にいれば、プレイヤーの小数点はx.2になるのです。
これにより、地面から1ピクセル離れたところでセーブするとx.2にすることが出来ると分かります。
第4章. バニーホップ
よく「バニホ」と略称して使われることが多いです。
この用語も有名なので殆どの方が知っているでしょう。
通常より高い座標を取得できることが特徴です。
基本的に、一度ジャンプしてから地面に着地する瞬間に再びジャンプすることで使用可能です。

最も有名な使用例

通常より高い座標にいるため、針の最後に当たらない
バニーホップの基本事項
まずバニーホップとは、小数点以下Y座標に関係するものです。
ブロックが偶数座標の場合、小数点以下[-x.5 <= n <= x.1]、奇数座標の場合[-x.5 < n <= x.1]の間でジャンプした時、バニーホップと呼びます。
これを踏まえると、一般的に知られている1ピクセル上に上昇できるというのは間違いである事が分かります。(x.5から-x.5の座標でバニーホップできた場合を除く)
また上記のことから、バニーホップには強弱が存在することが確認できます。

通常では取れない小数点以下x.06の座標でジャンプしているが、
納豆配置を超える高さには達していない
-x.5でバニーホップした場合が一番強いものになり、これはvfpi(vertical floating point inaccuracy) bhopと海外では呼ばれ、特殊なものになっています。これに関しては、バニーホップの原理と、第9章にて詳細を説明しています。
バニーホップの原理
これは、第9章の基本にもなっています。合わせてお読みください。
まずプレイヤーのブロックとの判定に関する説明をします。
プレイヤーは、もし1ピクセル下にプレイヤーのy座標があった場合に、ブロックの内部にプレイヤーがいるかを確認してジャンプの可、不可を判断しています。
例として、jtoolを用いり説明します。
jtoolの初期ブロックのy座標は416にあり、プレイヤーがそこに立つ場合、プレイヤーの座標は407.4に存在することになります。これは、プレイヤーのOriginが9ピクセル上に設定されていて、その座標をオブジェクトの座標として計算するからです。

この場合、プレイヤーが1ピクセル下の座標に存在した場合にブロックの内部に存在するかを確認するため、1ピクセル下げた408.4の座標をチェックすることになります。この時、プレイヤーの足元は416.4にあり、ブロックの内部にいると判断できる為、ジャンプが可能と分かります。逆に言えば、プレイヤーの座標が406.4にあった場合、1ピクセル下げた時の足元は415.4でブロックの内部には存在しないので、ジャンプをすることはできないと判断することができます。
小数点座標の端数の銀行家丸め
プレイヤーが406.5の座標でジャンプする場合に確認する座標は407.5で、足元は415.5にある為ブロックの内部に存在しない事になりますが、これはジャンプができないものでしょうか?
答えは否です。実はsolidの判定をするときに、小数点以下の座標は四捨五入された状態で処理されます。407.5は結果的に408に四捨五入されるので、ブロックの内部にいることになります。
※この後が一番大事です。
ではブロックを1ピクセル下げてみましょう。
ブロックが417の座標にあり、プレイヤーが407.5でジャンプする場合はどうでしょうか?1ピクセル下げた408.5を四捨五入し、409になりジャンプができるはずです。
しかし、これが出来ないのです。しかも、四捨五入した数値は408になります。四捨五入とは一体…?と疑問に思いますよね。
この原因は、GameMakerが銀行家の丸めという特殊な四捨五入のようなものを用いているからです。
銀行家の丸めとは
端数が0.5より小さい場合は切り捨て、大きい場合は繰り上げ、ちょうど0.5だった場合は、切り捨てか繰り上げした時、一番近い偶数になるようにするものです。これに従うと…
408.75 → 409
408.5 → 408
408.25 → 408
408.0 → 408
407.75 → 408
407.5 → 408
407.25 → 407
…となります。
よって408.5は一番近い偶数の408を取り、結果的にブロックの内部には居ないことになるためジャンプができないのです。
このことから、奇数座標での-x.5のバニーホップは機能しないことになります。これが最初に書いた、偶数と奇数でのバニーホップできる座標の違いの理由です。
長くなりましたが、これがバニーホップの原理です。
バニーホップの猶予フレーム
バニーホップは、着地してからすぐジャンプをしなければならないという印象が強い為、猶予フレームも1フレームしか無いように思えます。
しかし、場合によっては猶予が増える場合があります。
まず、プレイヤーはブロック上にいると判断した時、垂直方向のスピードを0にします。
着地するブロック座標位置を416としましょう。この時、プレイヤーが小数点以下座標 -x.5(406.5)で着地する場合、垂直方向のスピードを0にして、安定した小数点以下を含む座標[407.1 ~ 407.5]になるまで重力0.4を足すという2つの動作を繰り返します。
従って、

となるため、バニーホップの猶予が3フレームあることが分かります。ただ、特定の座標の場合の猶予は1フレームだけですね。jtool内のBhop項目でgoodが出るのは、最初の1フレームのみのようです。
第5章. A/Dトリック
簡単に説明すると、プレイヤーを1ピクセル前後に移動させる技術です。
常時ドット調整をすることを出来たり、方向キーと組み合わせると通常より前に出ることが出来る為、様々な配置が可能になることが特徴です。
基本的に、プレイヤーが地面についている場合のみ有効です。

A/Dトリックの原理
基本的にプレイヤーの座標を+1か-1移動させるもので、元の移動速度に加算することができます。
(例えば、右キーとDを同時に押した場合、1フレームに4ドット進むことになります。)
またリフト内では常にA/Dが使用できるため、ブロックに着地していなくても、リフト内であれば使用することが可能です。
jtoolでの特殊な機能
jtoolではM/Nキーで0.5ピクセルずつの移動が可能なので、A/Dと組み合わせて最大で+1.5速度を加算することが可能です。

第6章. ダイエット
ダイエットは、プレイヤーのx座標が.5にある場合、判定が1px小さくなる技術です。GameMaker8(8.1)とStudioでは座標の処理に違いがあり、基本的にGM8では右を向いているときに、Studioでは左右どちらでも可能です。

判定が横に小さくなっている為、ブロックに頭を打たない。
(vfpiを使うとダイエット無しでも可能)
主に.5のスピードのリフトなどを用いり、.5のx座標を取得できます。
※.1のスピードのリフトを用いて.5にしてもダイエットすることはできません。(0.1を2進数にした時の循環小数による誤差?)
ダイエットの原理
GameMakerは、オブジェクトが0.5ピクセルより大きく重なった場合に衝突判定が行われる、ということを小数点座標の章で説明しました。
それを踏まえると、プレイヤーのx座標が.5になった場合、左右の0.5ピクセルは判定されないことになります。
結果的に、合わせて1ピクセル分の判定が無くなるのです。
GM8での特殊なダイエットの使い方
GM8使用のアイワナでは、左を向くと元に戻る現象を利用し、壁に埋まることができます。

Dトリックを使うことによって埋まった状態からジャンプができる
第7章. 降りジャンバニーホップ
よく「降りジャンバニホ」と略称して使われることが多いです。
降りジャンバニーホップはバニーホップにとても似ています。
ドットや、V-Stringが悪い場合に使われることが多いです。


降りジャンバニーホップの原理
バニーホップと同様の小数点以下座標で発生します。
バニーホップは地面から少し離れていた時にでも衝突判定があり、高い小数点以下座標を取得できるものです。
降りジャンバニーホップはそれに加え、地面と衝突した時速度が0になるということを利用しています。つまり、通常より高い位置から横移動を開始することが可能になるということです。
第8章. カクタス
名前だけはよく知られていると思います。
簡単に説明すると、通常では出せない高さのジャンプを出す技術です。

もっとも最も有名なカクタス必須配置
カクタスの原理
カクタスの原理はジャンプキャンセルと同様です。
例えば、5フレームのジャンプを出した数フレーム後にShiftキーが解除されると、プレイヤーの垂直方向の速度が再び0.45倍になり、5フレームのジャンプより小さいジャンプを出すことができます。
これを踏まえると、ジャンプキャンセルは1フレームのカクタスとも言えることが分かります。
ジャンプキャンセル同様、3回解除する操作があるとダブルカクタス、4回解除する操作があるとトリプルカクタスといった名前があります。ダブルカクタスは(m+n+o)、トリプルカクタスは(m+n+o+p)の表記になりますね。
カクタスの様々な用途
カクタスの機能として、ジャンプの高さの制限がよく知られていますが、その為だけではありません。
カクタスはプレイヤーの垂直方向の速度を変えることができ、必然的にそれに伴うV-Stringも変化させることになります。
まずはこのGIFを見てみましょう。

GIFの説明にもあるように、この配置は(1+3+2)カクタスによって可能です。
しかし、埋まり納豆の一番上に近づけるジャンプは、通常のジャンプキャンセル(1+3)で十分なのです。大きく飛んだ方が遠くに飛ぶ為には有利な気がしますが、なぜさらに減速が必要なのでしょうか?
まず通常のキャンセルとカクタスを使った場合、どこの座標まで下れるのかを比べてみましょう。


通常のジャンプキャンセルはカクタスの一部ですし、(1+3+2)のカクタスはダブルキャンセルとも呼びます。ここでは説明の都合上、(1+n)のジャンプをジャンプキャンセルと呼び、ダブルキャンセルを(1+m+n)カクタスと表記しています。
これを比べると、(1+3+2)カクタスの場合の方が下の座標に到達できていることが分かります。
二段目で最奥に行ける1フレームジャンプを出すためには、通常のジャンプキャンセルで到達できる座標では不十分である為カクタスを使う必要があります。
章初めに貼った、Butterfly Novaのジャンプもこれと同様です。上部に天井がありジャンプの高さが制限されるため、カクタス無しでは十分なV-Stringを取得できません。言い換えれば、天井がなければカクタス無しでも十分なV-Stringを取得できます。
第9章. プレイヤーY座標x.5における特殊な衝突判定
第4章 バニーホップ編の先に見ておくと理解が深まります。
まずはこのGIFをご覧ください。

針の先端1ピクセルでのみジャンプできる
ブロックの上に針があるにも関わらず、死ぬことなくジャンプ出来ています。なぜこのようなことが可能なのでしょうか?
これは、プレイヤーのY座標の整数値が偶数で、小数点以下Y座標がx.5になった時のみ発生する現象です。Collisionイベントとプレイヤーのブロックとの判定を見比べると、原理を簡単に説明することができます。
プレイヤーはブロックにおいて、もし1ピクセル下に存在する場合、そのオブジェクトの内部にいるかどうかを判断してジャンプの可、不可を判断するということと、オブジェクトと0.5ピクセルより大きく重なった場合に衝突判定が起きるということを前に書きました。
この二つを利用します。
まず、プレイヤーが針の先端の1ピクセルと衝突しない座標を確認していきましょう。針の先端の1ピクセルがあるy座標を415とします。
プレイヤーは0.5ピクセルより大きく針と重なった場合死んでしまうので、n<=414.5であることが分かります。
次に、プレイヤーがブロックでジャンプ出来る最大の座標を確認しましょう。ブロックの座標を416とします。
銀行家の丸めに基づき、プレイヤーの足元の座標が414.5の時が最大というのが分かります。
この二つの要項を重ねると、プレイヤーの足元がちょうど414.5の時、針にも当たらずブロックからもジャンプ出来る、という状態を作りだすことが出来ます。これが針の上でさえもジャンプできる原理です。
プレイヤーの座標が奇数の時不可能なのは、銀行家の丸めから説明が付きますが、詳しくはバニーホップ編をご覧ください。
一般的にこのようなジャンプは「vfpi bhop」と呼ばれます。
また、vfpiを使用すると、1マス上げた上下4連針(Leehe Triple Diamond)を超えることができます。

ただこれには複雑な小数点以下座標の処理が関わってきます。その影響で、この配置名の由来であるI wanna break through Leehe Trapでは不可能なのです。詳しくは第15章をご覧ください。
第10章. 蔦によるプレイヤーへの効果
蔦は主に壁や空中に吊るされていて、左右に飛ぶこと出来るオブジェクトです。
蔦はプレイヤーに様々な効果をもたらします。
プレイヤーへの蔦の効果
プレイヤーが蔦と衝突している時、プレイヤーの垂直落下速度が2に固定されます。
これを用いて、プレイヤーの垂直速度を減速させ、様々な配置を可能にすることが出来ます。
またプレイヤーが蔦で飛んだ時、プレイヤーに垂直上方向に9、水平方向に15の速度を与えます。
これにより、本来通れない隙間などを通ることが可能になります。

エンジンによる蔦の仕様
蔦の判定はエンジンによって異なり、distance_to_object関数 か place_meeting関数 を使用しているかに依存しています。
distance_to_object関数 を使用した蔦はブロックが付いていても上下から触れることができますが、place_meeting関数を使用している場合はできません。
第11章. ポーズ機能
ポーズ機能はゲームを一時停止することができるものです。
基本的に使用できるゲームはPキーで出来るものが多いと思います。
以下は、そのポーズ機能を応用した技術になります。
i. ポーズジャンプ
通常、2段ジャンプを出す場合は一度Shiftキーを解除し、それから再び入力する必要があるため、どうしても1フレームのジャンプ間隔が出来てしまい、それ以上早く飛ぶことができず、少し減速した状態で飛ぶことになってしまいます。
どうにか間隔を0にすることはできないのでしょうか。
この問題を解決するためには、Shiftキーを解除するという動作を省けば良いことが分かります。
これに対して一番効果的なのが、ポーズ機能を使うことです。
ポーズジャンプの使用方法
Shiftキーを押してからポーズを押し、Shiftキーを解除した後ポーズも解除すると、ジャンプの解除される処理は一切行われません。
これにより間隔なしのジャンプが可能になり、小数点.4でもバニーホップ無しで4.5マスを上ることができたり、バニーホップを使えば針付きの4.5マスジャンプを超えることもできます。

ii. ポーズして蔦を掴む事のメリット
この技術はGameMaker Studioでのみ機能します。
ポーズ機能を使うことにより、中途半端なジャンプで蔦をつかんでも二段目を残して飛ぶことができます。
Shiftキーを離したあとポーズを行ってからShiftキーを入力し、ポーズを解除して蔦を掴むと行えます。

iii. ポーズの乱用
ポーズをし、解除したあと直ぐにポーズを行うという動作によって、コマ送りのような状態になり、難易度を弱めることができます。
実際に使用されている動画
正し、水中せま斜めなど、人力ではなかなか厳しい操作を行う時に使うのが常識的で、出来れば普段の使用は控えたいところです。
多くのGameMaker Studio用のエンジンではこれが対策されているため、使用できるのはGameMaker 8用の一部エンジンのみです。
第12章. Dual Collision(二重衝突)
簡単に言うと、プレイヤーとオブジェクトとの衝突順序に関係する特殊な判定のことです。
Dual Collisionの説明、原理
まず初めに、プレイヤーのオブジェクトとの衝突について見てみましょう。
基本的にプレイヤーは、
水平方向のブロックの検知
垂直方向のブロックの検知
という順序で判定が行われます。
まずはこのGIFを見てください。

針の中にある壁を触り、ドットを取得出来ています。
なぜ針に当たらず、壁を触ることが出来ているのでしょうか?
その原因は、上記に示したプレイヤーの衝突順序にあります。
まずプレイヤーは、針に触れる前に水平上にあるブロックに触れます。普通はその次の処理で針に当たって死んでしまいます。
しかし、水平方向に衝突するフレームと同じフレームでジャンプを行うと、8ピクセル上部にある天井ブロックによって、2番目の垂直方向に対する衝突判定が行われます。この時、プレイヤーは既に針を抜けています。

結果的に針に当たらずにドットを取ることが可能なのです。

垂直上にある針に当たる前に横の壁が先に判定されるので、横に吸い込まれるようにして届くことが可能になっています。
第13章. PTJ (Platform Triple Jump)
PTJとはリフトを用いり、三段ジャンプを行う技術のことです。言い換えると、普通ではありえない高さからジャンプを始める方法です。I Wanna Makerではリフトの仕様が異なる為、使用することはできません。

PTJの原理
まず、リフトオブジェクトのコードを見てみましょう。

分析すると、リフトから4ピクセル以内であればリフトに乗っているという判定が行われるようですね。 つまり、リフトから4ピクセル以内でジャンプ出来れば、バニーホップの上位互換のようなことが行えるということになります。 しかし、これには幾つかの条件があり、
前のフレームでリフトにいたこと
ジャンプを4px以内に収めないといけないこと
この2つが必要になります。
これに対応したジャンプが1フレームジャンプです。 1フレームジャンプの最初のフレーム高は3.425なのでちょうど上記条件を満たすことが出来ます。
PTJの猶予は1フレームしかなく、1フレームジャンプを行った1フレーム後にジャンプを行わなければならないので、非常に操作が難しいものになっています。テンキーを活用することによって容易になりますが、ここでは割愛します。
しかし、上記の条件を満たせばよいので、上部にブロックを設置することでもPTJは可能です。これを利用すると、このような不思議ことができます。

毎フレームジャンプを出すことによって浮いたような状態を作れる。
特殊なPTJ
リフトの性質上、リフトの上に立っているとき、プレイヤーのy座標は常に0から0.4の間であるため、一般的なPTJの可能な小数点以下は2つしかありませんが、特殊なケースとして、それ以外の小数点以下も実現できます。
プレイヤーがブロックとリフトの間にいる時、小数点以下はブロックの方を採用します。よってリフトでリセットされることはなく、またそれと同時にリフト上にもいるので、PTJを出すことができます。
第14章. 衝突順序の利用
GameMakerは、先に作成されたオブジェクト(オブジェクトのインスタンス数が小さい)の順に衝突判定が行われます。
例えば、針の後にブロックを作成したとします。
すると…

このように、ブロックの先端につく前に死んでしまいます。
この点では衝突順序はとても不便なものですが、場合によっては有用です。

TAS動画から抜粋。
このアイワナは本来は不可能なのですが、針とワープの衝突順序によって奇跡的にクリア可能なことが分かりました。この場合は、ワープの後に針が作られたことによってワープの処理が優先されています。

横ドット、V-Stringを合わせると、1ピクセルだけワープに触れられていることが分かります。
第15章. GameMakerの不正確さとそれの利用
i. 小数点以下の僅かな誤差
プレイヤーの1段目の速度は8.5、重力は0.4、シフトを離した場合の減少は0.45倍である事はこの記事の最初に説明しました。
これに従うと、理論上、プレイヤーの小数点以下の最初の7桁だけが変更できることになります。
ところがゲーム内では、小数点以下が変化するたびに、小数点以下の下7桁以降の数字が大きく変わります。
この原因は、GameMakerの不正確さにあります。従って、プレイヤーの小数点以下の数値(通常は 0.0001 ピクセル未満)は理論上のものと異なります。
この現象はほとんどのアイワナの場合無視できるものですが、vfpiのような完璧な小数点を必要とするものに関しては影響が大きいのです。
vfpi、vfpi bhopを行うためには、小数点以下が完璧に.500000...である必要があるので、0.000001ピクセルでもずれが生じた場合、失敗することになります。
理論上では、.50000…に到達できる組合せは多数存在します。しかし、GameMakerによる約0.0001ピクセルの誤差により、とても限られたものになるのです。
なぜこのような誤差が生じるのでしょうか?
それは、浮動小数点の誤差数によるものなのです。
基本的にパソコンは数値を2進数化して保存します。大体の場合、10進数を2進数に直すと無限小数になります。
しかし、パソコンは無限の桁数を保存できないので、どこかで小数点を切り離し捨てる必要があります。
これに従うと…

…となります。これが誤差が起きる原因です。
小数点以下誤差による配置とプレイヤーへの影響
小数点以下誤差の数値は、整数部分によっても変わります。
つまり、プレイヤーの座標.4を表すことができる数値は複数あることになります。(x.399993896…や x.400024414…など)
これにより、配置がある座標によって可能か不可能な場合が存在します。
Leehe Triple Diamondはこれの典型的な例です。
また一部の座標間隔では、小数点誤差が同じになります。
その間隔は2^nの座標(128~256, 256, 512)で起こります。
GameMaker8とStudioの変数管理方法の違い
GameMaker 8とStudioでは、変数管理の方法に違いがあります。
変数管理にはfloatとdoubleという2種類の方法があります。
float
32bit (約4バイト)で変数を保存する。
double
64bit (約8バイト)で変数を保存する。
比べると、doubleのほうが多く変数を保存できることが分かります。
GM8では、基本的に組み込み変数(x, y, speedなど)とカスタム変数(自分で作れる変数)の両方をdoubleで保存します。
しかし、GMStudioでは組み込み変数はfloat、カスタム変数はdoubleで保存されます。
GMStudioの方が、組み込み変数の管理に関してGM8よりも劣っているのです。よって、オブジェクトの座標はGM8の方がより正確に反映されていることになります。
ii. ファーランド
i で説明した通り、GameMakerが保存できる数値には限界があります。
その為、Y座標の整数値が大きくなればなるほど、小数部分の精度が悪くなり、それに伴い目に見えるほど大きな現象が発生します。例えば、垂直方向の速度が特定の値(例えば2、4)より小さいとき、プレイヤーのy座標は変化しません。

勿論、x座標でも変化が起きます。例えば、x座標が非常に大きい場合、プレイヤーの水平速度は4になります。

見て分かるとは思いますが、この技術はほぼ役に立ちません。実質バグだらけのアイワナで、何もかもがめちゃくちゃになっています。
iii. GameMakerの数値誤差によるプレイヤーへの影響
元記事でGMS1に関しての説明がなかったので、ここではGMS2を基本に説明していきます。
1. GameMakerの重力方向の誤差と285万年トリック
GameMakerの重力方向は270度(鉛直下向き)に設定されています。
しかし、GameMakerの数値誤差により、完全な270度ではなく、左右どちらかに僅かにずれています。(GM8では左向き、GMStudio2は右向き)
GM8では約10^-14、GMS2では約10^-7誤差があります。
この原因については、まだ正確には特定出来ていません。(円周率と三角関数の誤差による説があります。)
これに伴い、水平方向にもこの誤差の影響が出ます。
つまり、プレイヤーの歩くスピードは0でも3でもなく、常に重力によってこの誤差があるのです。
しかし、プレイヤーは毎フレームごとに水平スピードを強制的に戻すので、誤差をそれ以上加算することはありません。従って、誤差は上記数値で安定します。非常に小さい誤差の為、x座標の数値が少しでも大きい場合にはその小数部分の精度が悪くなり、プレイヤーへの影響はほぼありません。
しかし、x=0, 1などの小さい整数値の場合には、影響が表れ始めます。
誤差分のスピードが水平方向に加算されるのです。

GMS2では1フレームで約2*10^-7ピクセルほど移動するようです。
アイワナのフレームレートは基本的に50fpsなので、(2e-7)*50=1e-5、よって1秒間に10^-5ピクセルほどずれます。
上記の誤差を用いてダイエットの座標、x=.5の取得を試みてみましょう。(0.5/1e-5)/(60*60)=13.888…
となるので、約14時間かかることになります。
またGM8ではこれよりも遅いです。海外の方の測定によると、10^-13ピクセルを動かすのに約18秒かかるようで、これをもとに計算式を立てると、
(18*(0.5/(1e-13)))/(60*60*24*365)=2853881.2….
になり、約285万年もかかることになります。恐ろしいですね。
下記動画リンクは、これをシミュレーションしたTASになります。
[TAS] It's uncanny how easy it is in 5.7 million years
なぜGM8とGMS2の間にこれほど大きな差があるのかは詳しくは分かりませんが、長年のGameMakerのアップデートによって変更が加わったと類推されます。実際に、GM8では組み込み変数はdouble、GMSではfloatが採用されています。
2. move_contact_solid関数による誤差
1では重力方向の誤差でプレイヤーのx座標をずらす手段を紹介しましたが、もう一つ方法があります。それは、低い座標で頭をぶつけたり、地面に着地したりすることです。これは、move_contact_solid関数が影響していると考えられます。なぜなら、多くのエンジンではこの関数が着地や頭をぶつける処理を行い、方向も関連しているからです。ただし、これは重力の影響とは異なり、一度の頭をぶつけただけではx座標は変化せず、何度か頭をぶつける必要があるようです。従って、これについては仮説にすぎず、本質的な原因を理解するにはmove_contact_solid関数の具体的なコードを調べる必要があるかもしれません。
同時に、この現象はmove_contact_solid関数の問題であるため、水平方向の壁に沿っている場合もy座標に影響を与える可能性があります。つまり、非常に低いy座標で壁に貼り付いた場合、y座標にも少しの変化が生じる可能性があります。
iv. 蔦によるダイエットの取得
iiiでは、プレイヤーは毎フレームごとに水平速度を強制的に戻すので、誤差が一定の値になると説明しました。しかし、強制的に戻すプロセスを無くすことが出来れば、誤差数値を大きくすることが出来るのではないでしょうか?
実際に、これを可能にする方法があります。それは蔦を使うことです。


ここのコードから、プレイヤーが蔦から1 ピクセル未満の地面に立っている場合、蔦の反対の方向キーを押し続けると、毎フレームごとの水平速度のリセットを回避できることがわかります。この時、重力による数値誤差を連続的に加算することができ、段々とx座標の変化速度が速くなります。GMS2ではダイエット(x.5)を取得するまでにかかる時間は5分程度であり、実用性が大幅に向上します。もちろん、GM8での時間はこれよりも長くなりますが、285万年よりも遥かに短い時間であることは間違いありません。
v. 不正確なダイエット
x.49997、x.499999 などの不正確なダイエットのことです。不正確なダイエットの特徴は、ジャンプの途中で突然正確なダイエット(x.5)に変化するなど、特定の状況下で不正確なものから正確なものに変化する可能性があることです。これは何の役に立つのでしょうか?
例の一つとして、埋まり納豆配置があります。正常なダイエット状態では最大2.78125ブロック (A/Dトリック無し) までしかジャンプできませんが、不正確なダイエットでは2.8125ブロックまでジャンプできます。
この原因は考えが付きます。x.5の状態ではプレイヤーが1ピクセル分判定が無くなりますが、x.4999…などはまだ判定があります。例えば、乗っているブロックの一番端の座標が100で、プレイヤーの一番左のx座標が100.5と100.4999..だった場合、100.5の場合は1ピクセル分判定がなく、ブロックから落ちます。しかし、100.4999..の場合はまだ判定が残っているので、ブロック上にあり、結果的に普段よりも前に出ることが出来ます。
この場合では不正確なダイエット、と呼ぶのは少し語弊がありますね。
不正確なダイエットは、正確なものと不正確なものの両方を利用することができます。不正確なダイエットは浮動小数点誤差を使用し、x座標を正確に丸めます。つまり、プレイヤーが特定の x 座標精度制限 2^n を超えると、x 座標の精度が低下します。精度が低下するとx座標は丸められ、x.5 に四捨五入されます。このことから、移動中に 2^n の x座標精度制限を確実に超えてしまう場合があることがわかります。また、x座標の精度制限 2^n ごとに、x.5に丸めることができる座標が異なり、精度の制限が低いほどx座標はx.5 に近づきます。 つまり、不正確なダイエットで同じようには機能しない横ドットが多数あり、各横ドットは特定のx精度制限でのみ機能します。
これを利用した配置を一つ解説します。

正確なダイエットのまま蔦を掴むと、下のようにダイエットの影響によってGIFよりも埋まってしまっていることが分かります。
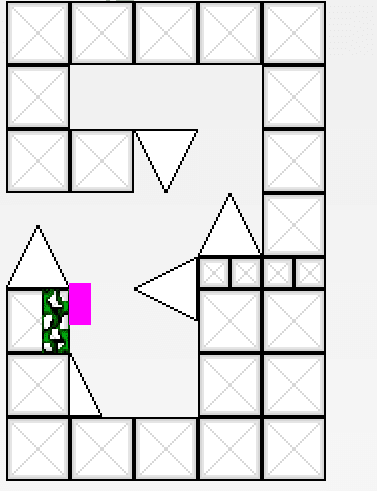
ここで不正確なダイエットを用いり、これよりも右の位置で飛ぶことが出来ます。蔦でジャンプした後、座標はx.5に丸められ、正確なダイエットとなるので超えることができます。
vi. 最高高度のPTJ
第13章では、PTJについて触れ、その上限が4ピクセルであることを書きました。しかし、PTJの条件による制限から、PTJの最大高さ(4ピクセル)を達成することは現実的ではないのです。 しかし同時に、その章では任意の小数点以下でPTJをする方法も紹介したので、この方法でPTJの最大高さを出すことに成功する可能性もあります。
しかし、それはこの章と何の関係があるのでしょうか? 最大のポイントは、最大高度のPTJの応用は、浮動小数点誤差を巧みに利用しているということです。 ブロック上にある上向き針の場合、1列目の高さは2ピクセル、2列目の高さは4ピクセルです。通常、PTJの高さは1列目の2ピクセルを簡単に超えてしまうので、それを超える為にPTJを使います。しかし、2列目をよく見ると、PTJの最高高度である4pxとまったく同じ高さであることがわかります。 ということは、PTJの最も高い高さで2列目を超えることが出来るということとでしょうか? これは残念ながら出来ません。なぜなら、GameMakerの銀行家の丸めによってy座標 約x.5の判定に対する奇数と偶数の座標の差をカットしてしまうからです。仮に行ったとしても、単に針を超えるだけでPTJが失敗するか、PTJは成功するが針に当たるかのどちらかになります。 なので、この方法は不可能であるように思えます。
しかしよく見ると、針の衝突判定とは異なり、PTJのジャンプ判定は、衝突判定をする前に、プレイヤーのy座標に4を足していることが分かります。この+4を使って何かできるかもしれません。 小数点以下が x.4999...の座標と仮定すると、この座標は厳密にはx.5未満なので、整数部が偶数、奇数であろうと針には当たりません。 ただし、この座標に4を加算した後、ちょうど2の累乗を超えて x.5 に四捨五入された場合でも、PTJを起こすことができます。例えば、y座標 254.499999..はy座標 255の針と当たりませんが、y座標 258でPTJを出すことができます。
つまり、これは浮動小数点誤差の応用例なのです。
vii. I Wanna Makerにおける浮動小数点エラーと衝突判定
I Wanna Makerの開発者はなんらかの理由によりエンジンを書き直しました。その結果、IWMでの浮動小数点数の動作が通常のアイワナとは異なります。この違いは2つの要因によって引き起こされています。
1つ目は、変数を格納する方式が異なることです。GM8では、組み込み変数はすべてdoubleですが、GMSではすべてfloatであることがわかっています。しかし、IWM では、座標だけがfloatのままで、速度と重力は両方ともdoubleとして保存されます。この動作は非常に奇妙で、IWMの開発者が何らかの理由で組み込み変数の速度と重力を使用せずに、カスタム変数を使用して速度と重力を保存したためではないかと思われます。
2つ目は衝突判定の違いです。IWMでのブロックの判定は他のアイワナと同じですが、針の衝突判定は少し異なります。IWMでは、プレイヤーの座標が奇数である場合、プレイヤー下部の針とのy座標x.5の衝突は考慮されませんが、他のアイワナでは衝突と判定されます。
また、ダイエットに関しては、IWMでは禁止されています。これはプレイヤーの特性を直接改変したものではなく、プレイヤーがx座標x.5を取得することをを禁止するというものです。しかし、不正確なダイエットは引き続き使用できます。
第16章. 小数点以下の調整
プレイヤーの小数点以下座標を見ることが出来ない場合に、何らかの手段で一定の範囲内に収めることが出来る技術を紹介します。
i. 最も簡単な小数点調整
1. リフト
リフトにプレイヤーが乗ると、小数点以下を強制的にx.0に戻し、x.0とx.4を繰り返します。これにより、x.4に調整することが出来ます。(x.0で抜けた場合、不安定な小数点になるため、重力によって+0.4が行われます。)
I Wanna Makerのリフトはこの機能がないので注意しましょう。
2. ワープ
多くのアイワナのワープは強制的に整数座標上に移動させるので、x.4に調整することが可能です。
3. セーブ&リセット
セーブした後、リセットするとx.4に調整することが出来ます。これは、ゲームが整数座標部分しか保存しないためです。1ピクセル上でセーブするとx.2にすることも可能です。(第3章参照。)
ii. フレームコントロールによる調整方法
針ゲの動画を見ていると、ある配置の前で一定のジャンプをしている時がありますよね。これは、特定のフレームを出すことによって調整する方法を使っています。

(4フレーム フルジャンプ*2 4フレーム フルジャンプ*3)
この方法によって、元の小数点座標[x.1 ~ x.5]から92.5%の確率で[x.1 ~ x.2]の間にすることが出来ます。
この原理は、あるフレームでジャンプすることによる、y座標へのの影響を利用することです。例えば、天井がない状態でフルジャンプを行うと、y座標は-0.1減少し、1fを出すと-0.05減少します。
プレイヤーの小数点以下座標が [x.3 ~ x.5] の間にある場合、4フレームのジャンプでは小数点以下座標が変化しません。また、[x.1 ~ x.3] の場合、4フレームのジャンプすると小数点以下は x.385より大きくなります。つまり、4フレームのジャンプは小数点以下座標の範囲を狭めることができるフレーム数です。つまり、プレイヤーの小数点を見ることが出来なくても、4フレームのジャンプを1回行うだけで、[x.3 ~ x.5] の間に制限できます。
4フレームのジャンプではこのような性質がありますが、他のフレームではどうなるのでしょうか? また、なぜこのようなことが起こるのでしょうか?
以下の図で分析してみましょう。

この図は、ブロックに対するプレイヤーのいくつかの重要な高さの値を示しています。-0.5 は、プレイヤーがブロック上にいるときの下限座標を表します。-0.1 から -0.5 までの間隔は、安定した小数点以下座標間隔なので、変わることはありません。変化する可能性のある小数点以下座標の範囲は [.1 ~ .5] です。+0.3 から -0.1 の範囲は、最初の不安定な小数点以下座標の部分です。プレイヤーがこの範囲にいる場合、重力により +0.4 され、[x.1 ~ x.5]の間の安定した小数点以下座標が得られます。したがって、この部分で取得できる小数点以下の範囲も [x.1 ~ x.5] となります。
最後に、上の範囲を見てください。プレイヤーが +0.5 ~ +0.3 の範囲にいると、次のフレームでプレイヤーの速度が 0 になります。
まず+0.4 → +0.1 → -0.1、次に+0.4 → -0.3 → -0.5となります。 よってプレイヤーがこの間隔に落ちた場合、プレイヤーが得られる小数点以下の高さは[x.3 ~ .5]であることがわかります。
次に、プレイヤーが着陸可能な状態を分析しましょう。
ケース1

これが最初に考えられる着陸状態です。画像内の長方形はプレイヤーの当たり判定ではなく、ジャンプするときの小数点以下が .1 から .5 に変化するときの下限、つまり長方形の上辺はジャンプを開始した時の小数点以下が0.1のときのプレイヤーの当たり判定の下限であり、長方形の底辺は0.5のときのプレイヤーの当たり判定の下限であることに注意してほしい。したがって、長方形の下限の下の部分は +0.5 から +0.3 までの範囲内にあり、黄色で塗られている部分の長さは a (a<=0.2) であることがわかります。
したがって、次のような比較関係が得られます。
[0.1,0.1+(0.4-a)] → [0.5-(0.4-a),0.5]
[0.1+(0.4-a),0.5] → [0.3,0.3+a]
即ち、
[0.1,0.5-a] → [0.1+a,0.5]
[0.5-a,0.5] → [0.3,0.3+a]
矢印の左側がジャンプを開始した時の小数点以下範囲、矢印の右側が着陸した時の小数点以下範囲です。
この状況では、最初の着陸した時の小数点以下の範囲 (0.5-0.1) = 0.4 が、その後(0.5-min(0.1+a,0.3)) = max(0.4-a,0.2) の範囲に制限されることがわかります。着陸の場合、a<=0.2 なので、最大値 a=0.2 とすると、最小制限範囲は 0.2 と求まりますので、この場合、不確定である着陸した時の小数点以下の範囲 0.4 は最大 0.2 までに制限できます。
ケース2

この着地状態ですが、長方形は+0.5 ~ +0.3の範囲を完全に過ぎて+0.3 ~ -0.1の範囲に達しています。しかし、長方形には +0.5 制限を超えていない部分がまだいくつかあるため、<=0.2 になります。
小数点以下間の比較関係を取得すると、
[0.1,0.1+(0.4-0.2-a)] → [0.5-(0.4-0.2-a),0.5]
[0.1+(0.4-0.2-a),0.1+(0.4-0.2-a)+0.2] → [0.3,0.5]
[0.1+(0.4-0.2-a)+0.2,0.5] → [0.1,0.1+a]
即ち、
[0.1,0.3-a] → [0.3+a,0.5]
[0.3-a,0.5-a] → [0.3,0.5]
[0.5-a,0.5] → [0.1,0.1+a]
最初の 2 つの式を組み合わせると、ジャンプ開始時と着陸時の両方の比較範囲を取得できます。
[0.1,0.5-a] → [0.3,0.5]
a=0 の場合、最初の場合に相当します。つまり、0.4 の範囲が 0.2 の範囲に縮小されます。
ケース3

この着陸状態は、長方形は +0.3 の制限を超え、同時に +0.5 の制限を超えています。+0.3 の制限を超える長さは a です。この場合、a>=0.2です。
比較関係を取得すると、
[0.1,0.1+(0.4-a)] → [0.5-(0.4-a),0.5]
[0.1+(0.4-a),0.5] → [0.1,0.1+a]
即ち、
[0.1,0.5-a] → [0.1+a,0.5]
[0.5-a,0.5] → [0.1,0.1+a]
この場合、小数点以下の範囲を圧縮できないことがわかります。
ケース4

この場合、長方形は -0.1 の制限を超えており、超えた部分の長さは a です。比較関係を取得すると、
[0.1,0.1+(0.4-a)] → [0.5-(0.4-a),0.5]
[0.1+(0.4-a,0.5)] → [0.1,0.1+a]
即ち、
[0.1,0.5-a] → [0.1+a,0.5]
[0.5-a,0.5] → [0.1,0.1+a]
この状況はケース3と同じであることがわかり、小数点以下の範囲を圧縮できないということになります。
ケース5
このケースはさらに複雑です。
1.
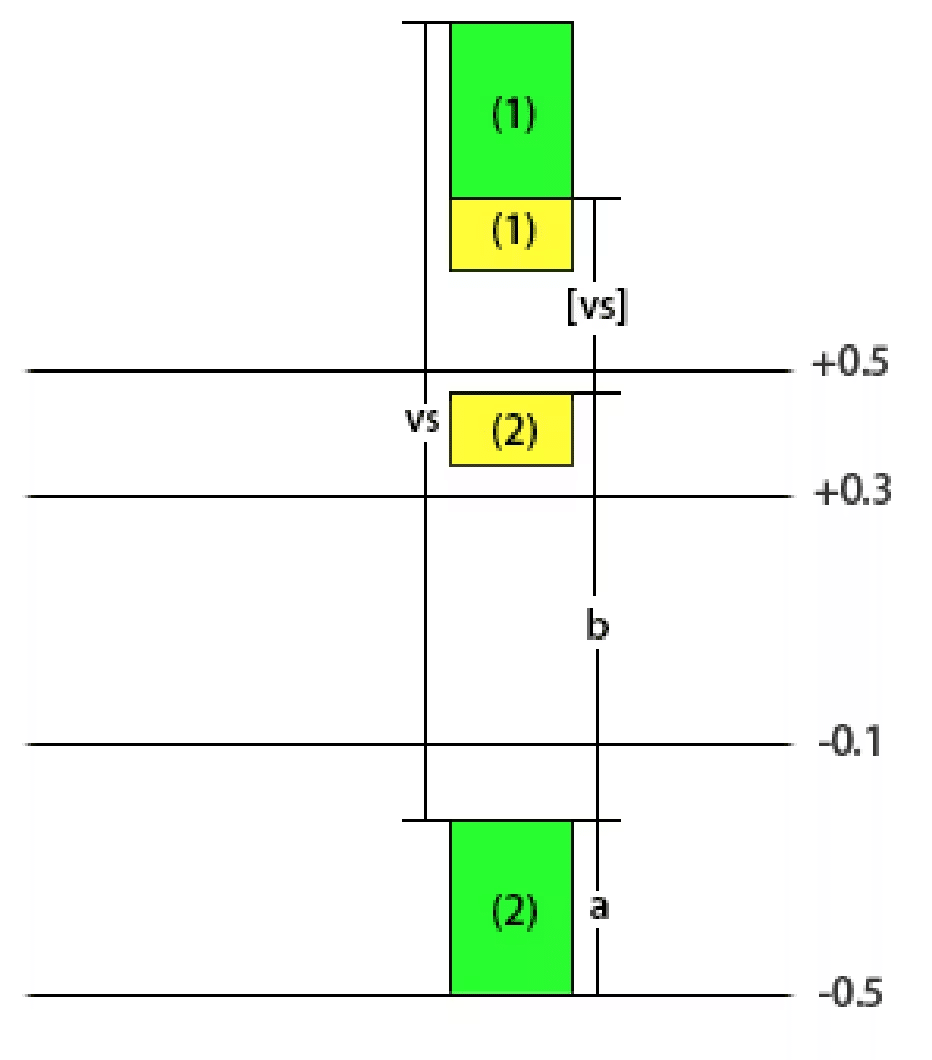
この場合、着地フレームとその前のフレームの状態を考慮する必要があります。緑 (1)の部分は緑 (2)の部分に、黄色 (1)の部分は黄色 (2)の部分に下がります。このうち、緑の部分の長さをa、緑の頂点 (2)と黄色の頂点 (2)の間の距離をb、緑 (1)と緑 (2)の距離を現在のvs (vspeed)とします。黄色 (1) と黄色 (2) の間の距離は、現在の vspeed より小さい最大の整数とし、[vs]と表記します。
変数関係を取得すると、
vs=a+b+[vs]
[vs]はvsより小さい最大の整数なので、0<vs-[vs]<1となり、0<a+b<1が得られます。
またこの場合、黄色 (2) の部分は +0.5 と +0.3 の間にあるため、別の変数関係が存在します。
0.8<a+b<1
a+b-(0.4-a)>0.8
a は緑色の部分の長さを表すため、不等式が成立します。
0<a<0.4
整理すると、
0.8<a+b<1
2a+b>1.2
0<a<0.4
次に、小数点以下の比較関係を分析すると、次の式が得られます。
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.5] → [0.3+(1-ab),0.3+(1-ab)+(0.4-a)]
即ち、
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.5] → [1.3-ab,1.7-2a-b]
したがって、小数点以下の範囲の縮小関係は次のように得られます。
(0.5-0.1) → (0.5-min(0.5-a,1.3-ab))
即ち、
0.4 → max(a,a+b-0.8)
2a+b=1.2のときの極値を求められるので、
b=1.2-2aとなり、
max(a,a+1.2-2a-0.8)
すなわち、
max(a,a+1.2-2a-0.8)
max(a,0.4-a)
a=0.2、b=0.8の場合、極値=0.2となります。
したがって、このケースでは小数点以下の範囲が最大 0.4 ~ 0.2 に制限できます。
2.
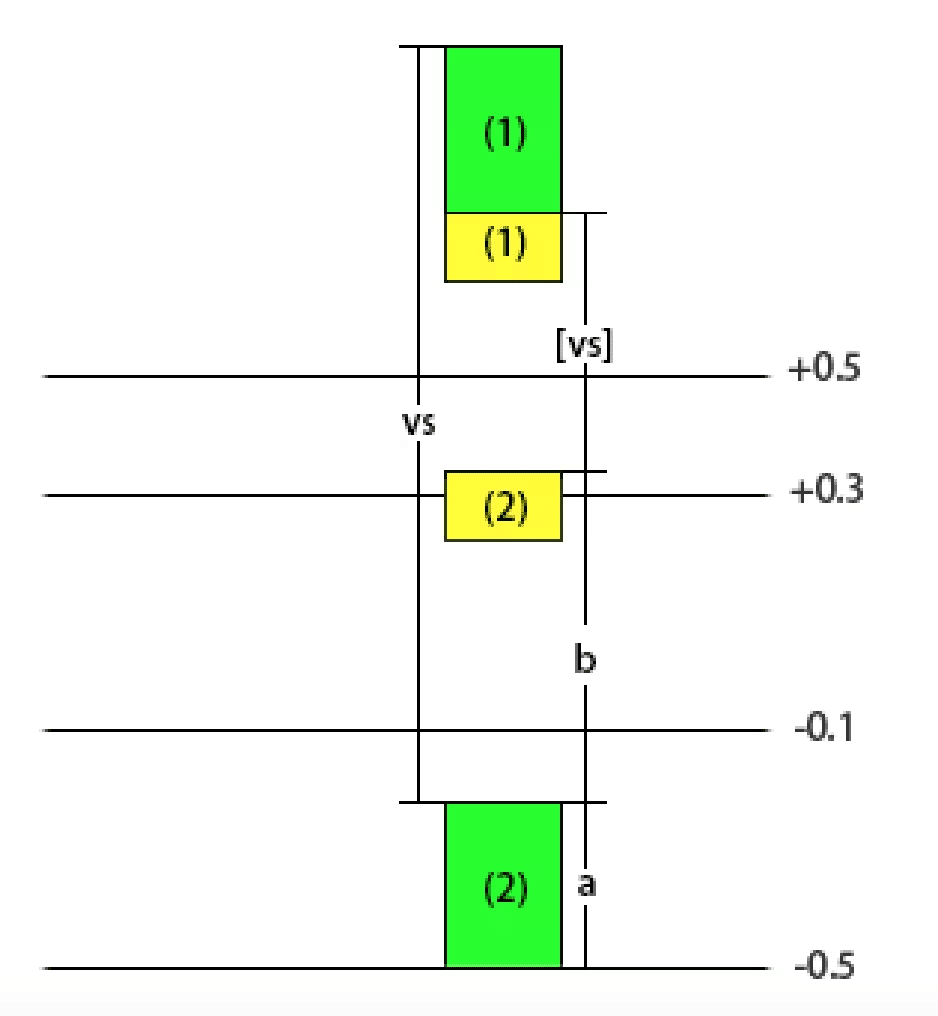
1の状況と比較すると、この状況との唯一の違いは、黄色 (2) が +0.3 制限の間にあることです。したがって、次のような不等式が成り立ちます。
a+b>0.8
a+b-(0.4-a)<0.8
即ち、
a+b>0.8
2a+b<1.2
元の制限 a+b<1、0<a<0.4 を追加すると、次のようになります。
0.8<a+b<1
2a+b<1.2
小数点以下の比較関係の計算を続けます。
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.1+a+(a+b-0.8)] → [0.5-(a+b-0.8),0.5]
[0.1+a+(a+b-0.8),0.5] → [0.1,0.1+(0.8-(2a+b-0.4))]
即ち、
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,2a+b-0.7] → [1.3-ab,0.5]
[2a+b-0.7,0.5] → [0.1,1.3-2a-b]
最初の2つの項から、小数点以下の範囲縮小関係を取得できます。
(2a+b-0.7-0.1) → (0.5-min(0.5-a,1.3-ab))
(2a+b-0.8) → max(a,a+b-0.8)
1.b<0.8
2a+b-0.8 → a
2a+b-0.8)/a に等しい範囲比は、
2+(b-0.8)/a
2は定数であり、b-0.8<=0 であるため、2 が最大値であることがわかります。したがって、b = 0.8のとき、aの値の範囲は0 - 0.2であり、2a -> aの漸化関係が与えられます。
離陸時の不確定範囲がどれだけ大きくても、現在の離陸時の不確定小数点以下の範囲を2倍にすることができるV-Stringが存在することが証明されています。
2.b>0.8
この場合、削減幅が2を超えないことを証明するのは簡単です。
3.

これは、黄色 (2) が +0.3 ~ -0.1 の場合です。
まず、a と b の値の範囲を分析します。
0.4<a+b<0.8
2a+b>0.8
次に、小数点以下の対応関係を分析します。
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.5] → [0.1+(0.8-ab),0.1+(0.8-ab)+(0.4-a)]
即ち、
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.5] → [0.9-ab,1.3-2a-b]
小数点以下の範囲縮小の関係は
(0.5-0.1) → (0.5-min(0.5-a,0.9-ab))
となり、
0.4 → max(a,a+b-0.4)
2a+b=0.8のときに極値が得られます。
b=0.8-2aを取得し代入して、
max(a,a+0.8-2a-0.4)
即ち、
max(a,0.4-a)
a=0.2の場合、最小値0.2が得られます。
したがって、この状況では小数点以下の範囲 0.4 が最大 0.2 の範囲にまで縮小できます。
4.

このケースは、黄色が-0.1の間にある場合です。
まず最初に、a と b の値の範囲を分析します。
a+b>0.4
2a+b<0.8
次に、小数点以下の比較関係を分析します。
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.1+a+a+b-0.4] → [0.5-(a+b-0.4),0.5]
[0.1+a+a+b-0.4,0.5] → [0.1,0.1+0.4-(2a+b-0.4)]
即ち、
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,2a+b-0.3] → [0.9-ab,0.5]
[2a+b-0.3,0.5] → [0.1,0.9-2a-b]
小数点以下の範囲の縮小との関係は次のとおりです。
2a+b-0.3-0.1 → (0.5-min(0.5-a,0.9-ab))
即ち、
2a+b-0.4 → max(a,a+b-0.4)
2. と同様であるため、ここではこれ以上分析しません。
5.

この場合、黄色 (2) の領域は -0.1 ~ -0.5 の範囲にあり、緑色 (2) の領域と重なっています。したがって、a と b の値の範囲には不等式があります。この状況から、b は負の数になる可能性があります。
0<a+b<0.4
2a+b>0.4
したがって、小数点以下の範囲間の対応関係は次のようになります。
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.5] → [0.1+(0.4-ab),0.1+(0.4-ab)+(0.4-a)]
即ち、
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.5] → [0.5-ab,0.9-2a-b]
小数点以下の範囲の縮小関係は、
(0.5-0.1) → (0.5-分(0.5-a,0.5-ab))
即ち、
0.4 → max(a,a+b)
2a+b=0.4のとき、極値は0.2みなされます。
したがって、この状況も0.4 から 0.2 の範囲にあります。
6.

この場合、黄色 (2)の部分が-0.5のラインを通り越しましたが、黄色(2)は+0.5に戻り、+0.3を超えません。
この場合、a と b の値の範囲は次のとおりです。
0<a+b<0.4
2a+b<0.4
小数点以下の範囲間の対応関係は次のとおりです。
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.1+a+a+b] → [0.5-ab,0.5]
[0.1+a+a+b,0.5] → [0.3,0.3-2a-b+0.4]
即ち、
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.1+2a+b] → [0.5-ab,0.5]
[0.1+2a+b,0.5] → [0.3,0.7-2a-b]
まず、最初の小数点以下の範囲縮小関係があります。
1個目:
(0.5-0.1) → (0.5-min(0.5-a,0.5-ab))
即ち、
0.4 → max(a,a+b)
2個目:
(0.5-0.1-a) → (0.5-min(0.3,0.5-ab))
即ち、
(0.4-a) → max(0.2,a+b)
3個目:
(0.1+2a+b-0.1) → (0.5-min(0.5-a,0.5-ab))
即ち、
(2a+b) → max(a,a+b)
これらは前の分析と同様なので、ここではこれ以上の分析は行いません。
7.

6とは異なり、+0.5 を下回る黄色 (2) ゾーンは +0.3 の制限を超えています。
a と b の制限的不等式は、
a+b>0
2a+b<0.2
小数点以下の範囲の比較関係は次のとおりです。
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.1+a+a+b] → [0.5-ab,0.5]
[0.1+a+a+b,0.3+a+a+b] → [0.3,0.5]
[0.3+a+a+b,0.5] → [0.1,0.1+(0.5-0.3-aab)]
整理すると、
[0.1,0.1+a] → [0.5-a,0.5]
[0.1+a,0.1+2a+b] → [0.5-ab,0.5]
[0.1+2a+b,0.3+2a+b] → [0.3,0.5]
[0.3+2a+b,0.5] → [0.1,0.3-2a-b]
したがって、次のようになります。
1個目:
(0.1+2a+b-0.1) → (0.5-min(0.5-a,0.5-ab))
(2a+b) → max(a,a+b)
2個目:
(0.3+2a+b-0.1-a) → (0.5-min(0.3,0.5-ab))
(0.2+a+b) → max(0.2,a+b)
3個目:
(0.3+2a+b-0.1) → (0.5-min(0.5-a,0.5-ab,0.3))
(0.2+2a+b) → max(a,a+b,0.2)
これらは前の分析と同様なので、ここではこれ以上の分析は行いません。
ケース6
これまでに行った5つのケースは全て、プレイヤーが -0.5 ~ +0.5 の範囲に居るとvspeedが0にリセットされるという初期値に基づいていますが、プレイヤーのvspeedが極端に小さい場合はこの仮定に当てはまりません。したがって、ケース6は、プレイヤーが着地したときのvspeedが非常に小さい (1 未満)の場合です。よく考えてみると、このケースは最初の5つのケースと同等であることがわかります。
簡単な証明をします。
プレイヤーが地面との距離 -0.5 ~ +0.5 でvspeedが0になっていない状態を状態Aとし、地面との距離 -0.5 ~ +0.5 でvspeedが0になった状態を状態Bとします。
1. 現在のプレイヤーのY座標 + vspeedがまだ地面に到達していないため、次のフレームはまだ状態Aにある。
2. 現在のプレイヤーのY座標 + vspeedが地面にぶつかるので、次のフレームは状態Bになる。
つまり、状態Aは必ず状態Bに収束することがわかるので、このケースは最初の5つのケースと同等です。
iii. 討議
上記の分析により、多くの圧縮方法があることがわかります。特に、不確定な範囲が半分に減少する可能性のある状況がいくつかあります。では、圧縮には制限があるのでしょうか? 小数点以下の範囲の 50% を圧縮できるV-Stringがあることは証明しましたが、このV-Stringを取得できるでしょうか?

この図は、より低い小数点以下の範囲に圧縮できるケースをまとめたものです。
これらのケースでは、プレイヤーは大きさxの小数点以下の範囲から最大max(a, x-a)まで圧縮できることがわかる。線を越えた場合、プレイヤーは0.3より後ろに落ち、その場合、より低い範囲に収束することは不可能です。 これらの場合、それぞれ、
1. vs-[vs]-(x-a)=0.8
2. vs-[vs]-(x-a)=0.4
3. vs-[vs]-(x-a)=0
となり、これらを照合すると、
vs-[vs]-(0.8または0.4または0)=x-a
となります。
vspeedは1フレームあたり0.4(重力)を加えるので、x.2xxxまたはx.6xxxを重力に重ねることで、x.0xxx、x.4xxxまたはx.8xxxの近くまで圧縮できます。 この圧縮の限界は、プレイヤーが得ることができるすべての vspeed のうち、x.0xxx、x.2xx、x.4xx、x.6xx、x.8xxより大きい最小の距離として求めることができます。
すべてのジャンプを列挙してみると、一段目の(3+2)カクタスが0.0075の最小距離を、二段目で(1+1+2)カクタスが0.003125の最小距離を取得でき、また蔦では、(4+1)カクタスで0.0005を得ることが出来ます。 ただし、これらの範囲に圧縮することに注意してください。
また、上記の着陸状況に入ることによってのみこれらの範囲に到達できるため、適切な V-Stringも必要です。 1段目ジャンプの場合、平らな地面では、V-Stringが(3+2)カクタスの理想的な着地を許さないので、平らな地面での1段目ジャンプでは、このような低い範囲にはなりません。地面が平らでない場合は、最低レンジの0.0075を得ることが可能です。 2段目ジャンプや蔦ジャンプの場合は、ジャンプ開始地点を自由に調整できるため、地面が平らでもその範囲を得ることが出来ます。
次に、1個のジャンプの50%圧縮の有無について分析してみましょう。
50%の圧縮率を達成するためには、a = x/2 とし、つまり、現時点で不確定な小数点以下の範囲の上限が着地時にちょうど(0.5-x/2)の位置に落ちる必要があります。もし、この対応する2段階のvspeedを得る方法が存在する場合、それによってプレイヤーがその位置に落ちる2段階のジャンプ開始地点が存在するはずです。したがって、問題は1段目のジャンプがその位置に到達できるかどうかに変わります。ジャンプの開始小数点以下(不確定な小数点以下の範囲の上限)も調整可能ですので、1段目のジャンプが目標の位置に到達できるように小数点以下を調整すればよいです。
プレイヤーの1段目のジャンプのY座標の密度を考慮すると、(0.4-x)の範囲内に達するのは非常に容易です。したがって、必要なvspeedが存在する場合、プレイヤーの不確定な小数点以下の範囲を半分に圧縮する方法が必ず存在します。したがって、0.2、0.1、0.05、0.025、0.0125、0.00625、0.003125の2段階のvspeedが存在する場合、プレイヤーは7 ~ 13回のジャンプで0.003125の小数点以下の範囲まで圧縮できます。ただし、残念ながら、このようなvspeedは存在しません。最もこれに近い2段階のvspeedのシーケンスは 0.2、0.1025、0.0515、0.0265、0.013475、0.0085、0.005375、0.003125 です。したがって、プレイヤーは平坦な地面で0.003125の小数点以下の範囲に調整するのに8 ~ 15回のジャンプが必要です。
iv. 結論
これで、すべてのケースが分析されましたが、章初めに記載した4フレームジャンプの性質は、ケース5の6の状況であることがわかります。
実際には、ここまで述べた内容は理論上の話なので、ゲーム上ではあまり有用ではありません。
例えば、離陸時の小数点以下の不確定の範囲がどれほど大きくても、 V-Stringは、現在のジャンプの不確定の範囲を2倍に減らすことができますが、プレイヤーの物理エンジンの制限により、一部のV-Stringが取得できないため、平坦な地面は最大でも小数点以下の範囲 0.003125 までしか圧縮できず、平坦な地面を考慮しない場合は 0.00075 になります。蔦を使用できる場合は 0.0005 になりますが、いずれにせよ、小数点以下の範囲を高い精度で圧縮するには、非常に回数の多いジャンプの行程が必要ですが、実際のところ、それを使う人は誰一人といません。
最後に、より実践的なことをいくつか紹介します。
4f→23f→23f→4f→1f→5f→5f→5f→5f→5f→23f→23f→6f
4f→23f→23f→4f→19f→23f→23f→6f
上記の 2 つのジャンプ方法では小数点以下を .425 ~ .5 の間に制限できますが、それが難しい場合、次の方法では小数点以下を .385 ~ .5 の間に制限できます。
4f→23f→23f→4f
これは、章初めに記載したFTFAの戦略にも使われています。
上記の .425 ~ .5 の範囲 (つまり、小数点以下の精度 0.075) は、平坦な地面でカクタスとジャンプキャンセル、2段ジャンプを使用せずに取得できる小数点以下の精度の最高値です。
17. 英語圏での技術の呼び名
横ドット
Align, X-Align, H-Align
縦ドット
subpixel, V-Align, Y-Align
(一部の海外勢はV-Stringと混同するため、subpixelを使用することを勧めています。)
ジャンプキャンセル
Jump Cancel, Cancel, JC
バニーホップ
Bunnyhop, bhop, bh
降りジャンバニーホップ
Bunnyfall, bfall, bf
A/Dトリック
A/D trick, A/D
ダイエット
HFPI, Diet
カクタス
Cactus
