有理数と無理数を繋ぐ方法(無理数の新しい計算方法)

2020年8月29日 19:37

「有理数と無理数を繋ぐ方法(無理数の新しい計算方法)」

👽：図_パスカル計算

山田：図_整数、虚数、無理数の関係と三角形関数

山田：この方法を使えば良いのか。

山田：無理数(円)と有理数(直線)の関係なの？

👽：
🔘👽°🍈🍈🍈🍈🍈1³pi/1³pi

4·(3/4)+4·(1/2)=
(12/4)+(4/2)=
(12/4)+(2/2)·(4/2)=
(12/4)+(8/4)=
(20/4)=(1/4)×20
→🍉🍉🍉🍉🍉
🍉🍉🍉🍉🍉
🍉🍉🍉🍉🍉
🍉🍉🍉🍉🍉 / (1)

→🍈🍈🍈🍈🍈 / (1)

👽：👽💜
(2)×(2/3)×(√a🐣)×(√a🐣)×(√a🐣)×pi

👽：図_パスカルの重ね(立体)計算

👽：(重ね)+(重ね)+(重ね)👽🔘

👽：図_パスカル量子化

👽：図_山田の図分解1

👽：図_山田の図分解2

👽：👽💜

山田：(2)×(2/3)×(√a🐣)×(√a🐣)×(√a🐣)×pi
これがわからない。。。🍉はわかる。。。なんで(2)×(2/3)なの？。。√🐣だから？、、次元を線に置いたから？
(※👽はこの質問にわかりやすく答えていませんが、暗に肯定しています)

👽：球体
空間に対する比率(4/3)😱
半球体(2/3)×(2)個

👽：球体
空間に対する比率(4/3)pi😱
半球体(2/3)pi×(2)個

👽：
(√0)³マグマ大使😱
(√1)³🍈
(√0)³ pi+(√1)³pi
🔘
(※空間に対する縦波と横波それぞれの関係を式化しています)

山田：空間内で、

・実回転(物理回転)と
・共鳴回転(内在倍音の回転)を

分ける必要があるんじゃない？もっとわかりやすくなると思うが。
(※(√0)³piや(√1)³piという表現が一般に分かりづらいと思ったため、一応言ってみたのですが、そもそも論を否定する結果となるため、却下します)

👽：図_空間での縦波と横波の関係

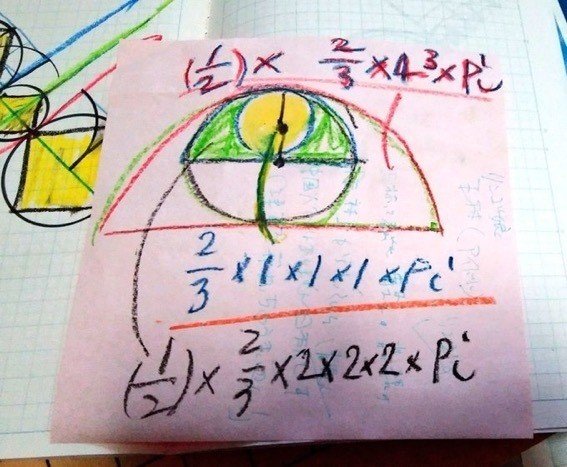
山田：そうか。回転を分けたらベクトル数が解離しちゃうね。却下。

<具体的な無理数の計算方法>

パスカルの定理で求めた解をこの図のように並べ換え、面を重複させ加算します。