
【保存版】ECDSAを理解するために!(離散対数問題/楕円曲線上の離散対数問題)
こんにちは、CryptoGamesの高橋です。
TCGVerseの会社です。
本日、TCGVerse構想を発表いたしました!https://t.co/1zeMA2VbH4 pic.twitter.com/FIOXwADoEc
— 小澤孝太@CryptoSpells / CryptoGames CEO (@kotaozawa) December 28, 2021
ECDSAについての理解を深めるために、離散対数問題、楕円曲線の離散対数問題について学んだのでアウトプットしていきます。
なお、参考にさせていただいた記事は一番下に載せていきます。
0 前提知識
0ー1 p:素数
素数は英語で「Prime number」なので、よくpとして出てきます。
この記事でも素数はpで表していきます。
0ー2 mod : モジュラ演算
割った余りを求める計算がモジュラ演算です。(参考記事:https://pebble8888.hatenablog.com/entry/2017/06/10/231249 以下、しばらく同じ)

1ー1 原子根とは
下のように、例えば、13という素数である数の乗数を割っていった時に、余り1が出ないものが原子根です。
(図を見ていただいた方がわかりやすいと思います。)

ちなみに、無限に計算した結果、余り1が出ないというものではないです。
今回の場合上の例のように、p -2乗である11乗までを行います。
1ー2 原子根のポイント ①重複しない
これがとても大事だと思います。
下のように右の10から始まるmodの結果は重複しておりません。
そのため、乗数と結果が1対1の関係になっています!

1ー3 原子根のポイント ②規則性がない
また、下のように規則性もありません。
これにより、規則的に結果を導くことができず、計算を行わなければ結果が導かれません。

2ー1 離散対数問題とは
では、これを踏まえて下のように見てみましょう。
6の「3」乗の結果を求めるには一つ計算すれば良いので簡単に求めることができます。

一方、余りが4になるための乗数を求めるのはどうでしょう。
1対1の関係なので、必ず答えはあります。
でも規則性はないので一つ一つ計算して答えに辿り着くしかありません。これは大変そうですね。
この右辺から左辺方向の計算が離散対数問題です。
2ー2 離散対数問題はどうなると難易度が上がる?
上の例では、13で割っていました。
その結果、右は2から12の11パターンが存在しました。

ということはこの割る数字を大きくすれば難易度が上がりそうですね。
2ー3 どこが間違っていますか?
では、割る数を100にしたらどうでしょう??
これは正しくありません。
どこが違うでしょうか??
2ー4 割る数は素数にしましょう。
割る数は素数でしたね。

そのため、101などの素数を使うと101-2の99通りとなり、上の13の時の例よりも難易度が上がります。
このように素数pを大きくすることで難易度が上がっていきます。
2ー5 原子根も見てみましょう。
こちらのサイトに500以下の素数の原子根が載っていました。
https://blog.thetheorier.com/entry/primitiveroot-list

このように素数101の原始根は40個あるようです。
そのため、例えば原子根99を使って
「99をr乗して、101で割った余りが70になるようなrを求めよ」
というような離散対数問題も作れそうですね。
2ー6 離散対数問題が直接暗号に使える?
ここまで見てきました離散対数問題は特定の条件下では、比較的簡単に解けてしまうようです。
そのため、実用化されているのが楕円曲線上の離散対数問題のようです。
では、そちらも見ていきましょう。
3ー1 楕円曲線について
まずは、楕円曲線について一つずつ学んでいきましょう。
楕円曲線の一般式は下のようになります。(参考記事:https://zoom-blc.com/what-is-ecdsa)
y^2 = x^3 + ax + b

そして、イーサリアムなどで用いられるsecp256k1曲線はa=0,b=7なので、下のようになります。
y^2 = x^3 + 7
3ー2 secp256k1とは
楕円曲線暗号を使うには、上のa,bの値や後から出てくるスタート位置などのパラメータの指定が必要です。
なお、
secp112r1, secp112r2, secp128r1,,,,
のようにいろいろな設定されているパラメータのセットがある中、イーサリアムではsecp256k1というパラメータ群を用いています。
3ー3 楕円曲線上での加算
楕円曲線上での加算は下のように定義されています。

AとBを結んだ直線と楕円曲線が交わったところのx軸に関する対称点です。
言葉の説明より、見た方がわかりやすいと思います。
G + Gのように同じ場合は接線になります。

そして、G + G=2Gで表せます。
3ー4 (練習)3Gを求めてみよう
同じ要領で3Gも求めてみましょう。(例としての最初のGの位置を変えました。)

こんな感じになるのですが、イメージはあっていましたか?
3ー5 tGについて(よく、nで表しますが、位数と区別するためにtとしました)
3ー4はGを3つ足したものでした。(G + G + G)
このようにt個加算した場所はtGで表されます。
3ー4の場合は3Gですね。
3ー6 Gの値は?
この例ではGの場所はわかりやすい場所にありますが、実際にはGの値はsecp256k1で定められています。(3ー2参照)
Gのx座標は
0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f8179
Gのy座標は
0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
となります。
とても大きい数ですね。
4ー1 無限遠点について
まずは無限遠点についてです。(参考記事:https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11210553716)

無限遠点とは平行線が限りなく遠いところで交わる点のようです。
その、限りなく遠いところは無限遠と言われているようです。
4ー2 楕円曲線における無限遠点とは
楕円曲線における無限遠点は、楕円曲線上の点ではないようです。
y軸に平行な直線と無限に遠くにある交点のようです。

4ー3 無限遠点の使い方
P+Q=0となります。
Oは無限遠点を表します。(楕円曲線の加算について不明になってしまった場合は3ー3をご参照ください。)
下の図はただのイメージですが、このように、PとQがy軸に平行に近づけば近づくほど、交点はずっと遠くなります。

これがPとQでy軸と平行になれば、無限遠点で交わることとなります。

4ー4 P + O(無限遠点)について
P + O(無限遠点)は下の図のようにPになります。(P + 0 = P)

楕円曲線の加算の通り、PとOの直線と楕円曲線の交わった点についてのx軸に関する対称点でしたね。(3−3参考)
5 単位元について
単位元についての説明です。
単位元とは、下のように、演算しても、元の値をそのまま返す値です。

そのため、足し算の場合は0、掛け算の場合は1になります。
例
足し算 10 + 0(単位元) = 10 (元の10が返ってきた)
掛け算 10 × 1(単位元) = 10 (元の10が返ってきた)
4ー4でP + O(無限遠点) = P と求めたように、O(無限遠点)は単位元であることがわかりました。
6ー1 位数について
下にあるように、位数とは、何回演算したら単位元になるかという数値のようです。

楕円曲線において、単位元とは0(無限遠点)でした。
つまり、G + G + G + .....を何回繰り返せば0(無限遠点)になるのかの回数が位数となります。
6ー2 楕円曲線における位数について
3ー5で扱ったように、Gをt個加算した場所はtGで表します。
よって、n個加算して無限遠点と交わる場合は
nG = 0(無限遠点)
となります。
n回演算すれば、単位元である0(無限遠点)になるので、このnが位数となります。
ちなみに、この位数のnはsecp256k1でパラメータとして定められており、10進数にすると
115792089237316195423570985008687907852837564279074904382605163141518161494337
といった、かなり大きな数字になります。
Gを上の途方もない回数加算すると0(無限遠点)と交わります。
7 Gを生成元とする巡回群
6ー2で導かれたnG = 0から
(n + 1)G = G
が導かれます。
(参考)
左辺を展開すると、nG + G となり、nG = O のため、G + Oとなる。
5ー4から、G + O = Gが導かれる
つまり、n+1番目にGに戻っていきます!
無限遠点の次がGなのですね。
そのため
{G, 2G, 3G, ,,,,,,,, nG}を一括りとして、循環しています。
ちなみに、2G = G + G のように、全てがGという要素で構成されていました。
このようなまとまり(群)をGを生成元とする巡回群と言います。
8 楕円曲線上での有限体演算
今まで、実際に座標上にある実数で考えてきました。
これを実数体と言います。
一方、楕円曲線暗号では、有限体(ガロア体)で楕円曲線を考えます。
9ー1 有限体(ガロア体)とは
有限体(ガロア体)とは位数が有限である体の事のようです。

secp256k1では、非常に大きいながらも位数は有限でしたね。(6ー2参照)
そして、有限体は英語で「Finite field」なので、位数がqである有限体はFqなどと表します。
9ー2 有限体の四則演算は?
有限体のポイントは四則演算(足し算・引き算・掛け算・割り算)だと思います。
通常の四則演算とは異なるルールがあります。

それは最後に位数である2で割った余りが解となることです。
例えば
1 + 1 = 2 ⇨ 2 mod 2 = 0
1 × 0 = 0 ⇨ 0 mod 2 = 0
のような感じです。(modは1ー1参照)
この辺り、どこかで見たと思ったら、1ー4でやった、離散対数問題と考え方がとても似ていますね。
9ー3 具体例で考えよう
次のように位数が43である有限体を考えます。
yが12の時、通常の計算であればy^2 = 12^2 = 144になるはずです。

しかし、今回の四則演算は、その結果は43で割った余りなので、
y^2 = 12^2 = 144 mod 43 = 15となります。(144を43で割った余りが15)
つまり、左辺の解は144ではなく、15です。
一方、x =2の時、x^3 + 7 = 2^3 + 7 = 15で、左辺と右辺が一致します。
よって、(x, y) = (2, 12)の時に方程式を満たし、この点を「有理点」と言います。
そして、普通に計算すると、
左辺 12^2 = 144
右辺 2^3 + 7 = 15
で左辺と右辺は一致しません。
このように楕円曲線上にない点であるということもわかりました。
10 楕円の離散対数問題について
10ー1 準備 まずは実数で考えてみる
Gを3回加算した時(3G)下のようにXに到達したとします。(不明な場合は3ー3をご参照ください。)
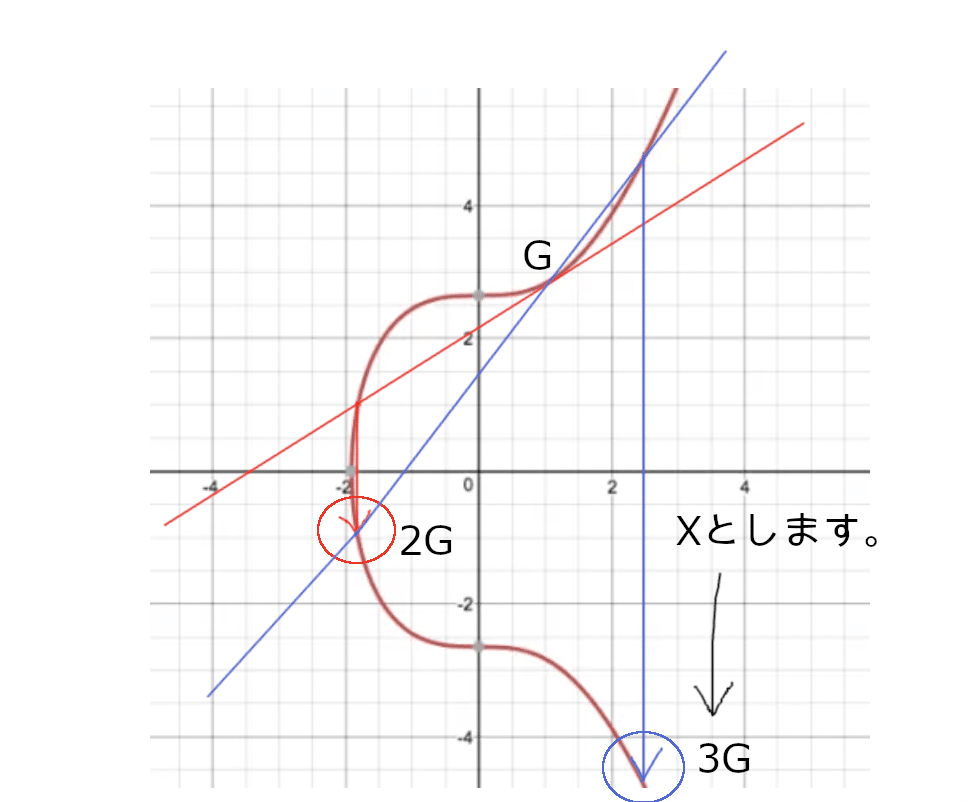
式としては、
X = 3G(Gを3回加えた)
となります。
この場合、「3」いう数字が与えられた時、Xを求めるのは、ただ計算すれば良いので簡単そうです。
一方、Xに辿り着くにはGを何回加えたか(何倍したか)という解を求めるのは難しそうですね。

10ー2 離散対数問題と比較
では、離散対数問題を思い出してみましょう。

離散対数問題では、例えば
・6の3乗を13で割った余りの計算 ⇨ 簡単
・6を何乗して13で割れば4になるか ⇨ 難しい(離散対数問題)
というように、何乗かというべき乗を求めたのに対して、楕円曲線の離散対数曲線は何倍かという倍数を求めることになります。
このように
・離散対数問題 ⇨ 何乗かを求める
・楕円曲線の離散対数問題 ⇨ 何倍かを求める
との違いがありました。
10ー3 modは?
最後にmodです(割った余り)
離散対数問題は割った余りである、modを使うことによって、計算を複雑にしていました。
10ー1の段階ではmodが使われておりません。
そのため、実際の楕円曲線暗号では、9章で取り上げた有限体が使われます。(9ー3の具体例参照)
これにより、四則演算の際にmodを計算に取り込んでおります。
以上が離散対数問題、楕円曲線上の離散対数問題でした。
ちなみに、以下、参考にした記事です。
いいなと思ったら応援しよう!

