
【完全保存版】ビットコインの難易度(ディフィカルティ)を具体的な値で考えよう
0 はじめに
本日は、ビットコインの難易度(ディフィカルティ)が結局なんなのかについて、学んでいきたいと思います。
1 例から考える
まずは簡単な例で考えてみましょう。
「1から100の数字のうち、70以下の数字を選ぶ確率」はいくつでしょう。(それぞれの出る確率は同じだとします。)
それは、下のように、「70 / 100」となりますね。

一方、10以下の数字を選ぶ確率は「10 / 100」となります。
ビットコインのディフィカルティでは、この「分子」を操作します。
分子の値は「ターゲット」と呼ばれます。

2 ビットコインのケースで考える
なお、実際のビットコインで考える場合、難しそうなポイントは下の2点です。
① 値が16進数である
② 値がすごく大きい
1 分母を求めよう
まず、分母の数を考えてみましょう。
先ほどの例で言うと、100の部分です。
まず、今回使用する値は、下のように、64個のランダムな値が並んでいます。

なお、この辺りは実際にやってみる方がしっくりくると思います。
と言うことは、16の64乗通りの値が考えられます。

2 2のべき乗に直してみよう
そして、よく見る、2のべき乗の書き方に直してみましょう。
ここは数学の復習です。
下のように2の256乗になります。

このようになりました。

3 分子(ターゲット)を求めよう
次に、当たりとなる「ターゲット」を求めましょう。
先ほどで言うと、「70 以下の数値」の70がそれに該当します。
これは、「最大ターゲット値」と「デフィカルティ」から求まります。

4 最大ターゲット値について
そして、「最大ターゲット値は」こちらの値になります。
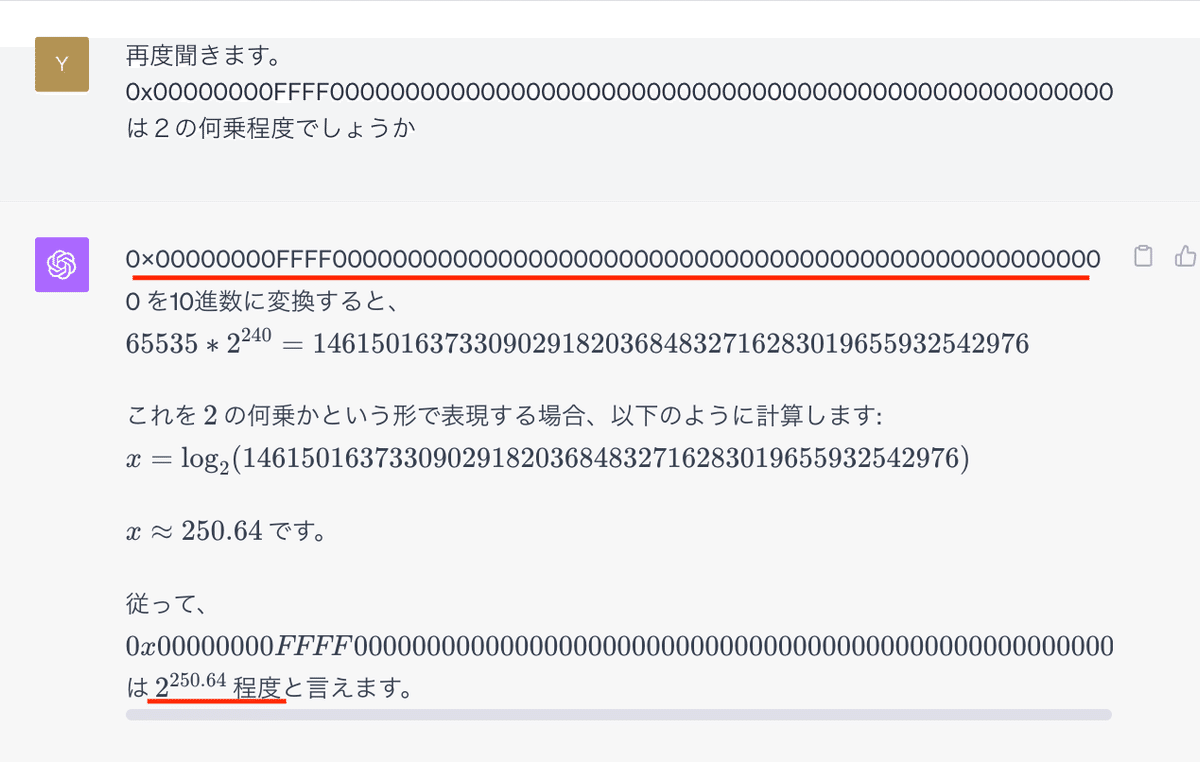
「0x00000000FFFF0000000000000000000000000000000000000000000000000000」

16進数ではよくわからないので、10進数に変えてみましょう。
おおよそ、2の250.64程度のようです。
5 難易度:1の場合を考えよう
そして、この、最大ターゲット値をディフィカルティで割った値がターゲット値です。
このターゲット値が「70 以下の数値を見つける」などの「70」の部分に相当します。

そのため、下のようになります。
大きすぎてわかりにくいですが、ディフィカルティが1の場合は、「約2の250.64乗という数値」以下の値を見つけることになります。

6 現在の難易度(約58兆)で考えよう
その時点での難易度はこの辺りで確認できます。
今回は、難易度58兆として考えてみましょう。

では、こちらの計算方法に基づいて計算してみましょう。

下のように、2の34.54乗程度になるようです。

つまり、このようになりました。

以上です。
いいなと思ったら応援しよう!

