【補足】連続するオイラー素数の積が存在する理由

以下の記事を読み、興味のある方のみご覧ください。

上記記事で書いた内容の補足です。ちょっとした性質の証明について書いております。

f(n) = n^2 + n + 41

というオイラーの素数生成多項式があり、nに0から順番に代入すると素数になります(この素数のことを「オイラー素数」といいます)。

f(0)=41
f(1)=43
f(2)=47
f(3)=53
f(4)=61
f(5)=71
f(6)=83
f(7)=97
f(8)=113
f(9)=131
f(10)=151
︙

n=39まではすべて素数になりますが、n=40で初めて素数ではなくなります。

(これが「その時」の瞬間でした笑)

さて、素数でないものをいくつかピックアップしてみると、以下のようになっています。

n=40, f(40)=1681=41×41
n=41, f(41)=1763=41×43
n=44, f(44)=2021=43×47
n=49, f(49)=2491=47×53
n=56, f(56)=3233=53×61
n=65, f(65)=4331=61×71
n=76, f(76)=5893=71×83
n=89, f(89)=8051=83×97

素因数に注目すると、連続するオイラー素数たちのかけざんで表されているのです！

f(0)=41
f(1)=43
f(2)=47
f(3)=53
f(4)=61
f(5)=71
f(6)=83
f(7)=97

実は、これは偶然ではありません。オイラーの素数生成多項式において、以下のようなことが成り立ちます！

例えば、

f(0)=41
f(1)=43

となりますが、両方の値を平均して1引くと、

(41+43)/2 − 1 = 41

ここで得られた41を素数生成多項式に代入すると、

f(41)=1763=41×43=f(0)×f(1)

となっているのです。

いくつかのケースを調べてみると、この法則に気がつくことができます。これを一般化して証明してみました。

以下、画像で載せておきます。ゴリゴリの計算をするだけですけどね…笑。

(細かい計算は省いています)

ということで、

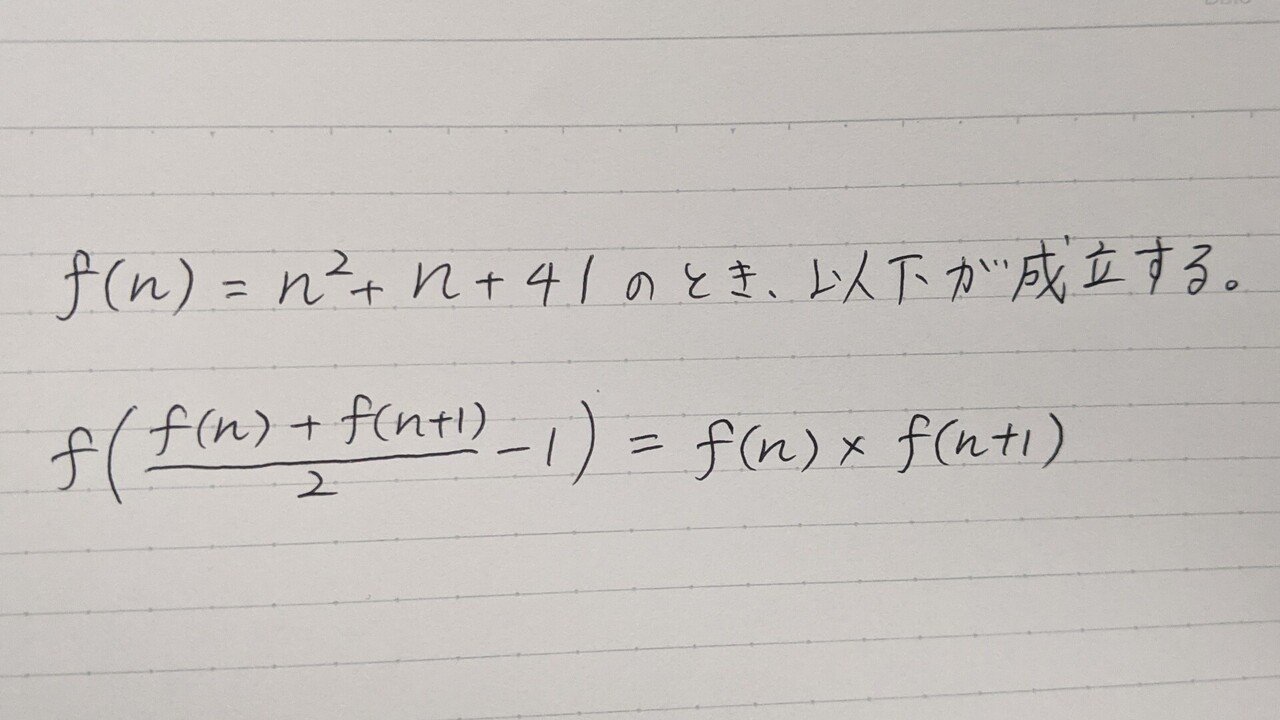
が成立するのです。

いかがでしたか？

連続するオイラー素数のかけざんの値が、オイラーの素数生成多項式の中に必ず存在します。なかなか面白い性質だなと思いました。

素因数分解を速攻でこなしたい人間としては、今回登場したオイラー素数たちのかけざんは覚えておきたいものです。ゲーム「Prime Smash !」でも役に立ちそうですし…笑。

f(40)=1681=41×41
f(41)=1763=41×43
f(44)=2021=43×47
f(49)=2491=47×53
f(56)=3233=53×61
f(65)=4331=61×71
f(76)=5893=71×83
f(89)=8051=83×97

興味がある方は、上記の素因数分解を覚えてみてください！

素数はいつも、あなたのそばに。
Let's enjoy SOSU !

最後まで読んでいただき、ありがとうございました。