
【素数探し】エラトステネスの篩で素数を見つけよう!
皆さんは、「エラトステネスの篩」というものを知っていますか?
エラトステネスは、紀元前の古代ギリシアの科学者です。
エラトステネスの篩とは、簡単にいうと、
素数を見つけるための方法
です。原始的な方法で、そんなに難しくありません。数学が苦手な方でも素数と親しむことができます。
そこで今回は、「エラトステネスの篩」のやり方を解説します。なるべく丁寧に説明しますので、最後まで読んでいただけると嬉しいです。
それでは、始めます。
【一応念のため】
素数とは、1と自分自身以外で割れない数のこと
もしくは、約数が1と自分自身の2つしかない数のこと
ここでは、100以下の素数を求めていきます。
一つ求めておきたいのが、100の平方根。これは、√100 = 10 となりますね。この数まで、以下のような操作を続けます。
数字をまず書き出します。今回の例では100までの数字を列挙しています。ここでは詳しく説明しませんが、1は素数ではないので省略しています。
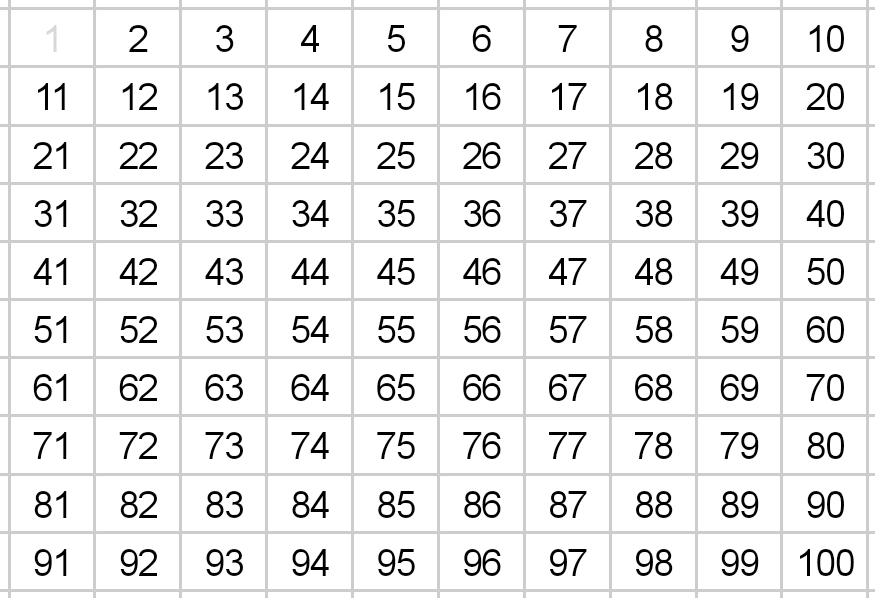
まず、先頭の「2」に注目し、2以降の2の倍数をチェックしていきます。紙でやる方は、数字の上にバツを書いていけば良いです。
4, 6, 8, 10, ... , 98, 100
とチェックできますね。
↓画像の黄色で塗られた部分が2の倍数です

今チェックした数たちは、素数ではありません。なぜなら2で割れてしまうから。
こうしてまず、2以外の偶数がなくなりました。

(赤数字は素数であることが確定した数)
次に、2の次の数である「3」に注目。今度は、3の倍数をチェックしていきます。既に消えている所は無視しても大丈夫です。
9, 15, 21, 27, ... , 93, 99
を新たにチェックできましたね。
↓画像の黄色で塗られた部分が3の倍数です

これらも素数ではありません。よって、同じように削除します。

以降同様に、5の倍数や7の倍数についても同じことをします。
5の倍数をチェック↓

それらは素数ではない↓

7の倍数をチェック↓

それらは素数ではない↓

11の倍数はチェックしなくて大丈夫です。先程、100の平方根の10を求めましたが、10以下の数字について調べれば十分なのです。
よって、残った数が100以下の素数となります。

もっと大きい数について調べたい場合は、11や13などの倍数についてもチェックする必要があります。
ただ、覚えておいてほしいのが、
n以下の素数を知りたい場合は、√n 以下の倍数をチェックすれば良いということです。√n 以下の倍数をチェックしていれば、それより大きい倍数のものはすでにチェックされているのです。
例えば、100以下の素数を知りたいとき。7の倍数まではチェックできているとしましょう。
もし11の倍数をチェックするのであれば、
11×2, 11×3, 11×4, ...
とチェックしていくわけですが、これらの数は前の段階でチェック済なのです。
(11×2は2の倍数で、11×3は3の倍数のところでチェックしているはず!)
となると、チェックされていない数で最小のものは、11×11となるわけですが、これは121なので100よりも大きくなってしまうのです。
ざっくりとした説明ですが、何となくお分かりいただけたでしょうか?とにかく、「平方根以下の倍数だけをチェックすれば良い」と覚えておけば大丈夫です。
いかがでしたか?
エラトステネスの篩は良い計算練習になるとともに、頭の体操にもなります。
そして、素数を自分で発見できる貴重な機会になるのです!ぜひとも、素数を好きになるきっかけとして「エラトステネスの篩」をご活用ください!
素数はいつも、あなたのそばに。
Let's enjoy SOSU !
最後まで読んでいただき、ありがとうございました。
