【塗り数字-19】Let's make SOSU !
今回は、塗り数字の第19弾！数字を塗って素数を作るゲームです。
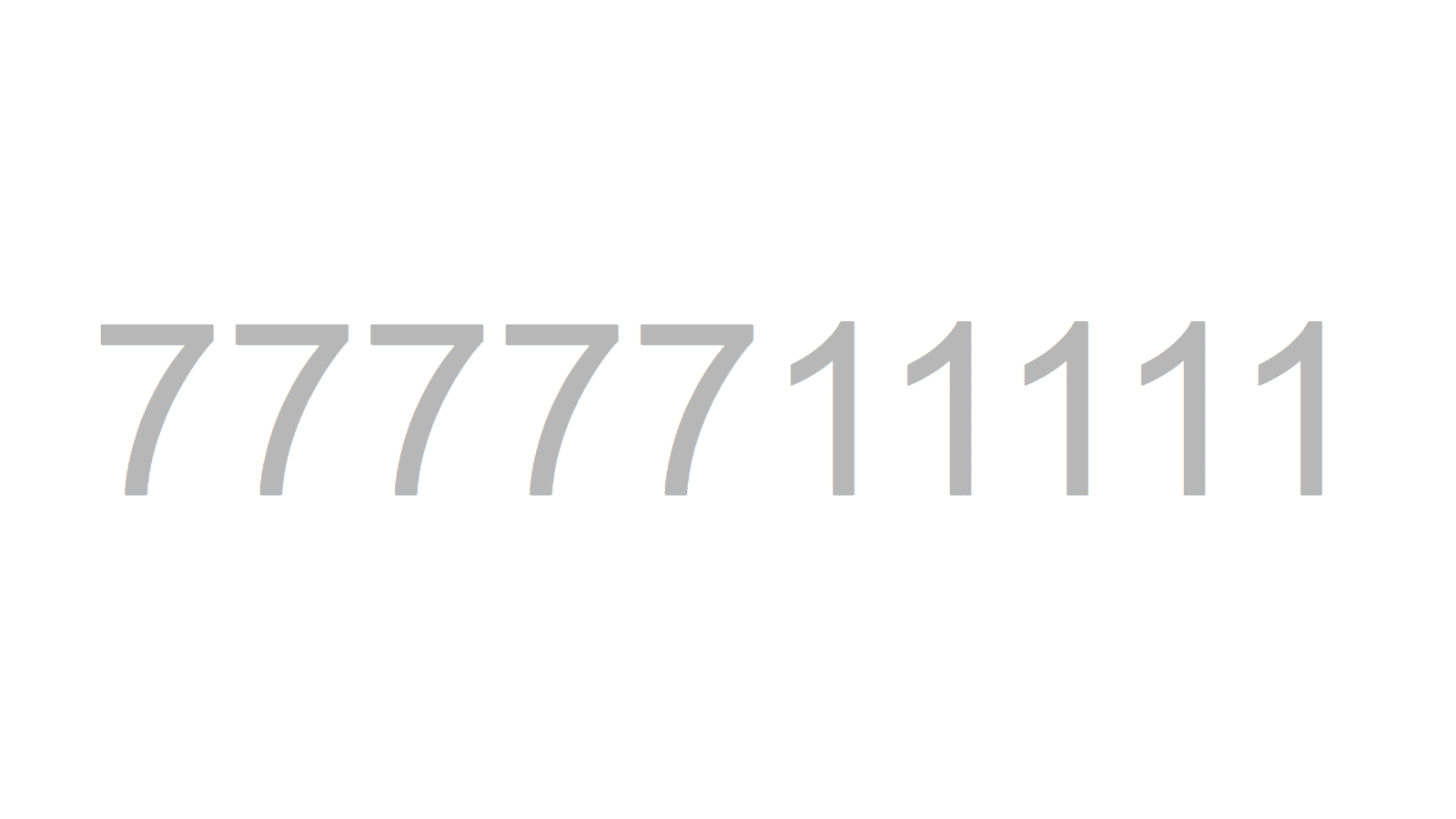今回は前回と逆で、7が5個並んだ後に1が5個付いています。果たして、この中に素数はどれくらいあるのでしょうか…？
一桁だと、7が素数ですね。2桁以上の素数がどれくらいあるのか、考えてみてください！
まずは2桁。もう何度も紹介していますが、11を4通りで塗ることができます。
11はレピュニット素数という名前が付いていましたね。
他の二桁の素数は71だけ。数字をひっくり返した17も素数ですね。このような素数は「エマープ」と呼ばれています。
3桁や4桁の素数は無く、次は5桁。前回も描きましたが、7と1の個数比が大事ですね。4:2や6:3など、両方の数字の最大公約数が2以上になる場合は、何かしらの数で割れてしまいますね。
最大の素数は、8桁の77711111です。7と1の個数比は3:5になっていますね。
最後に、惜しくも素数ではない合成数の素因数分解を紹介します。
7111=13×547
7771=19×409
71111=17×47×89
77111=29×2659
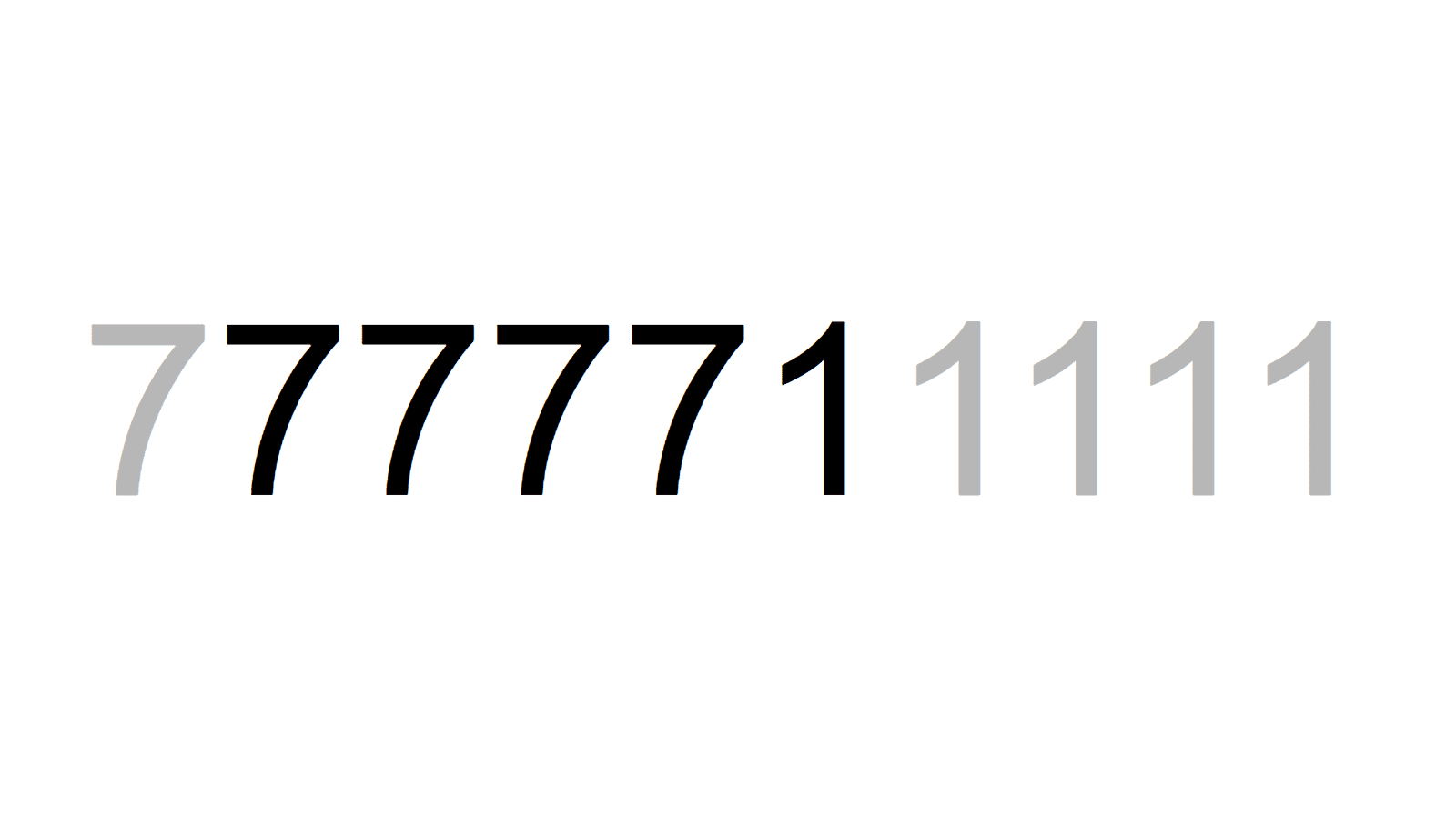77771=83×937
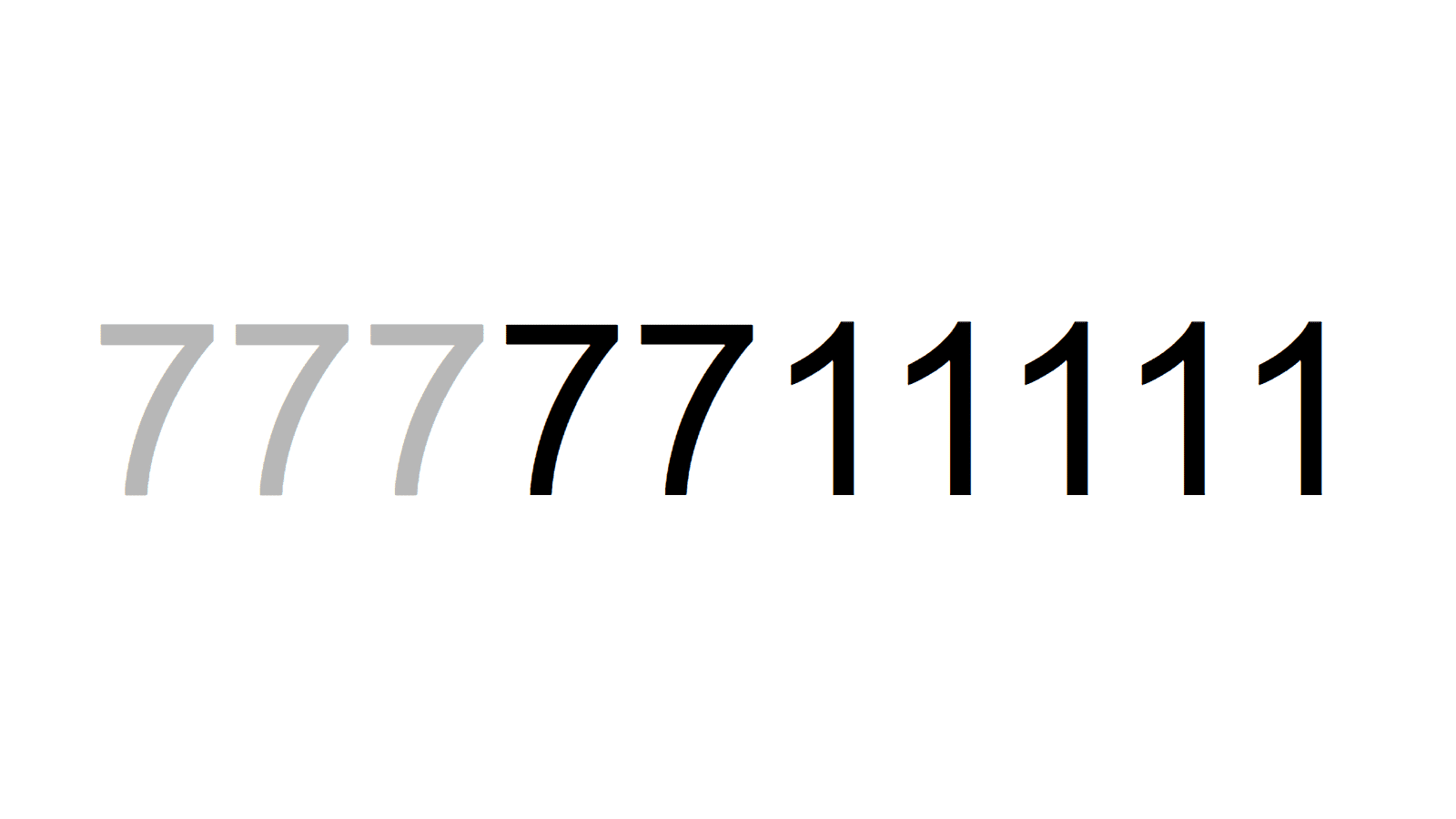7711111=79×97609
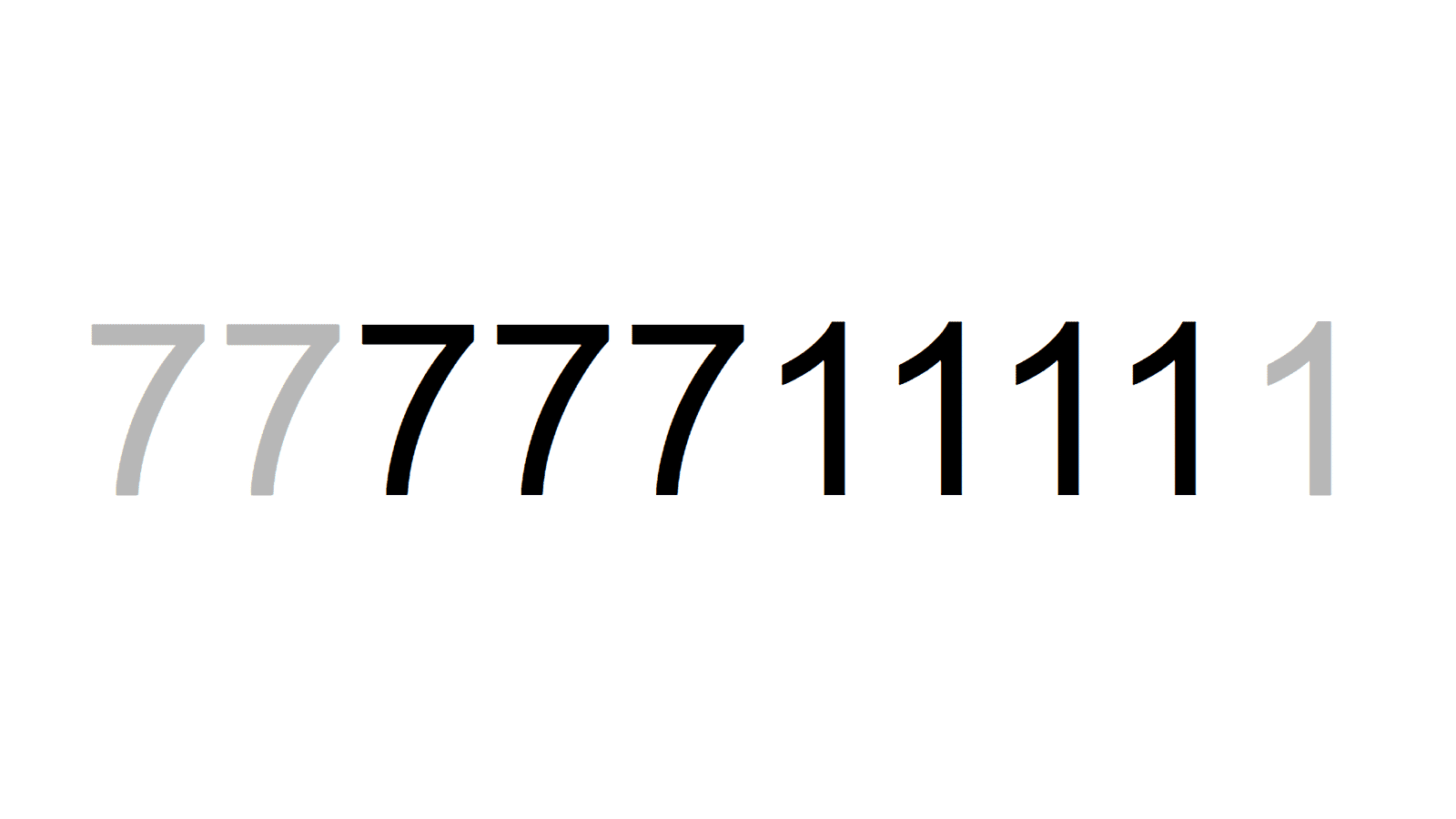7771111=31×250681
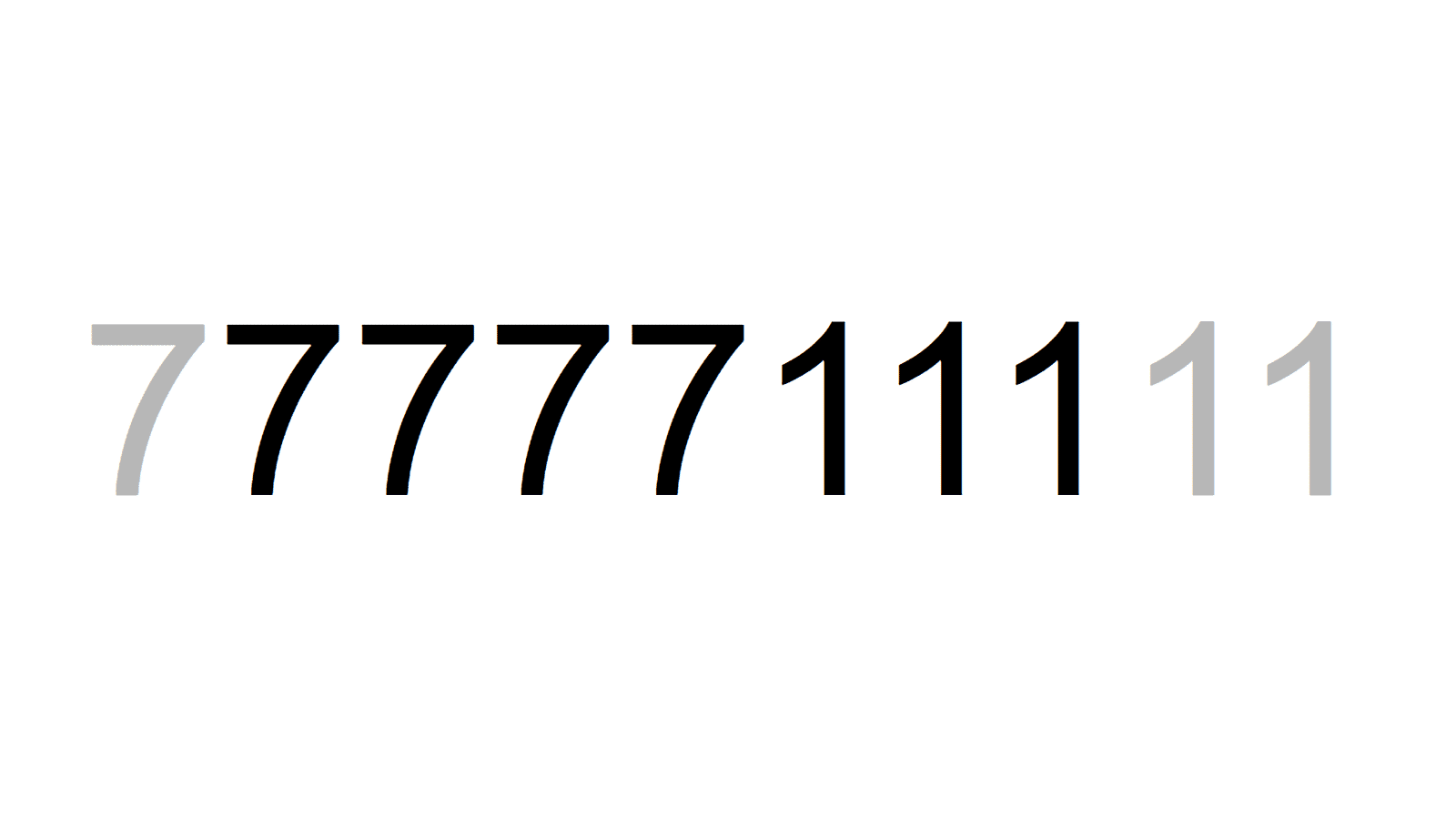7777111=313×24847
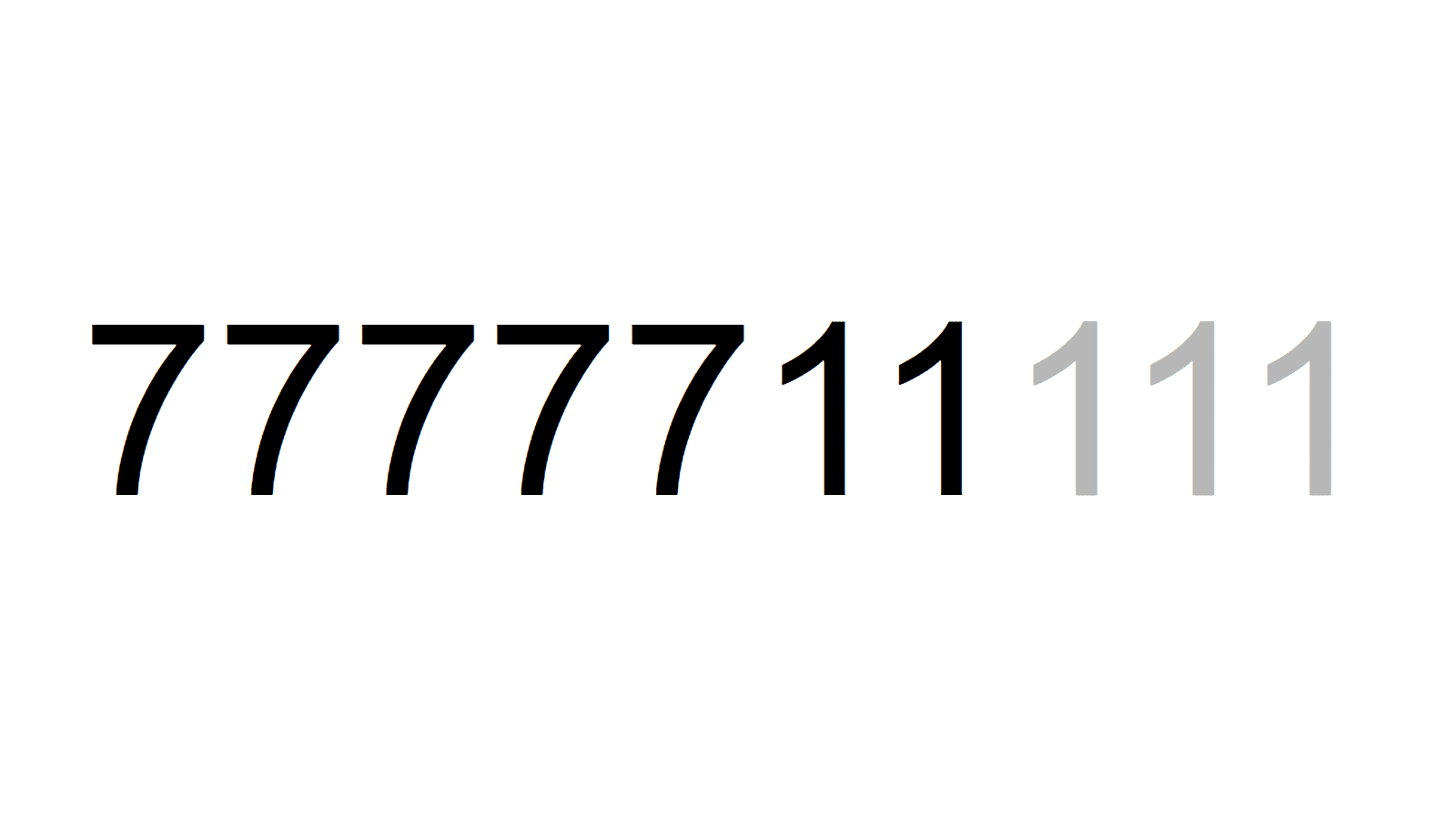7777711=43×191×947
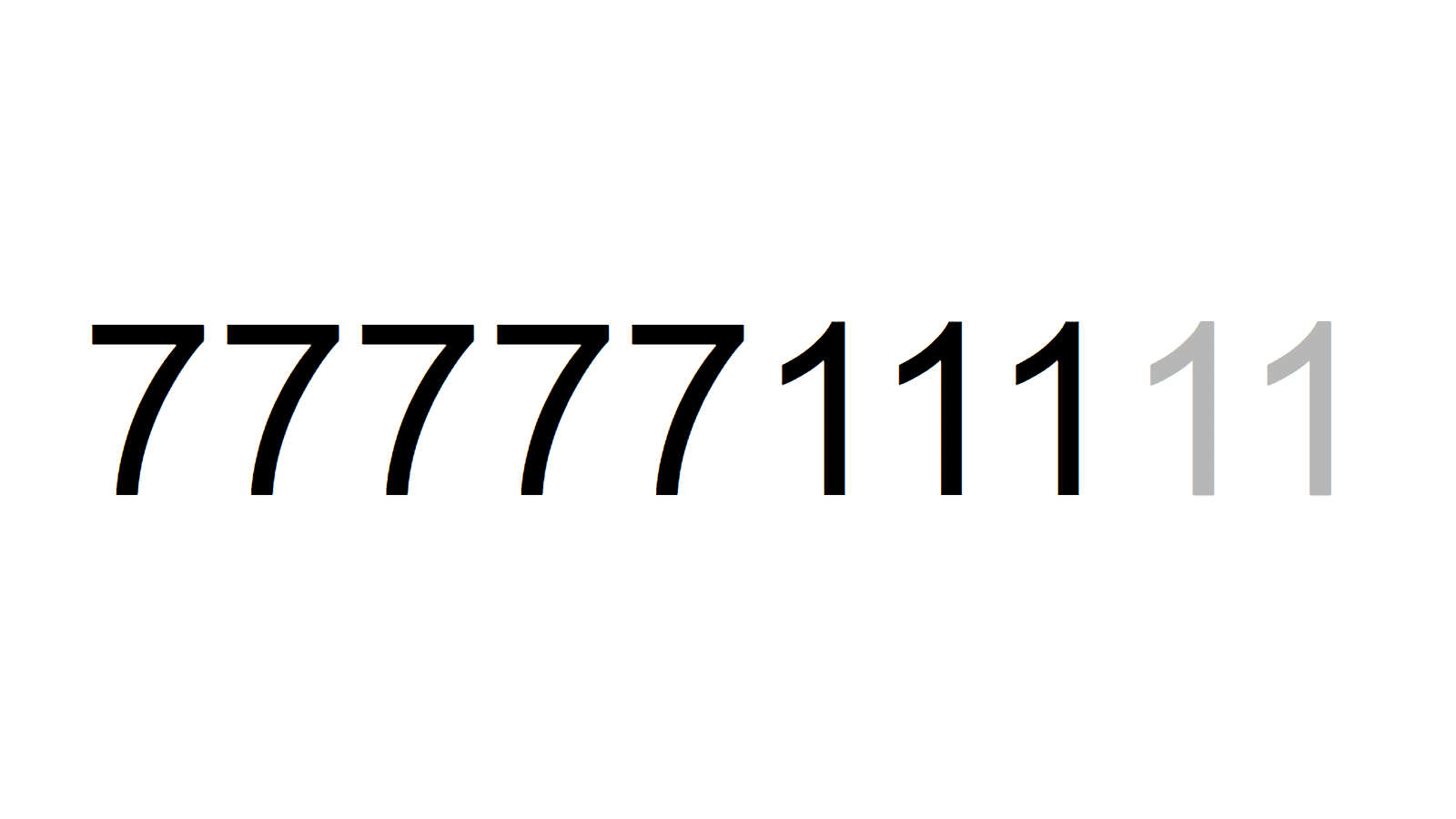77777111=179×434509
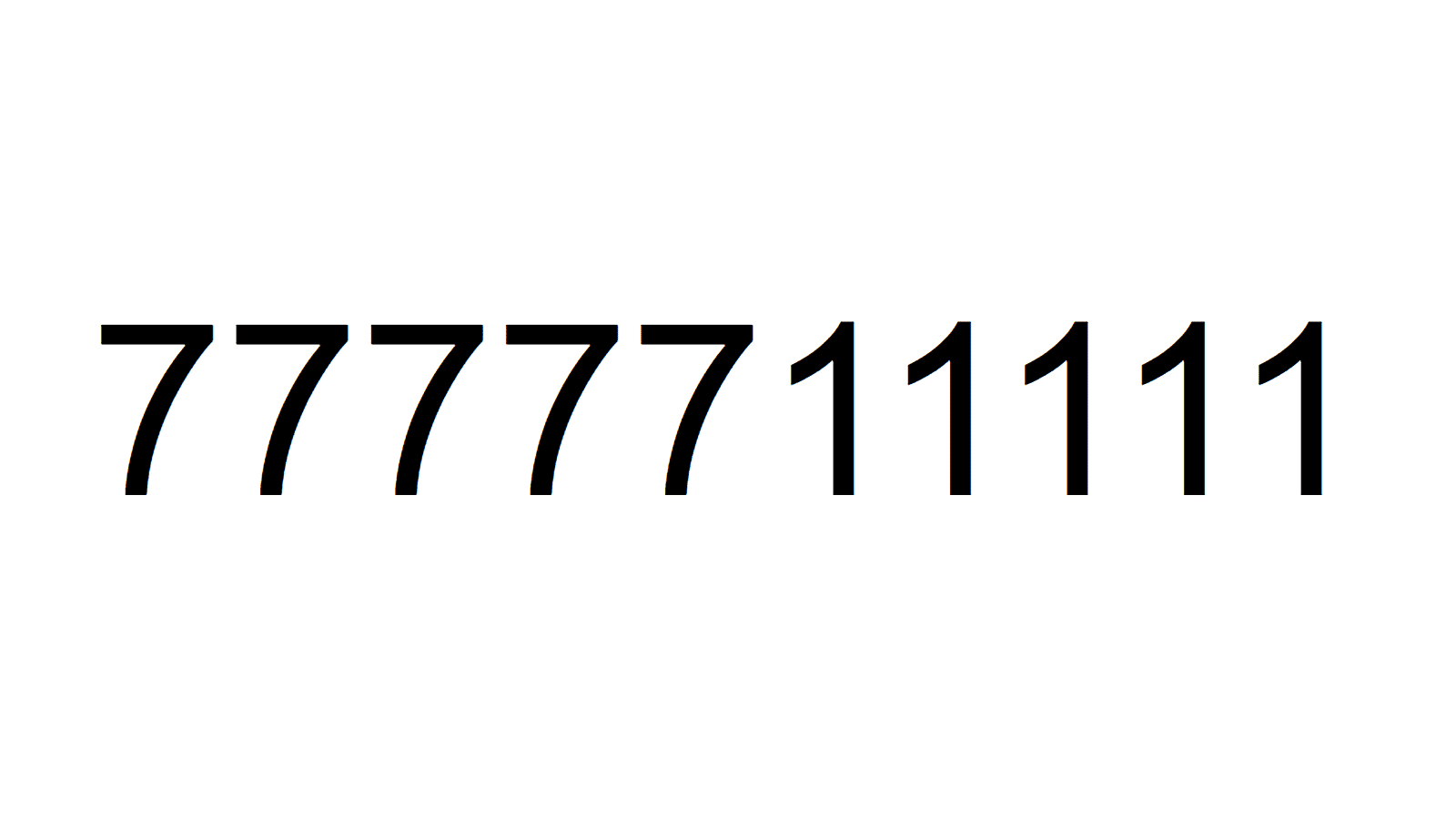7777711111=41×271×700001この記事が気に入ったらサポートをしてみませんか？