
【Lucky!】良いことがある!?「幸運数」とは
世の中には「〇〇数」と呼ばれるものがたくさんあります。知らないものもたくさんありますが、面白い数があれば紹介したいなと思っています。
今回は、「幸運数」という数について説明します。いかにも良いことがありそうな素敵な数ですが、果たしてどんな数なのか…?
昨日は「エラトステネスの篩」を紹介しましたが、実は「幸運数」の求め方は「エラトステネスの篩」と似ているのです。
もし「エラトステネスの篩」を知らない方は、先に読んでおくことをおすすめします。
方法がやや複雑ですが、なるべくわかりやすく説明していきたいと思います。尚、小さい順に並んだ数字の列のことを「数列」と書いています。
(説明でわからないところがあれば教えてください!)
エラトステネスの篩と同じように、100以下の幸運数を求めることにしましょう。
まず、1は幸運数となります。

次に、1〜100までの数列の中で、2n番目の数(= 2番目, 4番目, 6番目, ... )をチェックしていきます。
画像の黄色い部分が2n番目の数

チェックした数は削除します。このとき、1の次の数である3は幸運数になります。

(赤数字は、幸運数であることが確定した数を指します)
次に、残っている数たちによる数列の中で、3n番目の数をチェックしていきます。すでに削除した数についてはカウントをしません。そこは注意が必要です。
画像の黄色い部分(5, 11, ..., 95)が3n番目の数
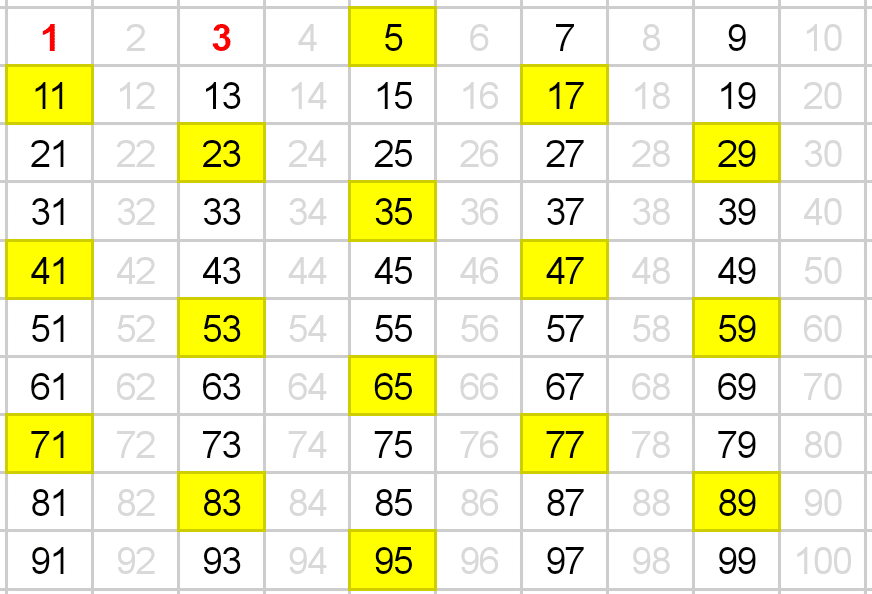
同じように、チェックした数を削除します。このとき、3の次の数である7は幸運数になります。

以下同様に、残った数列の中で「幸運数に決定した数の倍数」番目を削除していきます。
残っている数たちによる数列の中で、7n番目の数をチェック。
(すでに削除した数はカウントしません)
画像の黄色い部分(19, 39, 61, 81)が7n番目の数↓

チェックした数たちを削除。7の次の数である9が幸運数となる。

次に、残っている数たちによる数列の中で、9n番目の数をチェック。
(すでに削除した数はカウントしない)
画像の黄色い部分(27, 57, 91)が9n番目の数↓
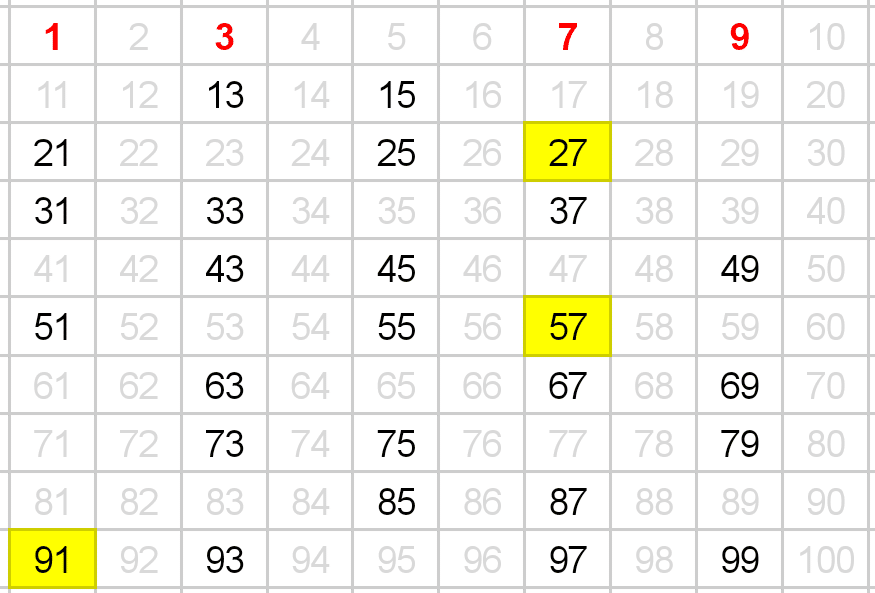
チェックした数たちを削除。9の次の数である13が幸運数となる。

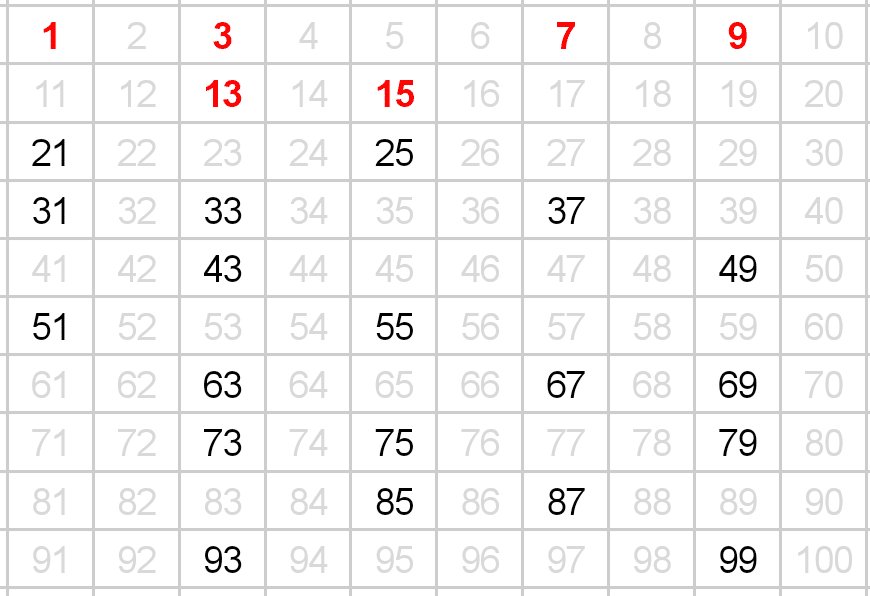
次に、残っている数たちによる数列の中で、13n番目の数をチェック。
(すでに削除した数はカウントしない)
画像の黄色い部分(45, 97)が13n番目の数↓

チェックした数たちを削除。13の次の数である15が幸運数となる。
次に、残っている数たちによる数列の中で、15n番目の数をチェック。
(すでに削除した数はカウントしない)
画像の黄色い部分(55)が15n番目の数↓
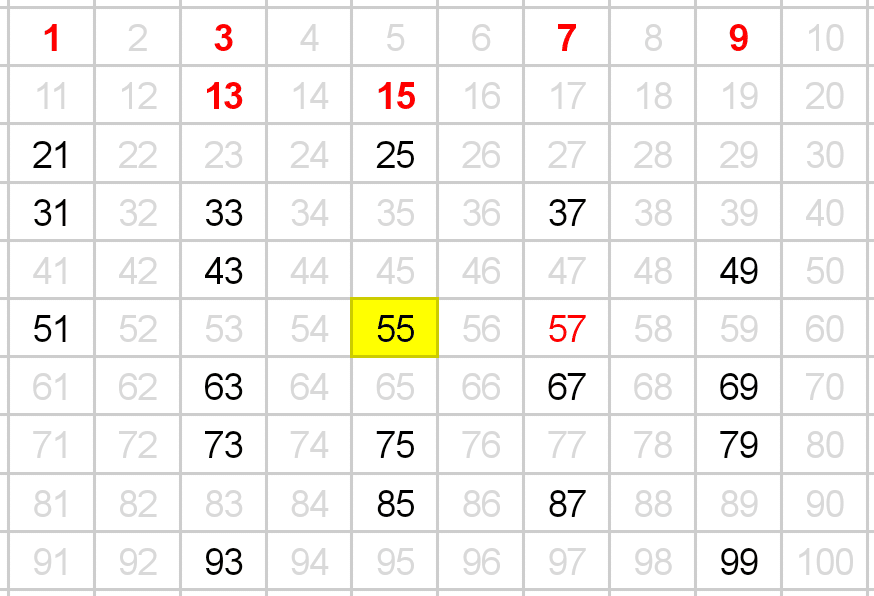
チェックした数たちを削除。15の次の数である21が幸運数となる。

次に、残っている数たちによる数列の中で、21n番目の数をチェック。
(すでに削除した数はカウントしない)
画像の黄色い部分(85)が21n番目の数↓

チェックした数たちを削除。21の次の数である25が幸運数となる。

次に、残っている数たちによる数列の中で、25n番目の数をチェックするのですが、100以下で残っている数は23個しかないので、これ以上数字を削除できません。
よって、残っている数たちはすべて幸運数となります。これが、100以下の幸運数です。

すごく丁寧に工程を書いてみましたが、わかりましたか?大きい幸運数を求める際は、この作業をもっと繰り返します。面倒ですが、やってみると面白いかもしれません。
あと、プログラミングができる方は実装してみてください。意外と複雑です😅
さて、幸運数を求めてみましたが、その中には素数も含まれています。
幸運数でかつ素数である数のことを「幸運素数」と言います。英語だと、Lucky Primeです。
最初の小さい幸運素数は以下の通りです。
3, 7, 13, 31, 37, 43, 67, 73, 79, 127, 151, 163, ...
すごく珍しいというわけではないですかね。僕の調べによると、10000以下の幸運素数は211個あります。
ちなみに、10000以下の素数は1229個。6個に1個くらいは幸運素数のようです。
さてさて、そもそもなぜ「幸運数」という名前なのでしょうか。
以下の「ニッセイ基礎研究所」様のサイトによると、1956年のGardiner、Lazarus、Metropolis、Ulamの論文がきっかけだそう。「ジョセフス問題」という問題と関わりがあるみたいですが、嬉しい幸運という感じではないですね…笑。
(詳しくはリンクをどうぞ)
いかがでしたか?
少し前には「ハッピー数」についても紹介しましたが、
個性的な名前の数が多いですね。他にも色々な数があるので、このnoteでも少しずつ紹介できればと思います。
このnoteを読んだ方に幸運が訪れますように。素数はいつも、あなたのそばに。
Let's enjoy SOSU !
最後まで読んでいただき、ありがとうございました。
