【塗り数字-23】Let's make SOSU !
 今回は、塗り数字の第22弾!数字を塗って素数を作るゲームです。
今回は、塗り数字の第22弾!数字を塗って素数を作るゲームです。 今回は前回と逆で、7が5個並んだあとに3が5個並んでいます。果たして、この中に素数はどれくらいあるのでしょうか…?
今回は前回と逆で、7が5個並んだあとに3が5個並んでいます。果たして、この中に素数はどれくらいあるのでしょうか…? 前回と同様、1桁の素数ですべての数字をカラフルに塗れますね。2桁以上の素数だとどうなるのか、考えてみてください。
前回と同様、1桁の素数ですべての数字をカラフルに塗れますね。2桁以上の素数だとどうなるのか、考えてみてください。






 まずは、2桁。73は素数。ひっくり返した37も素数です。
まずは、2桁。73は素数。ひっくり返した37も素数です。 3桁だと、733は素数。こちらも、数字をひっくり返した337も素数です。エマープですね。
3桁だと、733は素数。こちらも、数字をひっくり返した337も素数です。エマープですね。 773も素数。こちらは、377が素数ではない(=19×23)のでエマープではありません。
773も素数。こちらは、377が素数ではない(=19×23)のでエマープではありません。 四桁だと7333が素数。
四桁だと7333が素数。 5桁だと、73333が素数。3が多いですね。
5桁だと、73333が素数。3が多いですね。 77773も素数。今度は反対に、7が多数派です。
77773も素数。今度は反対に、7が多数派です。 と思ったら、6桁の733333は3が多数派。偏ってますね笑。これが、塗ることができる最大の素数です。
と思ったら、6桁の733333は3が多数派。偏ってますね笑。これが、塗ることができる最大の素数です。 最後に、惜しくも素数ではない合成数を紹介します。素因数分解、なかなか難しいですね…。
最後に、惜しくも素数ではない合成数を紹介します。素因数分解、なかなか難しいですね…。 73333=13×5641
73333=13×5641 77333=17×4549
77333=17×4549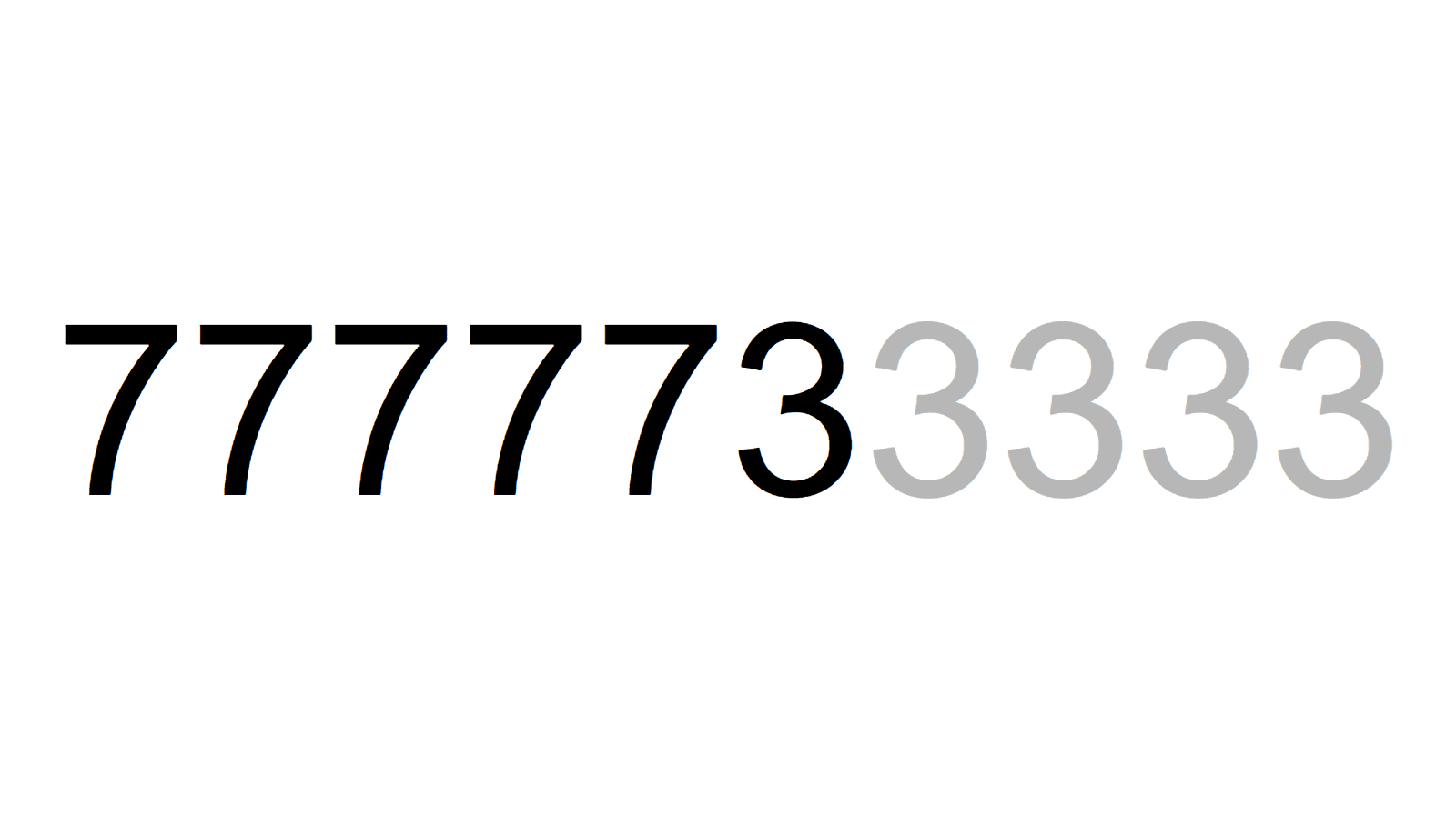 777773=709×1097
777773=709×1097 7733333=37×47×4447
7733333=37×47×4447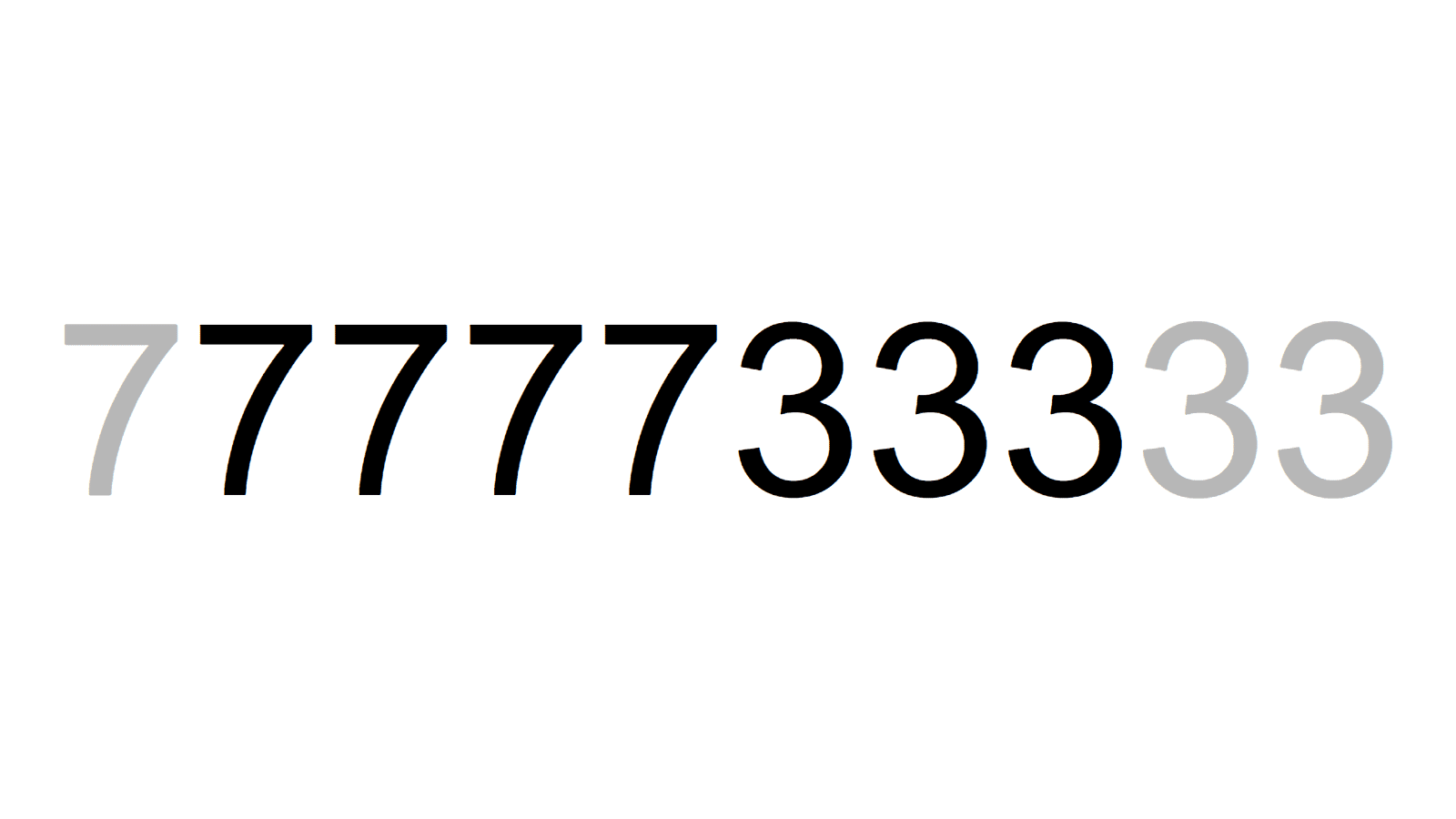 7777333=821×9473
7777333=821×9473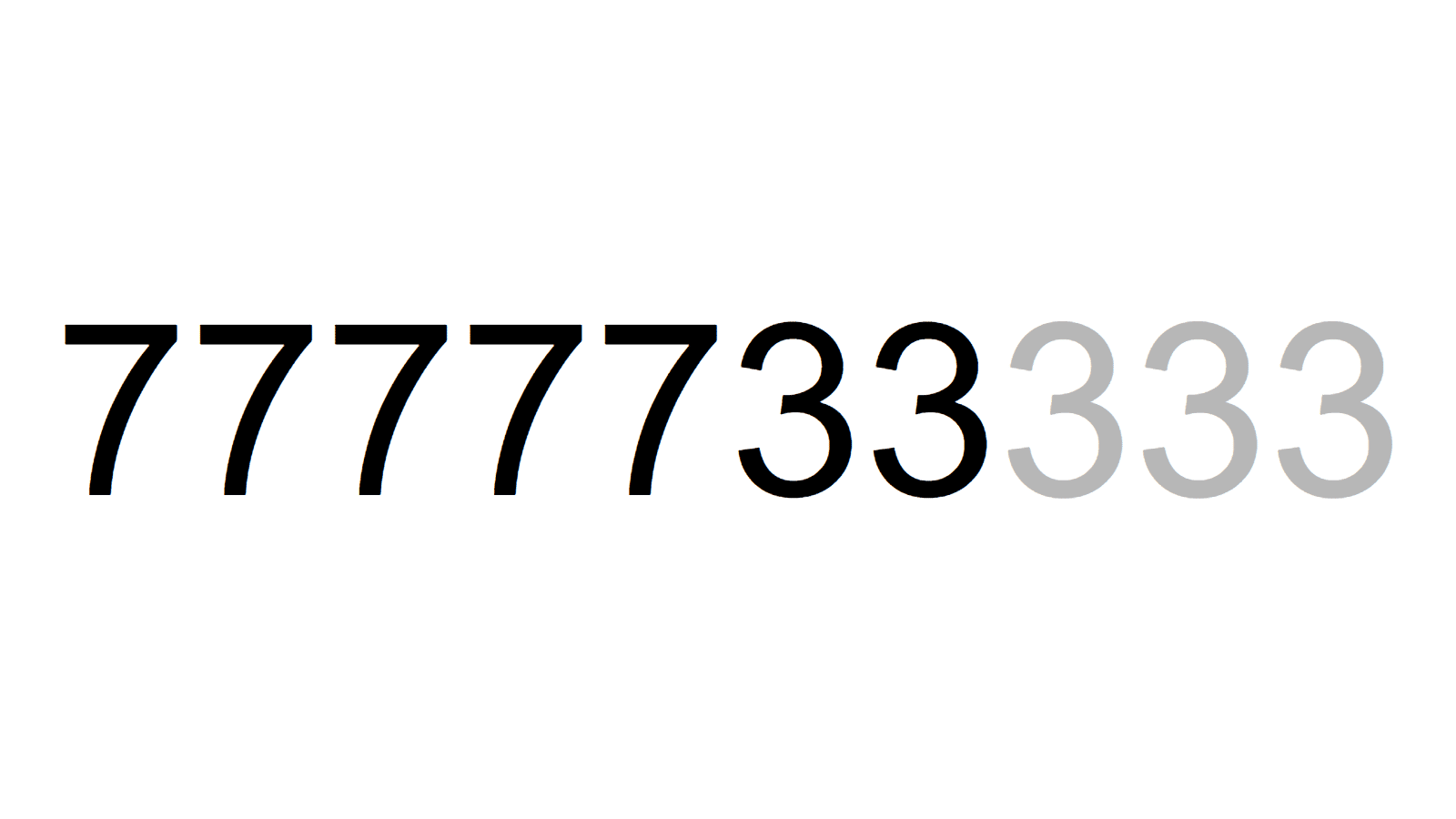 7777733=37×210209
7777733=37×210209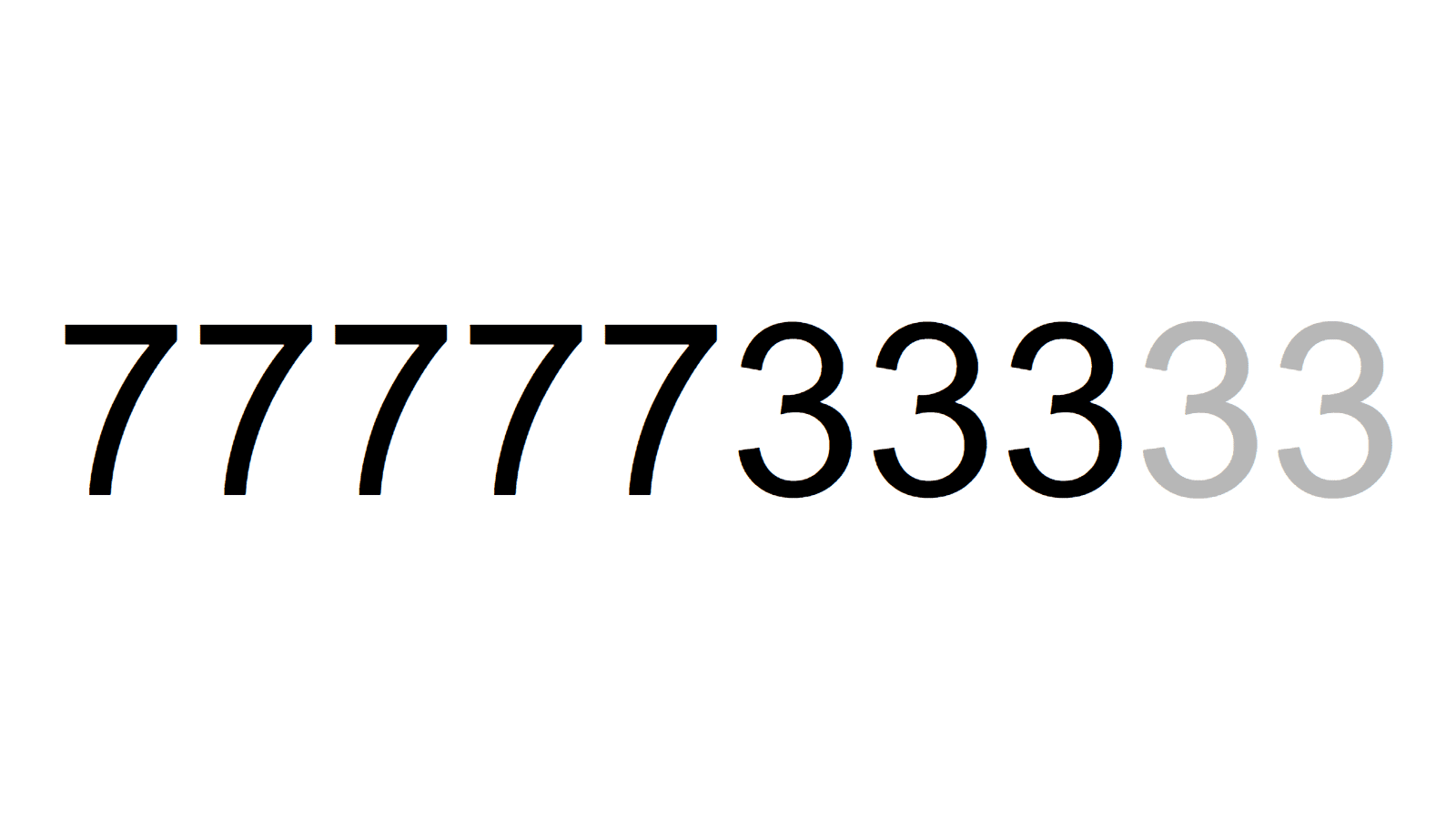 77777333=29×811×3307
77777333=29×811×3307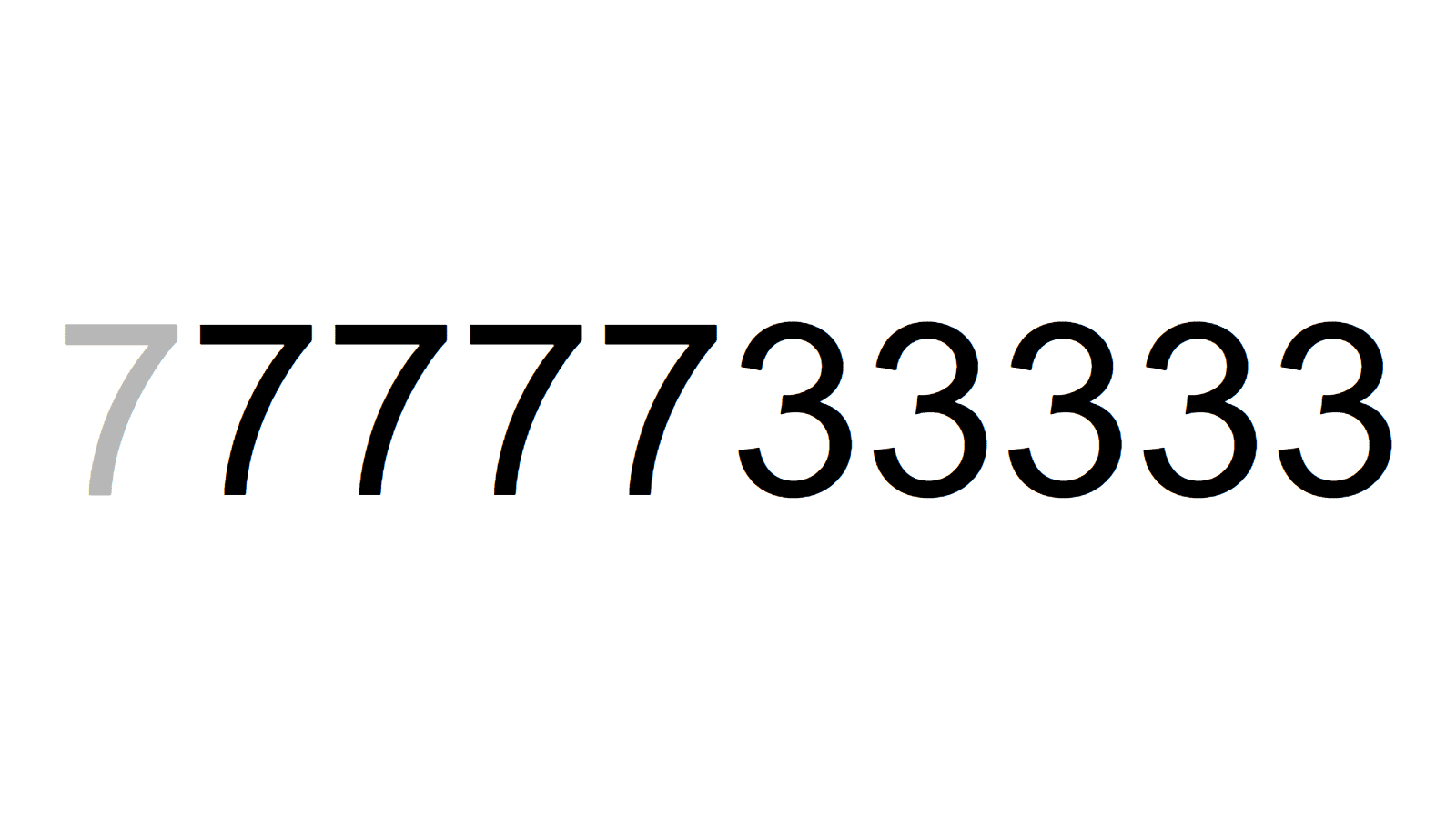 777733333=13×59825641
777733333=13×59825641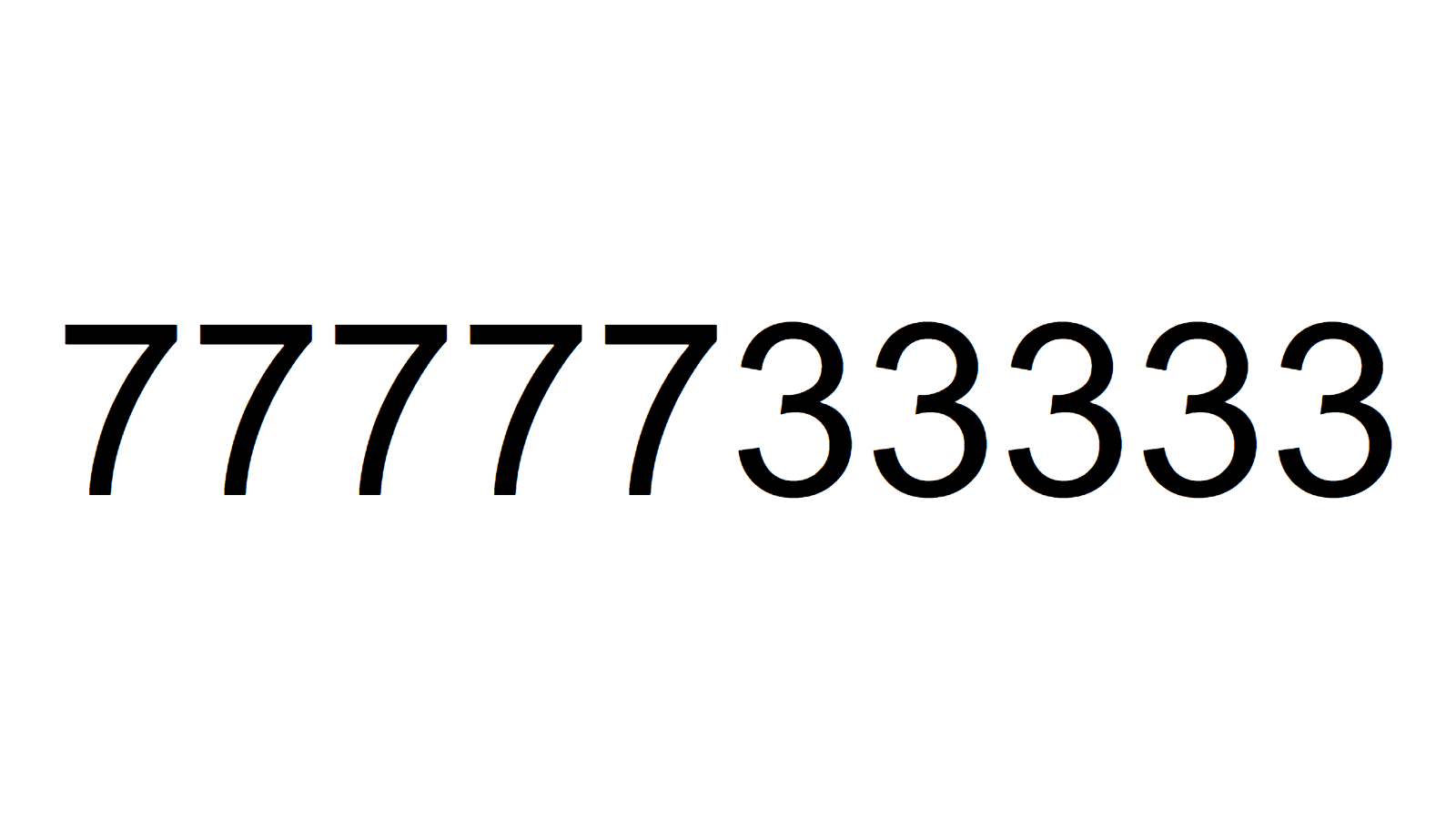 7777733333=37×41×271×18919
7777733333=37×41×271×18919