
【分数型】ワグスタッフ素数とは? Wagstaff prime
素数は自然数に含まれており、自然数は整数に含まれています。

しかし奇妙なことに、分数で表される素数もあります。それが今回紹介する、『ワグスタッフ素数』です。
以下のような形をした素数pのことをいいます。

qには素数が入りますが、そもそもqが偶数だと整数にはなりません。小さい数で試してみると、
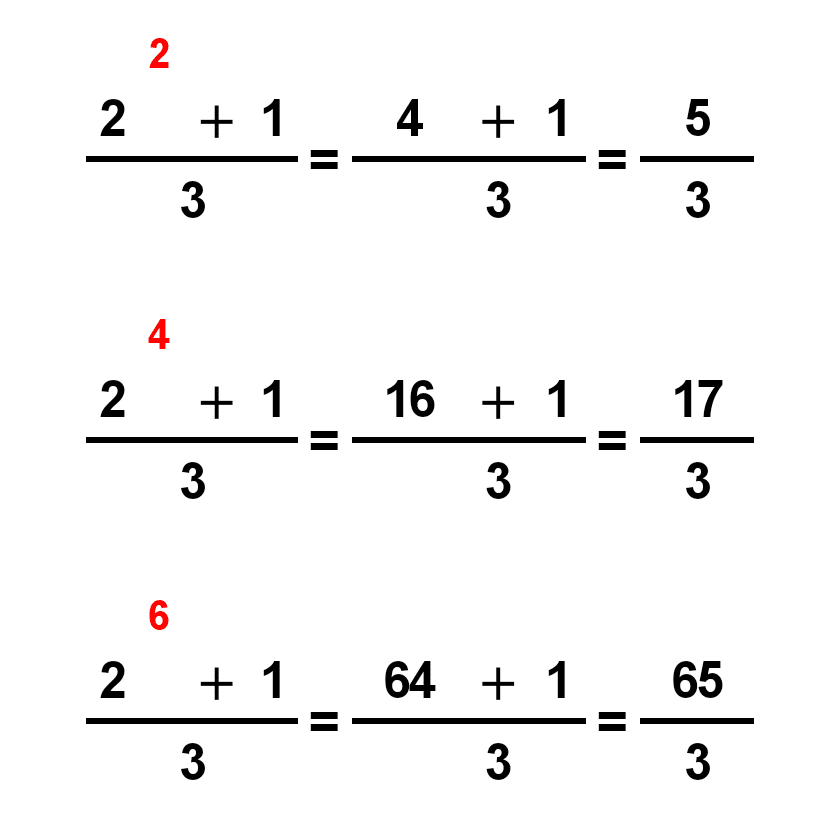
これは、2の「偶数乗」を3で割った余りが必ず1になるからです。ここでは登場しませんが、合同式を使うと上手く示せます。
逆に「奇数乗」であれば、3で割った余りは必ず2になります。よって、2^q + 1は3の倍数となって整数になるのです。
さて、ワグスタッフ素数の例をいくつか挙げてみましょう。10000以下のワグスタッフ素数は以下の通りです。


3, 5, 7, 11, 13と連続した素数を使ってワグスタッフ素数ができていますね。ただし、素数を入れれば必ず素数になるというわけではありません。
Wikipediaによると、
ワグスタッフ素数になるときの素数qは
3, 5, 7, 11, 13, 17, 19, 23, 31, 43, 61, 79, 101, ...
と続いています。q = 29, 37, 41などは素数にならないのです。
q = 29のとき、
(2^29 + 1)/3 = 178956971=59×3033169
q = 37
(2^37 + 1)/ 3 = 45812984491=1777×25781083
尚、qが素数でない場合、
(2^q + 1)/3
が素数になることは絶対にありません。これは後日詳しく説明してみたいなと思っています。
さて、ワグスタッフ素数という数はどうして考えられたのでしょうか?
こちらもWikipediaによると、
数学者のサミュエルS. ワグスタッフ・ジュニアという方から名付けられたそう。『ワグスタッフ』って人の名前なんですね!
また、ワグスタッフ素数は『新メルセンヌ予想』というものに関連しており、暗号理論との結びつきもあるようです。ただ、詳しい内容は理解していないので、ここでは省略します。興味のある方は調べてみてください。
いかがでしたか?
ワグスタッフ素数という、『分数型』の素数もあるというのは面白いです。他にも『○○素数』と呼ばれる数はあるので、少しずつ紹介していければと思っています。
素数はいつも、あなたのそばに。
Let's enjoy SOSU !
最後まで読んでいただき、ありがとうございました。
