
【オリジナル】大きい"digital erauqs"に関する考察
昨日、このようなツイートをしました。
629
— SOSU Lover (@SOSULover) June 29, 2022
ひっくり返すと
629#6月29日 pic.twitter.com/pTPwgOBmml
複数画像があるので見えにくいですが、「629」というデジタル数字を上下にひっくり返しても「629」になっているのです。

これをひっくり返すと

たしかに629のままですね。
これ、以前「平方数」について同じようなことを考えたことがありました。
筆者が勝手に「digital erauqs(デジタル・エラウクス)」と名付けました。そもそも、「erauqs」とは「square」を逆にしたもので、数字を逆順にしても平方数になる数のことを筆者は「erauqs」と呼んだのです。
そこで今回は、「digital erauqs」になる数を列挙してみようと思います。
ただし、下の方の桁が「0」で並んでいる場合は除くことにします。例えば、「10000と1」みたいなペアはカウントしません。
それではご覧ください!
画像に登場する2ですが、厳密にはデジタル数字ではありません。飾りが付いていますが、予めご了承ください。
3桁
まずは3桁。以前紹介したものもありますが、改めて紹介しておきましょう。
121
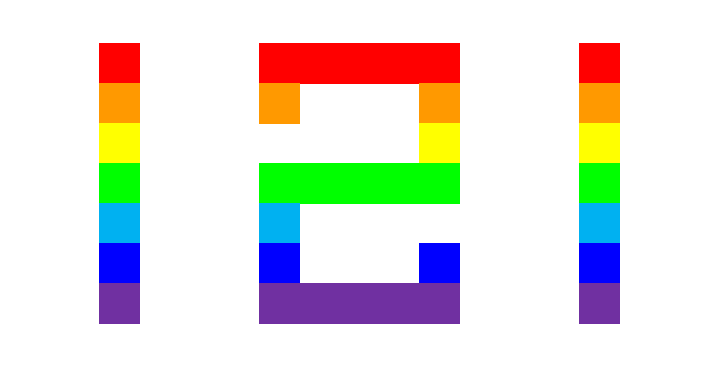

169, 961


529, 625


4桁
ここからは初紹介の数たちです。
6889


4桁は6889だけでした。意外とないものなんですね。
5桁
次に5桁です。
10201


69169


どちらも、ひっくり返しても同じ数になりますね。
さらに、どちらも「素数の2乗」になっています。先ほどの4桁の「6889=83×83」も「素数の2乗」でしたね!これはただの偶然なのでしょうか…?
6桁
6桁で該当するものはありませんでした。(688900, 6889)というペアもありますが、こちらは4桁で登場したものとほぼ同じなので除外しています。
7桁
1002001


1022121, 1212201


5221225

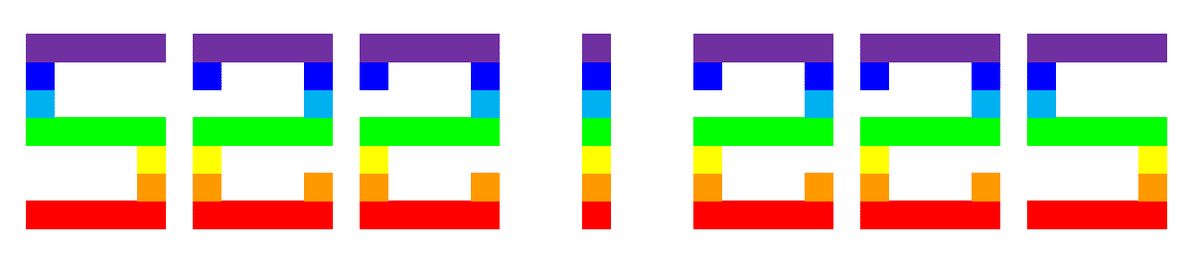
大きい桁でも、ちらほらあるようですね。先ほどの「素数の2乗」というのは偶然だったようです。
8桁
8桁で該当するものはありませんでした。
9桁
画像がたくさん出てきたので、ここでは数字のみ紹介します。
100020001
100020001=10001×10001
100220121, 1210022001
100220121=10011×10011
121022001=11001×11001
109181601
109181601=10449×10449
522808225
522808225=22865×22865
602555209
602555209=24547×24547
0と1だけの数字もあれば、そうでないものもあります。回文になっている平方数も意外とあるんだなーと思いました。
というわけで、長々と見てきました。奇数桁のdigital erauqsは多いですが、偶数桁はほとんどありません。これ、面白い特徴ですよね。もっと大きい桁だとどうなるのでしょうか…?
今回は、大きい桁にも注目してdigital erauqsを考えてみました。めちゃくちゃマニアックな内容になってしまいましたね…。筆者はこういう「かずあそび」が大好きなので、これからも自由な発想を駆使して色々と考えていこうと思います。
素数はいつも、あなたのそばに。
Let's enjoy SOSU !
最後まで読んでいただき、ありがとうございました。
