Bias corrected accelerated bootstrap法による信頼区間(Python)
パーセンタイル法
パーセンタイル法は、ブートストラップ信頼区間を求める最も基本的な方法である。例えば95%信頼区間を求める場合、ブートストラップ標本から得られた統計量を小さい順に並べ、2.5パーセンタイルと97.5パーセンタイルの値を信頼区間の下限と上限とする方法である。
利点としては、単純で実装がしやすいこと。
Bias-Corrected and Accelerated bootstrap(BCa)法
BCa法は、パーセンタイル法を改良した、より精度の高い信頼区間の計算方法である。バイアスの補正(Bias-Correction)と加速度(Acceleration)の調整を行うことが特徴である。では、それぞれ詳しく見ていきます。
バイアスの補正(Bias-Correction)
BCa法がより有効になるように、今回は非対称な分布を持つデータを使用する。元データからブーストラップサンプルを作成し、統計量(今回は平均値)を求める。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 非対称な分布を持つデータ
salary_data = np.array([320, 350, 380, 400, 420, 450, 480, 500, 550, 600,
650, 700, 800, 900, 1200, 1600])
# 平均値の計算
observed_mean = np.mean(salary_data)
# ブートストラップを実行(1000回)
n_bootstrap = 1000
bootstrap_means = np.zeros(n_bootstrap)
for i in range(n_bootstrap):
bootstrap_sample = np.random.choice(salary_data, size=len(salary_data),
replace=True)
bootstrap_means[i] = np.mean(bootstrap_sample)元データの平均値(observed_mean)とブーストラップサンプルの平均値(bootstrap_means)からバイアス補正係数を計算する。
# バイアス補正係数z0の計算
prop_less = np.mean(bootstrap_means < observed_mean)
z0 = stats.norm.ppf(prop_less)加速度(Acceleration)の調整
理屈はよくわからないが、下のような計算をしている。
# ジャックナイフ推定値を計算
n = len(salary_data)
jack_values = np.zeros(n)
for i in range(n):
jack_sample = np.delete(salary_data, i)
jack_values[i] = np.mean(jack_sample)
# 加速度係数を計算
jack_mean = np.mean(jack_values)
numerator = np.sum((jack_mean - jack_values) ** 3)
denominator = 6 * (np.sum((jack_mean - jack_values) ** 2)) ** 1.5
a = numerator / denominatorBCa法による信頼区間の算出
バイアス補正係数と加速度係数からBCa補正された信頼区間を算出する。
# 信頼区間の確率点を計算
z_alpha = stats.norm.ppf([0.025, 0.975])
# BCa補正された確率点を計算
percentiles = np.zeros(2)
for i in range(2):
numerator = z0 + z_alpha[i]
denominator = 1 - a * numerator
percentile = stats.norm.cdf(z0 + numerator/denominator)
percentiles[i] = percentile * 100
# 信頼区間を計算
confidence_interval = np.percentile(bootstrap_means, percentiles)
print(f"95%信頼区間: {confidence_interval[0]:.1f} - {confidence_interval[1]:.1f}")95%信頼区間: 527.1 - 870.1
Bca法によるバイアス補正が必要な理由
例として右に裾の長い給与データを使用する(高給与者が少数いる)。
# 非対称な分布を持つ給与データ
salary_data = np.array([320, 350, 380, 400, 420, 450, 480, 500, 550, 600,
650, 700, 800, 900, 1200, 1600])このような分布のデータでは、ブーストラップサンプルにて高給与者のデータが含まれるか否かで、平均値が大きく変動する。今回の場合は、ブーストラップサンプルの平均値が元データの平均値よりも小さくなりやすい。
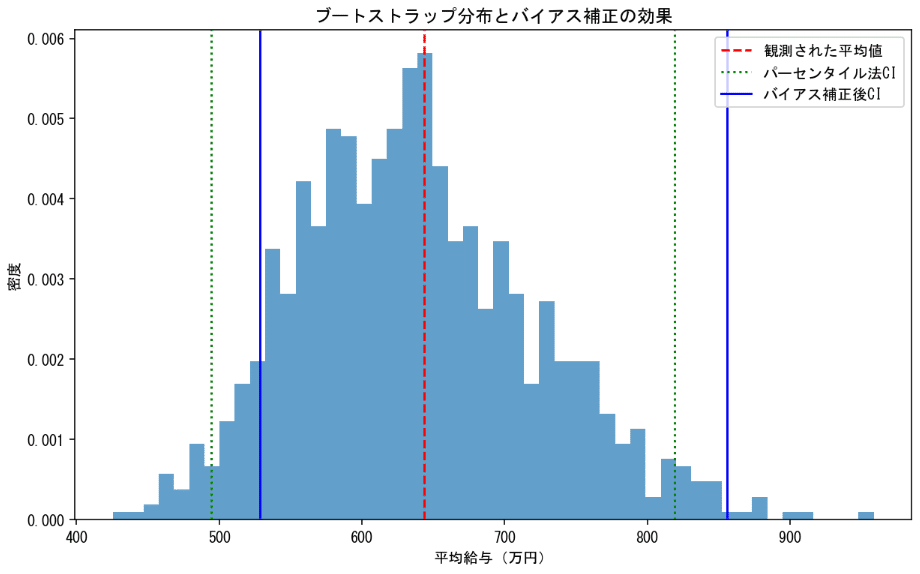
バイアス補正の効果を視覚的に理解するため、ブートストラップ分布をプロットする。
# 平均値の計算
observed_mean = np.mean(salary_data)
# ブートストラップを実行(1000回)
n_bootstrap = 1000
bootstrap_means = np.zeros(n_bootstrap)
for i in range(n_bootstrap):
bootstrap_sample = np.random.choice(salary_data, size=len(salary_data),
replace=True)
bootstrap_means[i] = np.mean(bootstrap_sample)
# バイアス補正係数z0の計算
prop_less = np.mean(bootstrap_means < observed_mean)#元データの平均値よりも小さいブーストラップサンプル平均値の割合
z0 = stats.norm.ppf(prop_less)
# 通常の95%信頼区間(パーセンタイル法)
normal_ci = np.percentile(bootstrap_means, [2.5, 97.5])
# バイアス補正後の確率点を計算
z_alpha = stats.norm.ppf([0.025, 0.975]) # 95%信頼区間用の正規分布の分位点
adjusted_percentiles = stats.norm.cdf(z0 + 2*z0 + z_alpha) * 100
bias_corrected_ci = np.percentile(bootstrap_means, adjusted_percentiles)
plt.figure(figsize=(10, 6))
plt.hist(bootstrap_means, bins=50, density=True, alpha=0.7)
plt.axvline(observed_mean, color='red', linestyle='--',
label='観測された平均値')
plt.axvline(normal_ci[0], color='green', linestyle=':',
label='パーセンタイル法CI')
plt.axvline(normal_ci[1], color='green', linestyle=':')
plt.axvline(bias_corrected_ci[0], color='blue', linestyle='-',
label='バイアス補正後CI')
plt.axvline(bias_corrected_ci[1], color='blue', linestyle='-')
plt.xlabel('平均給与(万円)')
plt.ylabel('密度')
plt.legend()
plt.title('ブートストラップ分布とバイアス補正の効果')
plt.show()バイアスの補正されていないパーセンタイル法では、ブーストラップサンプルの平均値が元データの平均値よりも小さくなりやすい。これは、サンプリングの際に、1200や1600が抽出されるかどうかで平均値が大きく動きやすいことが影響している。これを補正するのがBCa法である。
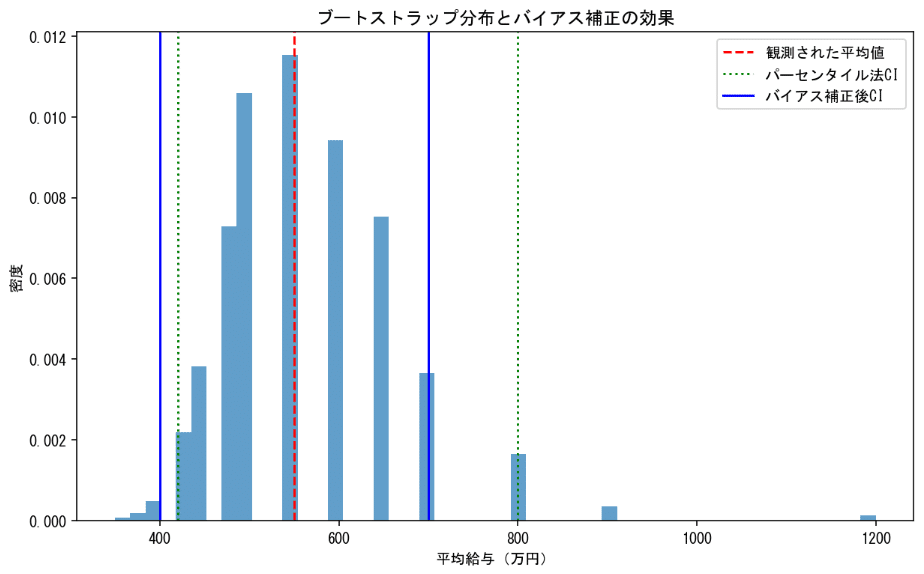
逆に、極端な外れ値が存在する場合は注意が必要である。上の給与データに1億の給与者を加えると分布は以下の通りとなる。外れ値によって、信頼区間が右に引き伸ばされている。

実際のデータ分析では、外れ値には何かしらの対応が必要となる。例としては以下のものがあげられる。
外れ値の検出と処理
平均値の代わりに中央値を使用
上記の外れ値が存在するデータにて、平均値の代わりに中央値を使用すると以下のようになる。
まとめ
加速度について理論的なことはよくわからないが、実装するのは難しくなさそう。ただ、極端な外れ値が存在するときは、それに引っ張られるため注意が必要である。
